给定二维平面整数点集输出“最大点集”算法（今日头条面试题）

Posted 2021-01-03 tangzhenqiang

引子

最近自己的独立游戏上线了，算是了却了一桩心愿。接下来还是想找一份工作继续干，创业的事有缘再说。

找工作之前，总是要浏览一些实战题目，热热身嘛。通过搜索引擎，搜到了今日头条的一道面试题。

题目

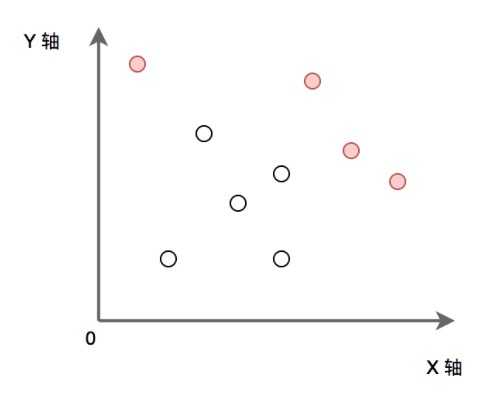
P为给定的二维平面整数点集。定义 P 中某点x，如果x满足 P 中任意点都不在 x 的右上方区域内（横纵坐标都大于x），则称其为“最大的”。求出所有“最大的”点的集合。（所有点的横坐标和纵坐标都不重复, 坐标轴范围在[0, 1e9) 内）

如下图：实心点为满足条件的点的集合。请实现代码找到集合 P 中的所有 ”最大“ 点的集合并输出。

输入描述:

第一行输入点集的个数 N， 接下来 N 行，每行两个数字代表点的 X 轴和 Y 轴。

输出描述:

输出“最大的” 点集合， 按照 X 轴从小到大的方式输出，每行两个数字分别代表点的 X 轴和 Y轴。

输入例子1:

5
1 2
5 3
4 6
7 5
9 0

输出例子1:

4 6
7 5
9 0

 思路

1.暴力搜索法

先取一点，然后和其他所有点比较，看看是否有点在其右上方，没有则证明该点是“最大点”。重复检测所有的点。显而易见，算法的复杂度为O(n²)

2.变治法（预排序）

由“最大点”的性质可知，对于每一个“最大点”，若存在其他点的y值大于该点y值，那么其他点x值必然小于该点的x值。

换言之，当某一点确定它的x值高于所有y值大于它的点的x值，那么该点就是“最大点” 。网上给出的答案基本上都是这个套路。

对于y有序的点集，只需要O(n)即可输出“最大点”点集。一般基于比较的排序算法时间复杂度O(nlogn)。那么，显而易见，算法整体复杂度为O(nlogn)。

3.变治法（过滤+预排序）

过滤很简单，就是在集合中找出一个比较好的点，然后过滤掉其左下角的所有点。然后再采用方法2对过滤后的点集求解。

那么这个集合中比较好的点，怎么找，或者说哪个点是比较好的点。显而易见，越靠近点集右上角的点，左下角的面积就越大，越可以过滤更多的点，故越好。

儿时学过，两个数的和一定，那么两数差越小，乘积越大。简单设计，该点x和y的和减去x和y差的绝对值越大，该点越好。

 

对比实现

#include<iostream>
#include<algorithm>
#include<vector>
#include <cstdlib>
#include <ctime>
using namespace std;
struct point{     //定义结构体
    int x,y;
};
bool cmp(point a,point b){  //自定义排序方法
    return a.y==b.y?a.x>b.x:a.y<b.y;  //y升序，x降序
}
int main(){
    clock_t start,finish;
    double totaltime;
    std::srand(std::time(nullptr)); // use current time as seed for random generator
    int count;  
    cout<<"输入点的个数和点：" ;
    cin>>count;
    vector<point> p; //容器用来装平面上的点
    for(int i=0;i<count;i++){
        point temp;
        temp.x = std::rand()% 100000000;
        temp.y = std::rand()% 100000000;
        p.push_back(temp); //为了方便对比性能，我们随机插入大量点
    }
    start = clock();
    vector<point> filter;//定义过滤容器
    vector<point> res;  //定义结果容器
    int curMaxRank = 0;
    int curMaxIndex = 0;
    for(int i=0;i<count;i++){
        int temp =p[i].x+p[i].y-std::abs(p[i].x-p[i].y);
        if(temp > curMaxRank)
        {
            curMaxRank = temp;
            curMaxIndex = i;
        }
    }
    for(int i=0;i<count;i++)
    {
        if(p[i].x >= p[curMaxIndex].x || p[i].y>= p[curMaxIndex].y)
        {
            filter.push_back(p[i]);
        }
    }
    
    sort(filter.begin(),filter.end(),cmp);
    res.push_back(filter[filter.size()-1]);  //左上角的那个点，一定符合条件
    int maxx=filter[filter.size()-1].x;
    for(int i=filter.size()-2;i>=0;i--){  //y从大到小，若i点x值大于所有比其y值大的点的x值，那么i点为“最大点”。
        if(filter[i].x>maxx){
            res.push_back(filter[i]);
            maxx=filter[i].x;
        }
    }
    finish = clock();
    cout<<"过滤后点数量："<<filter.size()<<endl;
    cout<<"符合条件的点数量："<<res.size()<<endl;
    for(int i=0;i<res.size();i++){
        printf("%d %d
", res[i].x, res[i].y);
    }
    totaltime=(double)(finish-start)/CLOCKS_PER_SEC;
    cout<<"
此程序的运行时间为"<<totaltime<<"秒！"<<endl;
    cout<<"------------------------------------------------"<<endl;
    start = clock();
    sort(p.begin(),p.end(),cmp); 
    res.clear();
    res.push_back(p[p.size()-1]);  //左上角的那个点，一定符合条件
    int maxX=p[p.size()-1].x;
    for(int i=p.size()-2;i>=0;i--){  
        //y从大到小，若i点x值大于所有比其y值大的点的x值，那么i点为“最大点”。
        if(p[i].x>maxX){
            res.push_back(p[i]);
            maxX=p[i].x;
        }
    }
    finish = clock();
    cout<<"符合条件的点数量："<<res.size()<<endl;
    for(int i=0;i<res.size();i++){
        printf("%d %d
", res[i].x, res[i].y);
    }
    totaltime=(double)(finish-start)/CLOCKS_PER_SEC;
    cout<<"
此程序的运行时间为"<<totaltime<<"秒！"<<endl;
    
    return 0;
} 

实际实验数据，输入点数为500000

过滤后点数量：210
符合条件的点数量：13
27952428 99999996
37918705 99999707
91085697 99998621
91655748 99997454
92150806 99996701
93153071 99993113
98057931 99989335
98932694 99986718
99589255 99982487
99986370 99972489
99998853 98880028
99999099 96104043
99999964 57986619

此程序的运行时间为0.020495秒！
------------------------------------------------
符合条件的点数量：13
27952428 99999996
37918705 99999707
91085697 99998621
91655748 99997454
92150806 99996701
93153071 99993113
98057931 99989335
98932694 99986718
99589255 99982487
99986370 99972489
99998853 98880028
99999099 96104043
99999964 57986619

此程序的运行时间为0.309453秒！

总结与展望

对于随机点进行大量测试，发现存在笔者给出的过滤方法，平均可以过滤99.9%的点。也就是说过滤后所剩点m的数量为原始点集n数量的千分之一。

使用过滤的额外好处是，我们只需要开辟千分之一的内存，然后就可以不改变原有点集的顺序，也就是说如果题目还有不改变原有点集的要求，依然可以满足 。

过滤付出的时间代价是线性的。那么算法的整体复杂度为O(n+ mlogm)，而一般m值为n的千分之一。那么算法的平均复杂度为O(n)，空间复杂度O(m)。通过上述代码实际对比，性能提高了大约20倍左右。

使用O(m)空间，可以确保不改变原有点集的顺序。 可不可以继续优化，可以可以，优化永无止境，只要别轻易放弃思考。

 

如果对你有所帮助，点个赞呗~  原创文章，请勿转载，谢谢