强化学习

Posted 2021-01-02 xiaofanke

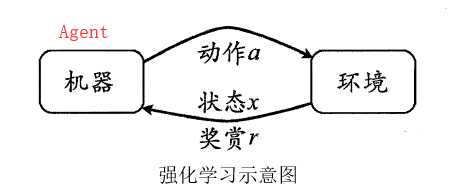
强化学习：是智能体（Agent）以“试错”的方式进行学习，通过与环境进行交互获得的奖赏指导行为，目标是使智能体获得最大的奖赏。(来源百度百科) 强化学习的指导信息很少，而且往往是在事后（最后一个状态）才给出的，这就导致了一个问题，就是获得正回报或者负回报以后，如何将回报分配给前面的状态。

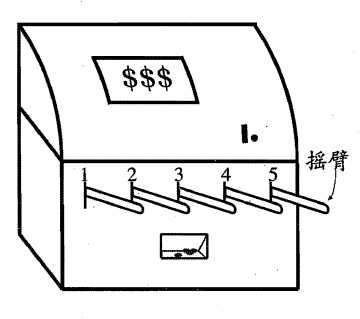
1.K-摇臂赌博机

强化学习的最终奖赏是在多步动作之后才能观察到，先考虑单步奖赏最大化（仅考虑一步操作），分成两步：①确定每个动作对应的奖赏②执行奖赏最大的动作

每个动作对应的奖赏可能是服从某个概率分布，所以对所有的动作遍历一次，无法确切得到每个动作对应的奖赏。

 K-摇臂赌博机 ，K-摇臂赌博机有K 个摇臂，赌徒在投入一个硬币后可选择按下其中」个摇臂，每个摇臂以一定的概率吐出硬币?但这个概率赌徒并不知道.赌徒的目标是通过一定的策略最大化自己的

奖赏，即获得最多的硬币.

为了获得每个摇杆的期望奖赏，则可采用"仅探索" 法:将所有的尝试机会平均分配给每个摇臂(即轮流按下每个摇臂)，最后以每个摇臂各自的平均吐币橄率作为其奖赏期望的近似估计.

若仅为执行奖赏最大的动作，则可采用"仅利用" 法:按下目前最优的(即到目前为止平均奖赏最大的)摇臂，若有多个摇臂同为最优，则从中随机选取一个.

显然，"仅探索"法能很好地估计每个摇臂的奖赏，却会失去很多选择最优摇臂的机会;"仅利用"法则相反，它没有很好地估计摇臂期望奖赏，很可能经常选不到最优摇臂.因此，这两种方法都难以使最终

的累积奖赏最大化.

为了讲累计奖赏最大化，需要载探索和利用之间找到一个合适的平衡：

显然第5步中的均匀分布随机选取并不合适，因为摇杆的平均奖赏高对应的选择概率应该高于其他摇杆（类似轮盘赌法）。所以提出

注：>0 称为"温度" , 越小则平均奖赏高的摇臂被选取的概率越高.趋于0 时Softmax 将趋于"仅利用"，趋于无穷大时Softmax 则将趋于"仅探索"。

 2 马尔科夫决策过程

一个马尔可夫决策过程由一个四元组构成M = (S, A, P_sa, ??) 

• S: 表示状态集(states)，有s∈S，s_i表示第i步的状态。
• A: 表示一组动作(actions)，有a∈A，a_i表示第i步的动作。
• ??_sa: 表示状态转移概率。??_s?? 表示的是在当前s ∈ S状态下，经过a ∈ A作用后，会转移到的其他状态的概率分布情况。比如，在状态s下执行动作a，转移到s‘的概率可以表示为p(s‘|s,a)。
• R: S×A?? ，R是回报函数(reward function)。有些回报函数状态S的函数，可以简化为R: S??。如果一组(s,a)转移到了下个状态s‘，那么回报函数可记为r(s‘|s, a)。如果(s,a)对应的下个状态s‘是唯一的，那么回报函数也可以记为r(s,a)。

MDP 的动态过程如下：某个智能体(agent)的初始状态为s₀，然后从 A 中挑选一个动作a₀执行，执行后，agent 按P_sa概率随机转移到了下一个s₁状态，s₁∈ P_s0a0。然后再执行一个动作a₁，就转移到了s₂，接下来再执行a₂…，我们可以用下面的图表示状态转移的过程。

状态函数V^π (x，a) 表示从状态x 出发, 使用策略π作所带来的累积奖赏；动作函数Q^π (x，a) 表示从状态x出发，执行动作a后再使用策略π带来的累积奖赏。

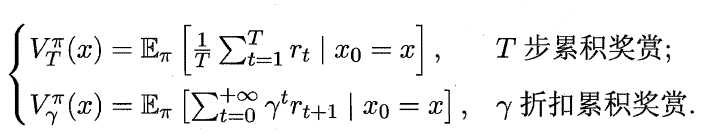
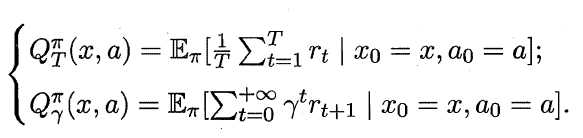
状态值函数和动作值函数展开后可得：

 

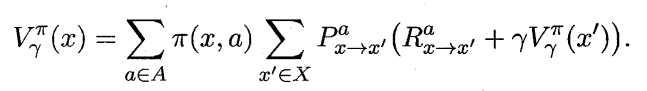
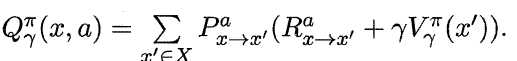
其中：
 所以：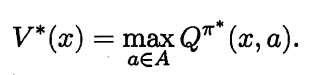

 

，

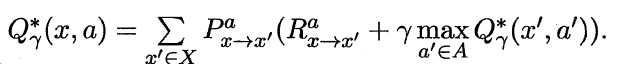
策略迭代：

值迭代：