一、前言
二值图像,顾名思义就是图像的亮度值只有两个状态:黑(0)和白(255)。二值图像在图像分析与识别中有着举足轻重的地位,因为其模式简单,对像素在空间上的关系有着极强的表现力。在实际应用中,很多图像的分析最终都转换为二值图像的分析,比如:医学图像分析、前景检测、字符识别,形状识别。二值化+数学形态学能解决很多计算机识别工程中目标提取的问题。
二值图像分析最重要的方法就是连通区域标记,它是所有二值图像分析的基础,它通过对二值图像中白色像素(目标)的标记,让每个单独的连通区域形成一个被标识的块,进一步的我们就可以获取这些块的轮廓、外接矩形、质心、不变矩等几何参数。
下面是一个二值图像被标记后,比较形象的显示效果,这就是我们这篇文章的目标。
二、连通域
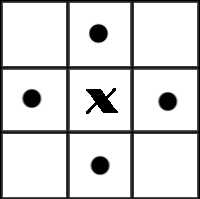
在我们讨论连通区域标记的算法之前,我们先要明确什么是连通区域,怎样的像素邻接关系构成连通。在图像中,最小的单位是像素,每个像素周围有8个邻接像素,常见的邻接关系有2种:4邻接与8邻接。4邻接一共4个点,即上下左右,如下左图所示。8邻接的点一共有8个,包括了对角线位置的点,如下右图所示。
如果像素点A与B邻接,我们称A与B连通,于是我们不加证明的有如下的结论:
如果A与B连通,B与C连通,则A与C连通。
在视觉上看来,彼此连通的点形成了一个区域,而不连通的点形成了不同的区域。这样的一个所有的点彼此连通点构成的集合,我们称为一个连通区域。
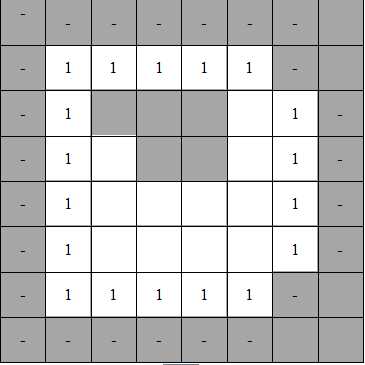
下面这符图中,如果考虑4邻接,则有3个连通区域;如果考虑8邻接,则有2个连通区域。(注:图像是被放大的效果,图像正方形实际只有4个像素)。
三、连通区域的标记
连通区域标记算法有很多种,有的算法可以一次遍历图像完成标记,有的则需要2次或更多次遍历图像。这也就造成了不同的算法时间效率的差别,在这里我们介绍2种算法。
第一种算法是现在matlab中连通区域标记函数bwlabel中使的算法,它一次遍历图像,并记下每一行(或列)中连续的团(run)和标记的等价对,然后通过等价对对原来的图像进行重新标记,这个算法是目前我尝试的几个中效率最高的一个,但是算法里用到了稀疏矩阵与Dulmage-Mendelsohn分解算法用来消除等价对,这部分原理比较麻烦,所以本文里将不介绍这个分解算法,取而代这的用图的深度优先遍历来替换等价对。
第二种算法是现在开源库cvBlob中使用的标记算法,它通过定位连通区域的内外轮廓来标记整个图像,这个算法的核心是轮廓的搜索算法,这个我们将在文章中详细介绍。这个算法相比与第一种方法效率上要低一些,但是在连通区域个数在100以内时,两者几乎无差别,当连通区域个数到了103103数量级时,上面的算法会比该算法快10倍以上。
四、基于行程的标记
我们首先给出算法的描述,然后再结合实际图像来说明算法的步骤。
1,逐行扫描图像,我们把每一行中连续的白色像素组成一个序列称为一个团(run),并记下它的起点start、它的终点end以及它所在的行号。
2,对于除了第一行外的所有行里的团,如果它与前一行中的所有团都没有重合区域,则给它一个新的标号;如果它仅与上一行中一个团有重合区域,则将上一行的那个团的标号赋给它;如果它与上一行的2个以上的团有重叠区域,则给当前团赋一个相连团的最小标号,并将上一行的这几个团的标记写入等价对,说明它们属于一类。
3,将等价对转换为等价序列,每一个序列需要给一相同的标号,因为它们都是等价的。从1开始,给每个等价序列一个标号。
4,遍历开始团的标记,查找等价序列,给予它们新的标记。
5,将每个团的标号填入标记图像中。
6,结束。
我们来结合一个三行的图像说明,上面的这些操作。
第一行,我们得到两个团:[2,6]和[10,13],同时给它们标记1和2。
第二行,我们又得到两个团:[6,7]和[9,10],但是它们都和上一行的团有重叠区域,所以用上一行的团标记,即1和2。
第三行,两个:[2,4]和[7,8]。[2,4]这个团与上一行没有重叠的团,所以给它一个新的记号为3;而[2,4]这个团与上一行的两个团都有重叠,所以给它一个两者中最小的标号,即1,然后将(1,2)写入等价对。
全部图像遍历结束,我们得到了很多个团的起始坐标,终止坐标,它们所在的行以及它们的标号。同时我们还得到了一个等价对的列表。
下面我们用C++实现上面的过程,即步骤2,分两个函数进行:
1)fillRunVectors函数完成所有团的查找与记录;
void fillRunVectors(const Mat& bwImage, int& NumberOfRuns, vector<int>& stRun, vector<int>& enRun, vector<int>& rowRun)
{
for (int i = 0; i < bwImage.rows; i++)
{
const uchar* rowData = bwImage.ptr<uchar>(i);
if (rowData[0] == 255)
{
NumberOfRuns++;
stRun.push_back(0);
rowRun.push_back(i);
}
for (int j = 1; j < bwImage.cols; j++)
{
if (rowData[j - 1] == 0 && rowData[j] == 255)
{
NumberOfRuns++;
stRun.push_back(j);
rowRun.push_back(i);
}
else if (rowData[j - 1] == 255 && rowData[j] == 0)
{
enRun.push_back(j - 1);
}
}
if (rowData[bwImage.cols - 1])
{
enRun.push_back(bwImage.cols - 1);
}
}
}
2)firstPass函数完成团的标记与等价对列表的生成。相比之下第二个函数要稍微难理解一些。
void firstPass(vector<int>& stRun, vector<int>& enRun, vector<int>& rowRun, int NumberOfRuns,vector<int>& runLabels, vector<pair<int, int>>& equivalences, int offset)
{
runLabels.assign(NumberOfRuns, 0);
int idxLabel = 1;
int curRowIdx = 0;
int firstRunOnCur = 0;
int firstRunOnPre = 0;
int lastRunOnPre = -1;
for (int i = 0; i < NumberOfRuns; i++)
{
if (rowRun[i] != curRowIdx)
{
curRowIdx = rowRun[i];
firstRunOnPre = firstRunOnCur;
lastRunOnPre = i - 1;
firstRunOnCur = i;
}
for (int j = firstRunOnPre; j <= lastRunOnPre; j++)
{
if (stRun[i] <= enRun[j] + offset && enRun[i] >= stRun[j] - offset && rowRun[i] == rowRun[j] + 1)
{
if (runLabels[i] == 0) // 没有被标号过
runLabels[i] = runLabels[j];
else if (runLabels[i] != runLabels[j])// 已经被标号
equivalences.push_back(make_pair(runLabels[i], runLabels[j])); // 保存等价对
}
}
if (runLabels[i] == 0) // 没有与前一列的任何run重合
{
runLabels[i] = idxLabel++;
}
}
}
接下来是我们的重点,即等价对的处理,我们需要将它转化为若干个等价序列。比如有如下等价对:
(1,2),(1,6),(3,7),(9-3),(8,1),(8,10),(11,5),(11,8),(11,12),(11,13),(11,14),(15,11)
我们需要得到最终序列是:
list1:list1:1-2-5-6-8-10-11-12-13-14-15
list2:list2:3-7-9
list3:list3:4
一个思路是将1-15个点都看成图的结点,而等价对(1,2)说明结点1与结点2之间有通路,而且形成的图是无向图,即(1,2)其实包含了(2,1)。我们需要遍历图,找出其中的所有连通图。所以我们采用了图像深入优先遍历的原理,进行等价序列的查找。
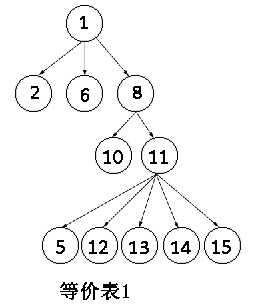
从结点1开始,它有3个路径1-2,1-6,1-8。2和6后面都没有路径,8有2条路径通往10和11,而10没有后续路径,11则有5条路径通往5,12,13,14,15。等价表1查找完毕。
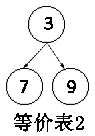
第2条等价表从3开始,则只有2条路径通向7和9,7和9后面无路径,等价表2查找完毕。
最后只剩下4,它没有在等价对里出现过,所以单儿形成一个序列(这里假设步骤2中团的最大标号为15)。
下面是这个过程的C++实现,每个等价表用一个vector<int>来保存,等价对列表保存在map<pair<int,int>>里。
void replaceSameLabel(vector<int>& runLabels, vector<pair<int, int>>&equivalence)
{
int maxLabel = *max_element(runLabels.begin(), runLabels.end());
vector<vector<bool>> eqTab(maxLabel, vector<bool>(maxLabel, false));
vector<pair<int, int>>::iterator vecPairIt = equivalence.begin();
while (vecPairIt != equivalence.end())
{
eqTab[vecPairIt->first - 1][vecPairIt->second - 1] = true;
eqTab[vecPairIt->second - 1][vecPairIt->first - 1] = true;
vecPairIt++;
}
vector<int> labelFlag(maxLabel, 0);
vector<vector<int>> equaList;
vector<int> tempList;
cout << maxLabel << endl;
for (int i = 1; i <= maxLabel; i++)
{
if (labelFlag[i - 1])
{
continue;
}
labelFlag[i - 1] = equaList.size() + 1;
tempList.push_back(i);
for (vector<int>::size_type j = 0; j < tempList.size(); j++)
{
for (vector<bool>::size_type k = 0; k != eqTab[tempList[j] - 1].size(); k++)
{
if (eqTab[tempList[j] - 1][k] && !labelFlag[k])
{
tempList.push_back(k + 1);
labelFlag[k] = equaList.size() + 1;
}
}
}
equaList.push_back(tempList);
tempList.clear();
}
cout << equaList.size() << endl;
for (vector<int>::size_type i = 0; i != runLabels.size(); i++)
{
runLabels[i] = labelFlag[runLabels[i] - 1];
}
}
五、基于轮廓的标记
在这里我还是先给出算法描述:
1,从上至下,从左至右依次遍历图像。
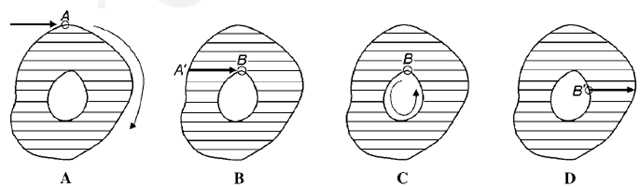
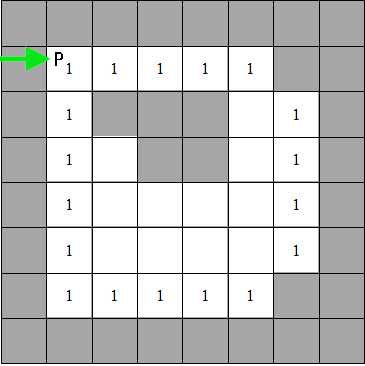
2,如下图A所示,A为遇到一个外轮廓点(其实上遍历过程中第一个遇到的白点即为外轮廓点),且没有被标记过,则给A一个新的标记号。我们从A点出发,按照一定的规则(这个规则后面详细介绍)将A所在的外轮廓点全部跟踪到,然后回到A点,并将路径上的点全部标记为A的标号。
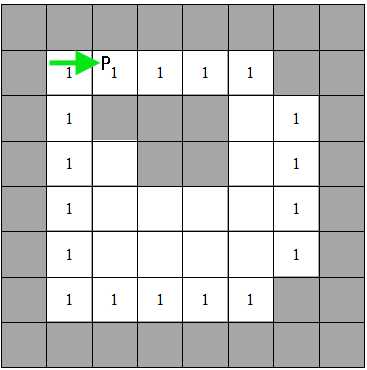
3,如下图B所示,如果遇到已经标记过的外轮廓点A′A′,则从A′A′向右,将它右边的点都标记为A′A′的标号,直到遇到黑色像素为止。
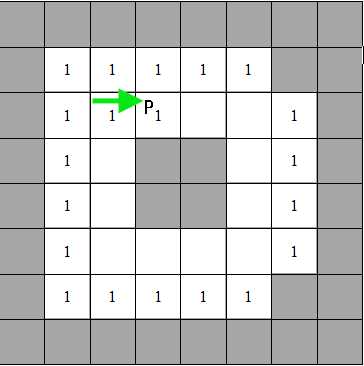
4,如下图C所示,如果遇到了一个已经被标记的点B,且是内轮廓的点(它的正下方像素为黑色像素且不在外轮廓上),则从B点开始,跟踪内轮廓,路径上的点都设置为B的标号,因为B已经被标记过与A相同,所以内轮廓与外轮廓将标记相同的标号。
5,如下图D所示,如果遍历到内轮廓上的点,则也是用轮廓的标号去标记它右侧的点,直到遇到黑色像素为止。
6,结束。
整个算法步骤,我们只扫描了一次图像,同时我们对图像中的像素进行标记,要么赋予一个新的标号,要么用它同行的左边的标号去标记它,下面是算法更详细的描述:
对于一个需要标记的图像II,我们定义一个与它对应的标记图像LL,用来保存标记信息,开始我们把L上的所有值设置为0,同时我们有一个标签变量CC,初始化为1。然后我们开始扫描图像I,遇到白色像素时,设这个点为PP点,我们需要按下面不同情况进行不同的处理:
情况1:如果P(i,j)P(i,j)点是一个白色像素,在LL图像上这个位置没有被标记过,而且PP点的上方为黑色,则P是一个新的外轮廓的点,这时候我们将C的标签值标记给L图像上P点的位置(x,y)(x,y),即L(x,y)=CL(x,y)=C,接着我们沿着P点开始做轮廓跟踪,并把把轮廓上的点对应的L上都标记为C,完成整个轮廓的搜索与标记后,回到了P点。最后不要忘了把C的值加1。这个过程如下面图像S1中所示。
情况2:如果P点的下方的点是unmarked点(什么是unmark点,情况3介绍完就会给出定义),则P点一定是内轮廓上的点,这时候有两种情况,一种是P点在L上已经被标记过了,说明这个点同时也是外轮廓上的点;另一种情况是P点在L上还没有被标记过,那如果是按上面步骤来的,P点左边的点一定被标记了(这一处刚开始理解可能不容易,不妨画一个简单的图,自己试着一个点一个点标记试试,就容易理解了),所以这时候我们采用P点左边点的标记值来标记P,接着从P点开始跟踪内轮廓把内轮廓上的点都标记为P的标号。
下面图像显示了上面分析的两种P的情况,左图的P点既是外轮廓上的点也是内轮廓上的点。
情况3:如果一个点P,不是上面两种情况之一,那么P点的左边一定被标记过(不理解,就手动去标记上面两幅图像),我们只需要用它左边的标号去标记L上的P点。
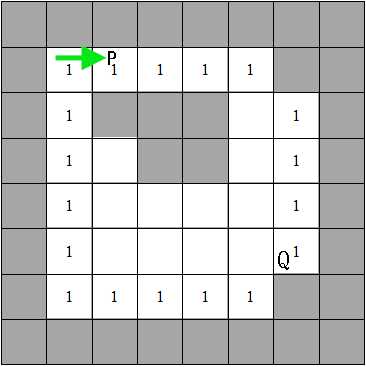
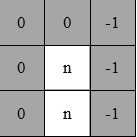
现在我们只剩下一个问题了,就是什么是unmarked点,我们知道内轮廓点开始点P的下方一定是一个黑色像素,是不是黑色像素就是unmarked点呢,显然不是,如下图像的Q点,它的下面也是黑色像素,然而它却不是内轮廓上的点。
实际上在我们在轮廓跟踪时,我们我轮廓点的周围做了标记,在轮廓点周围被查找过的点(查找方式见下面的轮廓跟踪算法)在L上被标记了一个负值(如下面右图所示),所以Q点的下方被标记为了负值,这样Q的下方就不是一个unmarked点,unmarked点,即在L上的标号没有被修改过,即为0。
显然,这个算法的重点在于轮廓的查找与标记,而对于轮廓的查找,就是确定搜索策略的问题,我们下面给内轮廓与外轮廓定义tracker规则。
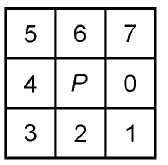
我们对一点像素点周围的8个点分析作一个标号0-7,因为我们在遍历图像中第一个遇到的点肯定是外轮廓点,所以我们先来确定外轮廓的搜索策略,对于外轮廓的点P,有两种情况:
1)如果P是外轮廓的起点,也就是说我们是从P点开始跟踪的,那么我们从7号(右上角)位置P1P1开始,看7号是不是白色点,如果是,则把这个点加入外轮廓点中,并将它标记与P点相同,如果7号点是黑色点,则按顺时针7-0-1-2-3-4-5-6这个顺序搜索直到遇到白点为止,把那个点确定为P1P1,加入外轮廓,并把这个点的标号设置与P点相同。这里很重要一步就是,假设我们2号点才是白点,那么7,0,1这三个位置我们都搜索过,所以我们要把这些点在L上标记为一个负值。如下图所示,其中右图像标记的结果。
2)那么如果P是不是外轮廓的起点,即P是外轮廓路径上的一个点,那么它肯定是由一个点进入的,我们设置为P?1P?1点,P?1P?1点的位置为x(0<=x<=7)x(0<=x<=7),那么P点从(x+2)mod8(x+2)mod8这个位置开始寻找下一步的路径,(x+2)mod8(x+2)mod8是加2取模的意思,它反映在图像就是从P-1点按顺时针数2个格子的位置。确定搜索起点后,按照上面一种情况进行下面的步骤。
外轮廓点的跟踪方式确定了后,内轮廓点的跟踪方式大同小异,只是如果P是内轮廓的第一个点,则它的开始搜索位置不是7号点而是3号点。其他的与外轮廓完全一致。
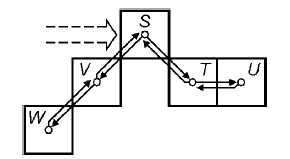
如要上面搜索方式,你不是很直观的理解,不妨尝试着去搜索下面这幅图像,你应该有能有明确的了解了。一个路径搜索结束的条件是,回到原始点S,则S周围不存在unmarked点。
如下边中间图像所示,从S点开始形成的路径是STUTSVWV。
在OpenCV中查找轮廓的函数已经存在了,而且可以得到轮廓之间的层次关系。这个函数按上面的算法实现起来并不困难,所以这里就不再实现这个函数,有兴趣的可以看OpenCV的源码(contours.cpp)。
void bwLabel(const Mat& imgBw, Mat & imgLabeled)
{
// 对图像周围扩充一格
Mat imgClone = Mat(imgBw.rows + 1, imgBw.cols + 1, imgBw.type(), Scalar(0));
imgBw.copyTo(imgClone(Rect(1, 1, imgBw.cols, imgBw.rows)));
imgLabeled.create(imgClone.size(), imgClone.type());
imgLabeled.setTo(Scalar::all(0));
vector<vector<Point>> contours;
vector<Vec4i> hierarchy;
findContours(imgClone, contours, hierarchy, CV_RETR_CCOMP, CV_CHAIN_APPROX_NONE);
vector<int> contoursLabel(contours.size(), 0);
int numlab = 1;
// 标记外围轮廓
for (vector<vector<Point>>::size_type i = 0; i < contours.size(); i++)
{
if (hierarchy[i][3] >= 0) // 有父轮廓
{
continue;
}
for (vector<Point>::size_type k = 0; k != contours[i].size(); k++)
{
imgLabeled.at<uchar>(contours[i][k].y, contours[i][k].x) = numlab;
}
contoursLabel[i] = numlab++;
}
// 标记内轮廓
for (vector<vector<Point>>::size_type i = 0; i < contours.size(); i++)
{
if (hierarchy[i][3] < 0)
{
continue;
}
for (vector<Point>::size_type k = 0; k != contours[i].size(); k++)
{
imgLabeled.at<uchar>(contours[i][k].y, contours[i][k].x) = contoursLabel[hierarchy[i][3]];
}
}
// 非轮廓像素的标记
for (int i = 0; i < imgLabeled.rows; i++)
{
for (int j = 0; j < imgLabeled.cols; j++)
{
if (imgClone.at<uchar>(i, j) != 0 && imgLabeled.at<uchar>(i, j) == 0)
{
imgLabeled.at<uchar>(i, j) = imgLabeled.at<uchar>(i, j - 1);
}
}
}
imgLabeled = imgLabeled(Rect(1, 1, imgBw.cols, imgBw.rows)).clone(); // 将边界裁剪掉1像素
}