某关于数位DP的一节课后的感受

Posted 2021-01-02 u58223-luogu

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了某关于数位DP的一节课后的感受相关的知识，希望对你有一定的参考价值。

题目

求给定区间[x,y]中满足下列条件的整数个数，这个数恰好等于k个互不相等的B的整数次幂之和

Input

15 20 2 2

Out

17 18 20

示例：17=2⁴+2⁰ 18=2⁴+2¹ 20=2⁴+2²

为什么15和16不行呢？？？因为15=2³+2²+2¹+2⁰ 此时K>2明显不成立而16=2³+2³

此时B明显相等就无法通过其实我们可以把它当成B进制的数来算（~~其实我也是听老师讲的~~）

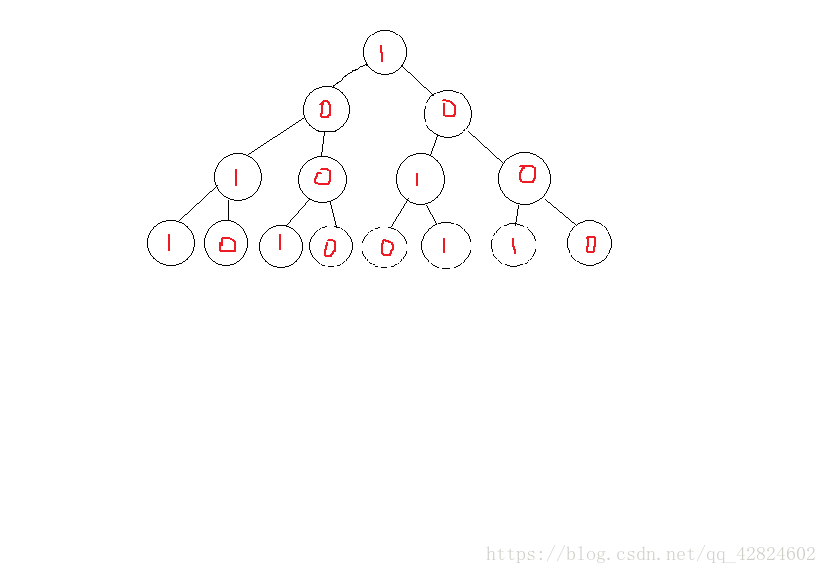
在这里我们把它化成一棵树然后转化成0，1的格式，去寻找它的一的数量是否符合所要求的数

Such As

（好丑，其实是闲着蛋疼画的【图不一定是对的只是为了看得明显一点......】）

这样就可以在树里寻找所满足条件的结果为什么用0和1呢

Because Of

17=2^4+2^0

18=2^4+2^1

20=2^4+2^2

这个实际上就是B进制数

如下：

17=1*2^4+0*2^3+0*2^2+1*2^1+0*2^0

17=10001

同理18=10010 20=10100 15=1111 16=10000

所以说可以在树中找它的1的数量就可以找出答案

//对f进行预处理（变得多多的。。。） 
void init(){
    f[0][0]=1;
    for(int i=1;i<=31;i++){
        f[i][0]=f[i-1][0];
        for(int j=1;j<=i;j++)
            f[i][j]=f[i-1][j]+f[i-1][j-1];//状态转移方程
    }
}

为了给它放进树里所做的努力！！！

然后去搜寻树中的1，一般情况下左子树的1要比右子树的一来得少

当满足条件时就可以记录下来

上面的例子中可以看出有两个1即可

此时就可以存储。。。

int cal(int x,int k){
    int tot,ans;//tot当前路径还有的1的个数 
    for(int i=31;i>0;i--){
        if(x&(1<<i)){
            tot++;
            if(tot>k)break;
            x=x^(1<<i);
        }
        if(1<<(i-1)<=x){
        ans+=f[i-1][k-tot];
        }
    }
    if((tot+x)==k) ans++;
    return x;
}