Dijksrta algorithm

Posted 2021-01-02 dzy521

适用于有向单源最短路径图：

实质：对集合S进行扩大，直至无法扩大，每收集一个点d至集合S，对与该点d直连的点在dist[]中的路径值进行更新。

S = {源点s + 已经确定了最短路径的顶点vi}；

对任一未收录的顶点vi,定义dist[v]为s到v的最短路径长度，但该路径仅经过S中的顶点。

Q1:已确定的最短路为什么必须只经过S中的顶点？

A1:反证法证明。假设存在某个S之外的点tmp使得经过该点到目的点d的路径值最小，那么源点s到点tmp的路径值必小于到点d的路径值，但是我们既然要收录点d，那么比他的路径值小的点必定在这之前收进去了（见Q2）。这与tmp不在S中的条件相悖。

 

Q2:如何确定dist[]中某个值为已确定的最短路径？（如何确定每次往集合S中收录哪个点？）

A2:选dist[]中未收录的路径值最小的。理由如下：设未收录的路径值最小的点为min，假设此时对应的权值不是最短路径，则必存在更短的路径，设该更短的路径经过点tmp，那么在数组dist[]中，tmp对应的路径值应该比min小，与前提条件相悖。(简而言之，就不存在这样的点tmp)

 

Q3:每次为集合S收录一个点，是否会影响其他点的dist[]中的值？

A3:会。增加一个v进入S中，假设影响了另外一个w的dist[]的值，那么v必定在s到w的路径上，并且v和w是直连的。

 

Q4:接Q3，为何v和w是直连的？

A4:假设v和w不直连，则必存在一个中间点tmp，使得v先经过tmp，再经过w。那么根据对dist[]的定义，则tmp必定在S中，但是现在往S中收录的是v，并且v肯定比tmp在dist[]中对应的值小，所以tmp必定不在S中。

所以：每次为集合S收录一个点，影响的是该点直连的点的dist[]值。

dist[w] = min(dist[w],dist[v]+<v,w>权值)

 

算法过程：

(1)初始化S和dist[]，不与源点直连则置为正无穷；

(2)从dist[]中选值最小的收录到S中；

(3)根据Q3，更新dist[]数组；

(4)重复步骤(2)和(3)，直至所有的点已经被收录。

 

伪代码：

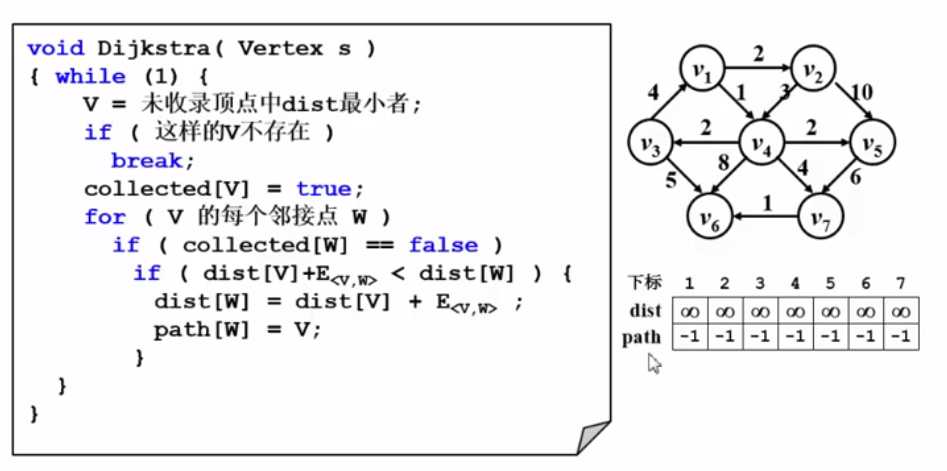
path[]存储最短路径上一个节点

无法处理边的权值为负的情况，因为无法判断dist[V]+E<v,w> < dist[W]是否真正成立。

具体例子网上搜一搜就ok了。