转置卷积的理解

Posted 2021-01-02 wmr95

看了很多反卷积和转置卷积的文章，似乎还是一头雾水，记录下自己理解的过程～

有人一句话总结：逆卷积相对于卷积在神经网络结构的正向和反向传播中做相反的运算。其实还是不是很理解。

反卷积（转置卷积）通常用来两个方面：

1. CNN可视化，通过反卷积将卷积得到的feature map还原到像素空间，来观察feature map对哪些pattern相应最大，即可视化哪些特征是卷积操作提取出来的；

2. FCN全卷积网络中，由于要对图像进行像素级的分割，需要将图像尺寸还原到原来的大小，类似upsampling的操作，所以需要采用反卷积；

3. GAN对抗式生成网络中，由于需要从输入图像到生成图像，自然需要将提取的特征图还原到和原图同样尺寸的大小，即也需要反卷积操作。

我们先来看看卷积和反卷积的图，简直不要太形象。

卷积(convolution):
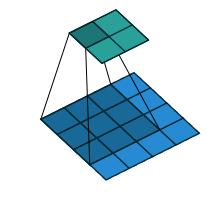
卷积核为 3x3；no padding , strides=1

"反卷积"(the transpose of conv) 可以理解为upsample conv.
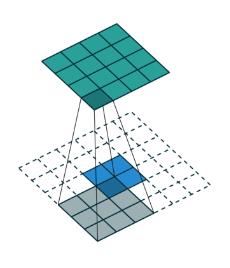
卷积核为:3x3; no padding , strides=1

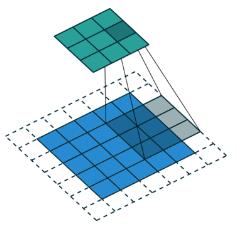
那看下strides=2的时候。
卷积:

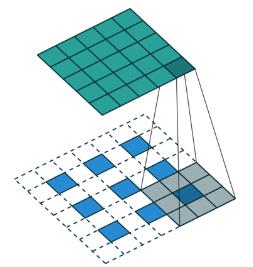
反卷积:

在实际计算过程中，我们要转化为矩阵的乘积的形式，一个转化为Toeplitz matrix一个reshape为列矩阵。
举个简单的例子
比如 input= [3,3],Reshape之后，为A=[1,9]
B(可以理解为滤波器)=[9,4](Toeplitz matrix)
那么A*B=C=[1,4]。Reshape C=[2，2]
所以，通过B 卷积，我们从shape=[3,3]变成了shape=[2,2]

反过来。
输入A=[2,2],reshape之后为[1,4]
B的转置为，[4,9]
那么A*B=C=[1,9],reshape为[3,3]
所以，通过B的转置 - "反卷积"，我们从shape=[2,2]得到了shape=[3,3]

也就是输入feature map A=[3,3]经过了卷积滤波B=[2,2] 输出为 [2,2] ,所以padding=0,stride=1

反卷积则是
输入feature map A=[2,2],经过了反卷积滤波B=[2,2].输出为[3,3].padding=0,stride=1

那么[2,2]的卷积核(滤波器)是怎么转化为[4,9]或者[9,4]的呢？

通过Toeplitz matrix，不清楚自己百度下～

重点来了：对于卷积操作很了解，这里不多说。我们梳理一下反卷积的操作：

首先看stride=1时候的反卷积：这里写的是no padding，但是其实这对应的是正常卷积操作的no padding，然后实际意义上卷积操作是no padding，那么反卷积就是full padding；同时带来一个新的问题，那么padding到底是多少呢？这里我目前理解的是添加的padding值等于（kernel_size - stride），像此处就是padding = kernel_size - stride = 3 - 1 = 2，那么padding添加为2。同样对于下面stride=2的时候，padding = 3 - 2 = 1。（待考证～）

然后，我们来稍微理解一下Toeplitz matrix这个东西，假设我们的输入input = [4,4]，reshape之后是[1,16]，B(可以理解为滤波器)=[16,4](Toeplitz matrix)，那么A*B=C=[1,4]。Reshape C=[2，2]
所以，通过B 卷积，我们从shape=[4,4]变成了shape=[2,2]。

这里，我们的B滤波器为：

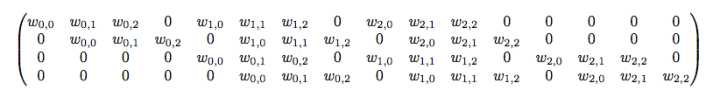
其实这里卷积核B的参数仍然只有9个，加上多个稀疏值0，来构成一个Toeplitz matrix和输入进行矩阵乘积操作。这里为什么B的shape会是16×4呢，因为其实输入是[4,4]，其实是有16个值。