神经网络卷积层与池化层

Posted 2023-03-01 深度不学习。

学习了李沐——《动手学深度学习》的视频课程，在此对知识点进行整理以及记录动手实践中遇到的一些问题和想法。

        首先，我们导入可能用到的包

import torch
from torch import nn

一.卷积层

        关于卷积层的概念，笔者在此不再过多叙述，总之，卷积层的作用是提取输入图片中的信息，这些信息被称为图像特征，这些特征是由图像中的每个像素通过组合或者独立的方式所体现，比如图片的纹理特征，颜色特征。

1.卷积层运算

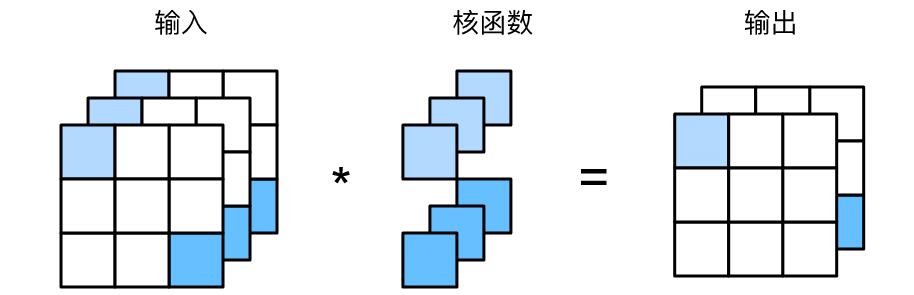
        在神经网络中进行卷积操作可以看作是互相关运算，具体指的是输入张量与核张量之间进行互相关操作产生输出张量。在书中提到的卷积操作的理论描述中，可以总结为卷积核窗口按照设定好的步幅，对输入张量进行按元素做乘法后求和的操作。

        

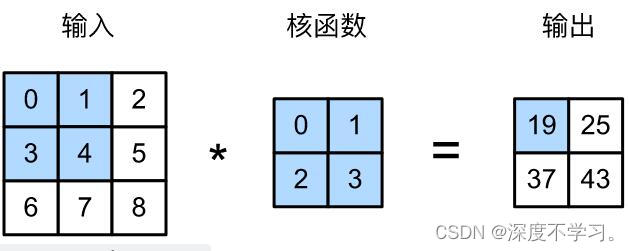
         上图中的操作，可以由下面的数学运算表示：

        

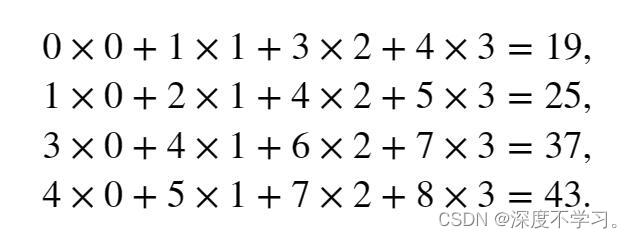
         由于卷积核的宽度和高度都大于1，所以经过卷积操作的输出张量应该是小于（或者等于）输入张量的大小。我们分别将输出张量的高和宽由输入大小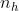X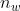，卷积核的高和宽记为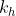X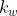记为下式表示：

        

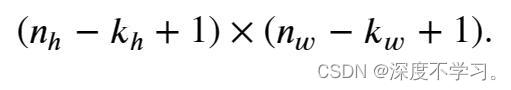
         卷积运算的原理可有以下代码实现：

def corr2d(X, K):  
    """计算二维互相关运算"""
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

        接下来，我们用上述代码验算上图中的卷积运算：

X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
corr2d(X, K)

tensor([[19., 25.],
        [37., 43.]])

2.神经网络卷积层

        卷积层对输入和卷积标量偏置。核权重进行互相关运算，并在添加标量偏置之后产生输出。所以，在卷积层中，我们要训练的参数是卷积核的权重和其标量偏置。

class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

        上述代码中，笔者遇到的问题是nn.Paramater()这个方法。该方法是将一个固定的张量转变成一个可以训练的paramater，并且将这个参数绑定到模型中。笔者试过不用这个方法，直接用torch.full()和torch.zeros()初始化两个参数，最后并不能用state_dict()这个方法得到预设的参数。

3.图像中目标的边缘检测

        书中讲述了一个检测黑白色垂直边缘的方法。在一张通道数为1的图片中，0和1分别表示黑色和白色。

X = torch.ones((6, 8))
X[:, 2:6] = 0
X

tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.]])

        在这个张量中，前两列和最后两列为白色，中间为黑色，我们的目的是要检测出由1变为0以及由0变为1的边界，并分别记为1和-1。

        接下来，我们要构造一个1X2的卷积核，并通过这个卷积核检测出黑白边缘。至于这个卷积核为什么这样来创建，沐导说的是，这个核是通过学习所获得的。

K = torch.tensor([[1.0, -1.0]])

        接下来，我们用最开始创建的方法进行边缘检测。

Y = corr2d(X, K)
Y

tensor([[ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.]])

 4.学习卷积核

        接下来，我们来实现如何学的上述边缘检测中的卷积核。这个过程的主要思想和神经网络的学习类似，在网络中进行训练，得到输出，之后计算模型输出与原数据的损失，再经过梯度下降更新参数，经过若干轮次的迭代，我们便可以求得参数weight（这里我们将偏置忽略掉）。
        

# 构造一个二维卷积层，它具有1个输出通道和形状为（1，2）的卷积核
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)

# 这个二维卷积层使用四维输入和输出格式（批量大小、通道、高度、宽度），
# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2  # 学习率

for i in range(10):
    Y_hat = conv2d(X)
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    # 迭代卷积核
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch i+1, loss l.sum():.3f')

epoch 2, loss 6.567
epoch 4, loss 2.060
epoch 6, loss 0.738
epoch 8, loss 0.285
epoch 10, loss 0.114

        在经过10次的迭代之后，误差便降到足够低，现在我们来看一看我们所学习到的权重张量。

conv2d.weight.data.reshape((1, 2))

tensor([[ 0.9571, -1.0261]])

5.突发奇想

        上文中提到，现有的卷积核只能检测垂直边缘，笔者想将检测垂直边缘的卷积核学习出来。在这里，我们创建一个8X8的张量，将前两行和最后两行标记为白色1，其他位置置0。卷积核的大小设计为2X2。我们最后得到的输出应给是一个7X7的张量。

X = torch.ones((8,8))
X[2:6, :] = 0
Y = torch.zeros(7, 7)
Y[1, :] = 1
Y[-2, :] = -1
print(X)
print(Y)

tensor([[1., 1., 1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1., 1., 1.],
        [0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.],
        [1., 1., 1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1., 1., 1.]])
tensor([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
        [ 1.,  1.,  1.,  1.,  1.,  1.,  1.],
        [ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
        [ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
        [ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
        [-1., -1., -1., -1., -1., -1., -1.],
        [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]])

        具体训练过程如下所示：

c_net = nn.Conv2d(1, 1, kernel_size=2, bias=False)
X = X.reshape((1, 1, 8, 8))
Y = Y.reshape((1, 1, 7, 7))

lr = 0.01
for i in range(10):
    Y_hat = c_net(X)
    l = (Y_hat - Y) ** 2
    c_net.zero_grad()
    l.sum().backward()
    
    c_net.weight.data[:] -= lr * c_net.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch i+1, loss l.sum():.3f')

print(c_net.weight.data)

epoch 2, loss 3.257
epoch 4, loss 0.770
epoch 6, loss 0.204
epoch 8, loss 0.055
epoch 10, loss 0.015
tensor([[[[ 0.8568,  0.1198],
          [-0.2884, -0.6882]]]])

        可以看到，在经过十轮的训练之后，loss已经非常低，而且我们成功学习到了卷积核中的参数weight。我们用这个卷积核中的数据，放到本文最开始我们创建的卷积层中去进行验证。

K = c_net.weight.data.reshape(2,2)
y_hat = corr2d((X.reshape(8, 8), K)
print(y_hat.data)

tensor([[-4.1306e-05, -4.1306e-05, -4.1306e-05, -4.1306e-05, -4.1306e-05,
         -4.1306e-05, -4.1306e-05],
        [ 9.7663e-01,  9.7663e-01,  9.7663e-01,  9.7663e-01,  9.7663e-01,
          9.7663e-01,  9.7663e-01],
        [ 0.0000e+00,  0.0000e+00,  0.0000e+00,  0.0000e+00,  0.0000e+00,
          0.0000e+00,  0.0000e+00],
        [ 0.0000e+00,  0.0000e+00,  0.0000e+00,  0.0000e+00,  0.0000e+00,
          0.0000e+00,  0.0000e+00],
        [ 0.0000e+00,  0.0000e+00,  0.0000e+00,  0.0000e+00,  0.0000e+00,
          0.0000e+00,  0.0000e+00],
        [-9.7667e-01, -9.7667e-01, -9.7667e-01, -9.7667e-01, -9.7667e-01,
         -9.7667e-01, -9.7667e-01],
        [-4.1306e-05, -4.1306e-05, -4.1306e-05, -4.1306e-05, -4.1306e-05,
         -4.1306e-05, -4.1306e-05]])

        可以看到，虽然我们没有真正得到一个只有1、0、-1三个数据组成的张量，但第一行和最后一行的数据太小，我们可以近似看成0，第二行和倒数第二行也可以近似看成1和-1。由此，我们成功学习到了我们所要求的卷积核。

6.填充

        在使用多层卷积时，我们经常丢失边缘像素。由于我们通常使用小卷积核，因此对于任何单个卷积，我们可能只会丢失几个像素。 但随着我们应用许多连续卷积层，累积丢失的像素数就多了。 解决这个问题的简单方法即为填充（padding）：在输入图像的边界填充元素（通常填充元素是0）。

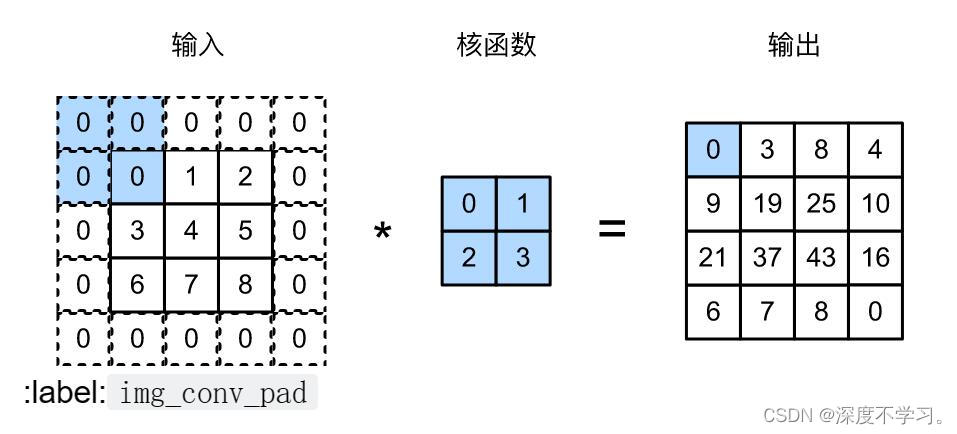
         通常，如果我们添加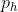行填充（大约一半在顶部，一半在底部）和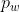列填充（左侧大约一半，右侧一半），则输出形状将为

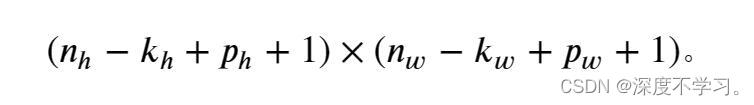
         在许多情况下，我们需要设置和，这样，我们就能让输入张量和输出张量具有相同的高度和宽度，以便我们可以更好的去预测每个图层的输出形状。假设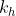是奇数，我们将在高度的两侧填充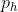行。 如果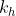是偶数，则一种可能性是在输入顶部填充⌈𝑝ℎ/2⌉行，在底部填充⌊𝑝ℎ/2⌋行。同理，我们填充宽度的两侧。

        我们通常将神经网络中卷积核的高度和宽度设置为奇数，这样我们就可以在保持空间维度的同时，可以在顶部和底部填充相同数量的行，在左侧和右侧填充相同数量的列。

conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)
X = torch.rand(8, 8)
y = conv2d(X.reshape((1, 1)+X.shape))
y.shape[2:]

torch.Size([8, 8])

        总结一下，如果我们想要得到与输入张量相同尺寸的输出张量，那么我们可以将卷积核的高和宽设定为奇数，然后将padding设置成卷积核尺寸减1的一半即可。

7.步幅

        在之前所有的例子中，卷积窗口都是从输入张量的左上角开始，向下、向右滑动，而且每次只滑动一个元素。但是，有时候为了高效计算或是缩减采样次数，卷积窗口可以跳过中间位置，每次滑动多个元素。

        卷积核每次滑动元素的数量称为步幅（stride）。这个超参数的默认数值为1，当我们舍此那个垂直步幅为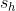，水平步幅为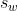时，输出张量的形状就变为

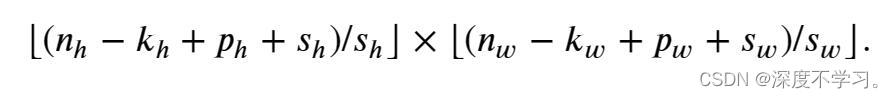
        如果我们设置了 和，输出形状可以简化为

        

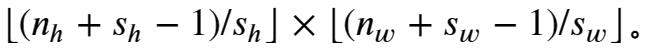
         当输入的高度和宽度都可以被垂直和水平步幅整除时，输出形状就为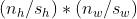。例如下面，我们将将8X8的张量输入进卷积核为3X3，padiing为1，stride为2的卷积层中，就可以得到4X4的输出张量。

conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
y = conv2d(X.reshape(1, 1, 8,8))
y.shape[2:]

torch.Size([4, 4])

8.通道数

        通道数也是卷积层中的一个重要超参数，它分为输入通道数和输出通道数。上文中我们一直用通道数为1的张量做为输入和输出。如果我们将一张彩色图片输入到卷积网络中，此时，输入通道数通常为3（R，G，B）。

(1).多输入通道

        如下所示，我们实现一个计算多输入通道的卷积函数。

def corr2d_multi_in(X, K):
    # 先遍历“X”和“K”的第0个维度（通道维度），再把它们加在一起
    return sum(d2l.corr2d(x, k) for x, k in zip(X, K))

        接下来，我们创建一个通道数为2的输入张量和卷积核。

X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
               [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])

corr2d_multi_in(X, K)

tensor([[ 56.,  72.],
        [104., 120.]])

        最后，我们得到了输出通道为1的输出张量。上述代码我们实现了如下图所示的计算。

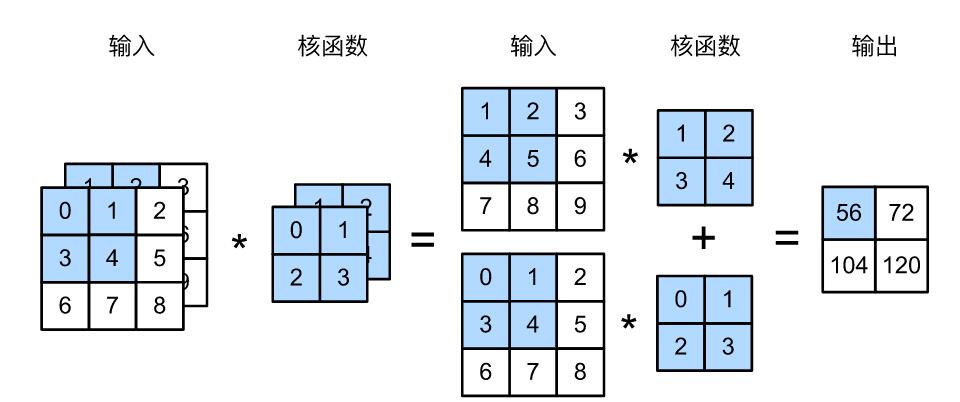
 (2).多输出通道

        同样，我们也可以得到多个通道数的输出。在最流行的神经网络架构中，随着神经网络层数的加深，我们常会增加输出通道的维数，通过减少空间分辨率以获得更大的通道深度。直观地说，我们可以将每个通道看作对不同特征的响应。而现实可能更为复杂一些，因为每个通道不是独立学习的，而是为了共同使用而优化的。因此，多输出通道并不仅是学习多个单通道的检测器。

        在进行多输入通道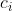，单输出通道的卷积时，我们所设计的卷积核的尺寸为，当我们想得到多输出通道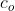的输出张量时，便要设计尺寸为的卷积核。

        下面代码，我们实现一个计算多通道输出的卷积函数。

def corr2d_multi_in_out(X, K):
    # 迭代“K”的第0个维度，每次都对输入“X”执行互相关运算。
    # 最后将所有结果都叠加在一起
    return torch.stack([corr2d_multi_in(X, k) for k in K], 0)

        接下来，我们构造一个具有3个输出通道，并接受2个输入通道的卷积核。

K = torch.stack((K, K + 1, K + 2), 0)
K.shape

torch.Size([3, 2, 2, 2])

        下面，我们让输入张量X，与卷积核K进行互相关计算。

corr2d_multi_in_out(X, K)

tensor([[[ 56.,  72.],
         [104., 120.]],

        [[ 76., 100.],
         [148., 172.]],

        [[ 96., 128.],
         [192., 224.]]])

        可以看到，我们得到了一个3通道的输出张量。

(3).1X1卷积层

        1X1卷积经常包含在复杂深层的网络设计中。因为使用了最小窗口，1×1卷积失去了卷积层的特有能力——在高度和宽度维度上，识别相邻元素间相互作用的能力。 其实1×1卷积的唯一计算发生在通道上。1X1卷积层通常用于调整网络层的通道数量和控制模型复杂性。

        下图展示了1X1卷积核与3个输入通道和2个输出通道的卷积计算。这里输入和输出具有相同的高度和宽度，输出中的每个元素都是从输入图像中同一位置的线性组合。我们可以将1X1卷积层看作是在每个像素位置应用的全连接层，这个全连接层接受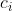个输入，并产生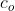个输出。

 二.池化层

        卷积层具有两个目的：降低卷积层对未知的敏感性，同时降低对空间采样表示的敏感性。

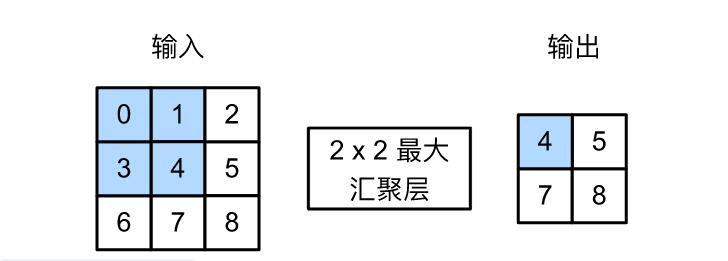
1.最大池化层和平均池化层

        池化层与卷积层十分类似，都有一个固定尺寸的窗口（核），该窗口按照设定的步幅大小在输入张量上滑动。与卷积层不同的是，池化层不会对输入张量进行互相关操作，池化核也不包含参数。池化运算通常是固定的，菲苾是最大池化与平均池化。

        最大池化就是找出被池化窗口所包含的输入张量中，最大的数值。而平均池化是计算被池化窗口所包含的输入张量所有数值的平均数。

def pool2d(X, pool_size, mode='max'):
    p_h, p_w = pool_size
    Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
    return Y

        我们构建图片中的输入张量，并创建2X2的池化核。

X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
pool2d(X, (2, 2))

tensor([[4., 5.],
        [7., 8.]])

        此外，我们还可以验证以下平均池化层。

pool2d(X, (2, 2), 'avg')

tensor([[2., 3.],
        [5., 6.]])

2.填充和步幅

        与卷积层类似，池化层也有填充padding以及步幅stride。默认情况下，深度学习框架中池化层的步幅大小与池化窗口的大小相同。

X = torch.arange(16, dtype=torch.float32).reshape((1, 1, 4, 4))
pool2d = nn.MaxPool2d(3)
pool2d(X)

tensor([[[[10.]]]])

        同样，填充和步幅都可以手动设定。

        

pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)

tensor([[[[ 5.,  7.],
          [13., 15.]]]])

3.多个通道

        在处理多个通道时，池化层在每个输入通道上进行单独运算，而不是像卷积层一样在通道上对输入进行汇总。这就意味着，在池化层中，输出通道数与输入通道数是相同的。

X = torch.cat((X, X + 1), 1)
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)

tensor([[[[ 5.,  7.],
          [13., 15.]],

         [[ 6.,  8.],
          [14., 16.]]]])

三.总结实验

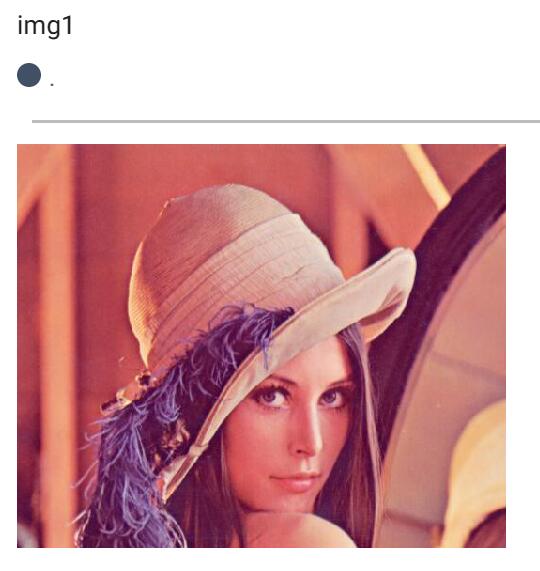
        接下来，笔者写了一段代码，将一张3通道的输入图片，转化成了1通道的图片。在此代码中，运用了卷积层和池化层。

from torch import nn
from PIL import Image
from torch.utils.tensorboard import SummaryWriter
from torchvision.transforms import transforms

writer = SummaryWriter('./log_demo')

img_path = 'demo.jpg'
img = Image.open(img_path)

trans = transforms.ToTensor()
img_tensor = trans(img)

net = nn.Sequential(
    nn.Conv2d(in_channels=3, out_channels=1, kernel_size=3, padding=1),
    nn.MaxPool2d(3, stride=1)
)

img_out = net(img_tensor)

writer.add_image('img1', img_tensor.reshape(3, 430, 521))
writer.add_images('img2', img_out.reshape(-1, 1, 428, 519))

writer.close()

        我们来看一下效果。

输入

输出