B-树 动机与结构

Posted 2021-01-01 hongshijie

Ps.我们遵循从感性到理性的认知顺序来逐步探索B-树的奥秘，之前经常说的value这里用key（关键码）指代，因为可能存的是字符串，说是value就不合适了。

（多图预警！！！建议在WI-FI下观看） 

虽然迄今为止我们所看到的查找树皆为二叉树，但还有另一种常用的查找树与此相异，名为B- 树，又叫B树。下面是B-树的基本信息

在物理上，B-树的每一个节点都可能包含多个分支，然而后面会看到，从逻辑上讲，它依然等效于此前所介绍的二叉查找树，因此我们依然把它归入搜索树的范畴。那已经有了之前那么多的种类，设计和实现B-树的动机何在呢？B树最初也是最主要的功能，在于弥合不同存储级别之间在访问速度上的巨大差异——也就是实现高效的IO。先让我们穿越到37年前，那时Bill Gates的一句话曾经被很多人当作笑柄。

因为他在那时曾经断言640KB也就是dos的基本内存容量，已经足以满足任何实际应用的需要了。虽然这话有点武断，但在学习完B树以后，我们一定会认为这句话实际上是千真万确的真理，因为我们有各种各样的玄学优化手段2333。

 

从某种意义上讲，我们在计算过程中能够使用的内存是在日益的变小，而不是如我们直觉一样，变得越来越大。这听起来似乎是个悖论，但原因在于需要处理的信息量级越来越大：系统存储容量的增长速度<<应用问题规模的增长速度。不妨来看这样一组统计数字

而我们人类所拥有的数字化信息的总量，在过去的半个多世纪中增长速度是惊人的，比如截至2010年总量以及达到Zettabyte——1后面要接21个0。我们知道中国的人口大致是十多亿，也就是$10^{9}$左右，分摊下去每个人都需要一个TB规模的硬盘（如果硬盘里女朋友比较多这空间还不够呢233），注意，这里我们说的还只是硬盘，是外部存储。而如果考虑内存，那这方面的压力就更大了。

不妨来进一步看一些数字，对不同年代典型的数据库规模和内存规模做个对比：

 

短短20年，内存规模跃升1000倍，但是数据规模则跃升了百万、千万倍。内存容量的压力其实更大了，这个压力提高了至少100倍。而如今典型的数据集已经大多以TB作为度量单位了，无论是生物分子学、医学、物理学，还是核能、气象等领域。随便举几个例子

 

总而言之，尽管随着技术的发展，内存的绝对容量的确是在增加，但是相对于实际应用的需求而言，内存的容量实际上是在越来越小。那为什么不把内存做大一点啊？原因在于，经费你给拨么？我们必须在容量与访问速度之间做取舍，组成原理里讲过，存储器的容量越大速度就越慢，反过来，为了使得访问速度更快，就不得不在容量上做必要的牺牲。面对这个内在矛盾，我们还是可以有所作为的，运用矛盾分析法，我们想到了一种绝妙的方法——Cache！为此我们需要对不同层次存储器的性能做进一步的了解：

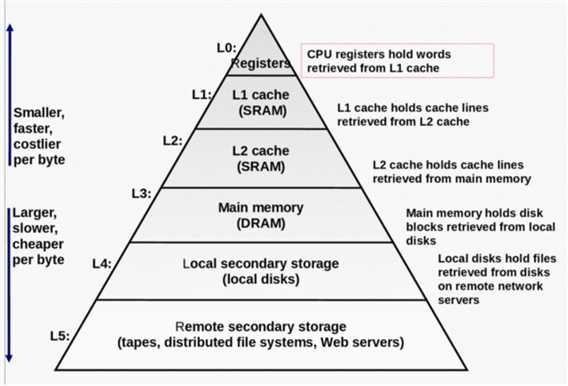
这包括两个事实

1. 容量和类型不同的存储器，在访问速度上的差异是极其悬殊的

就以磁盘、内存这两级存储为例，他们在访问速度上的差异究竟有多大呢？就传统的旋转式磁盘而言，访问速度大致是ms级。而典型的内存呢，大致是在ns级，不要小看了m和n之间的差异,以一秒为基准——前者是$10^{-3}$，而后者是$10^{-9}$。故二者的差异大致是在$10^{5}$至$10^{6}$。即使保守的估计也是5个数量级。就是一秒之于一天的差距。如果将内存的一次访问比作是1s，那么响应的一次外存操作则是1 day。这个差距很令人绝望了……《醒世恒言》里形象的说过：山中方七日，世上已千年。

因此在设计与实现算法的时候，为了避免一次外存访问，我们宁可访问内存十次、百次甚至千次、万次也在所不惜。这也是为什么通常存储系统都是按层次分级组织的。随着层次的深入，存储器的容量越来越大，但是反过来，访问的速度也越来越低。这样一种分级的结构之所以能够高效的运转，在于其中采用的一种策略：将最常用的数据尽可能放在更高的层次，因为尽管它的存储容量有限但速度最高，而不常用的数据会自适应的转移到更大，但是速度更慢的级别中去。

 

2. 从磁盘读写1B，与读写1KB几乎一样快

典型的存储系统的确大多是采用批量式的方式来支持读或者写操作的。具体来说，无论我们是需要从内存向外存输出数据，还是需要从外存向内存读入数据，涉及的数据都是以页面为单位进行核算和组织的。比如在C的stdio.h中有这样一段代码：

其中setvbuf接口就允许设置页面缓冲区的大小，缓冲的工作模式等。因此在涉及频繁而大量数据访问的算法中，就要充分利用这个特性，也就是说我们要逐渐习惯批量式的访问。要么一次性大量读写，要么就什么也不做。就边际成本而言，这样的组织和访问方式才能够达到尽可能的优化。那么我们的主角B-树在其间又能起到一个什么样的作用呢？

那我们来探究一下B-树的内部了。 

B树也是用来存放一组具有关键码的词条的，它的特点也非常的鲜明，首先每一个节点未必只有两个分叉，可以拥有更多的分叉。其次，所有底层节点的深度都是完全一致的，从这个意义上讲它是一种理想平衡的搜索树。最后，也是最重要的一个整体特征：相对于常规的二叉查找树，B树会显得更宽、更矮，而且也是可以动态变化的。B树的设计者将其定义为一种平衡的多路（multi-way）搜索树，与之前的二路搜索树在本质上是等价的，因为每一个内部（internal）节点都可以认为是由若干个二路节点经过适当的合并以后得到的

 

举个例子，看这个

 

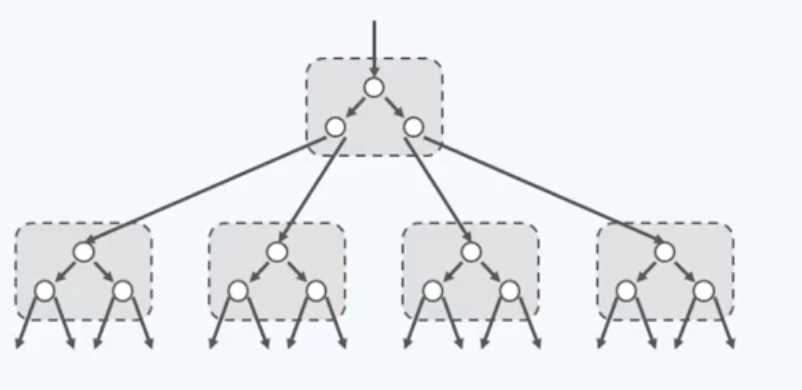
不看方框，这就是一颗BST，看了方框，把父子两代合并为一个节点，这棵树就变成了这样：

 

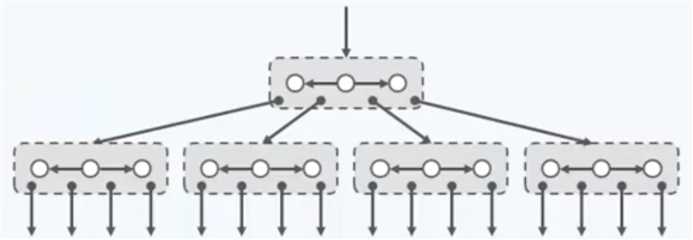
2代合并后，每个节点都将拥有3个关键码，以及4个分支。推而广之，3代合并后，每个节点里含有7个关键码以及8路分支。一般而言， 如果每d代都进行一次合并，那么之后的每个节点都将拥有$2^{d}$路分支，以及相应再减少1个单位的关键码。那既然这种多路的搜索树与二路搜索树并没有本质的区别，那还发明个鬼啊，难道这是灌水论文？

 

非也非也，问题在于我们通常都是按多个层次来分级组织的存储系统，如果使用B树可以针对不同层次间的通信，大大降低IO访问的次数，从而极大的提高计算效率。那难道之前很熟悉的AVL树在这方面还不够么？

 

我们来做个小学算术，有一个由$10^{9}$，1G个记录的数据集。如果将它们组织为一棵AVL树，高度大致为30层。也就是说在最坏的情况下，单次查找需要深入30层，而每一层我们都需要执行一次IO操作，而每一次只能读一个值，这就很得不偿失了。那B树呢，B树中合并后节点同时包含多个而不是单个关键码，因此在B树中每下降一层，都能以内部节点为单位读入一组而不是单个关键码，从而将外存批量访问的特点转化为实在的优点。一个内部节点的规模取决于数据缓冲页面的大小，通常的情况下都是几个KB。比如若将内部节点的规模取做256，$2^{8}$。那同样存1G个记录的B树高度不会超过4，这就意味着即便在最坏的情况下，单次查找所需的IO也同样不超过4次，这是一个很大的提高了。或许有些人会有疑问：这不都是常数级别么？就渐近意义而言是这样，但是当这个常数的每一个单位都相当于10⁵至10⁶时，就必须计较一下了，因为我们的内存和时间都是有限的。就像1秒和1天都可以视作是常数，但是对于有限的人生来说，却有本质的区别，4年读一个学士大家能接受，如果换成30年，就没人这么干了。

 

有了以上的感性认识，我们从理性上洞察一下B-树为何物。每一颗B-树都有自己的阶次，这是它的固有属性。M阶B-树是一颗具有以下结构特征的树：

1. 树根处限制：0个儿子 or 儿子数量在2和M之间
2. 除树根外，所有非叶节点的儿子数量在$leftlceil frac{M}{2} ight ceil$和M之间
3. 所有的树叶都在相同深度，外部节点也在相同深度
4. 每个内部节点有不超过M-1个关键码

 

换句话讲，M这个指标规定了B-树内部节点和分支的上下界：M阶B树每个节点最多有M条分支，除根之外，其他节点至少有$leftlceil frac{M}{2} ight ceil$条分支，这棵树又叫（$leftlceil frac{M}{2} ight ceil$，M）-树。节点最多存M-1个值，其他的节点至少有实际分支数-1个值（by wikipedia）。对于4阶B树而言，也可以称之为(2,4)树，有趣的是，(2,4)树在B树中具有非常独特的作用和地位，后面我们将会看到(2,4)树与红黑树有不解的渊源。这篇写B-树分析，下篇写具体实现，再下一篇就写红黑树。

 

 

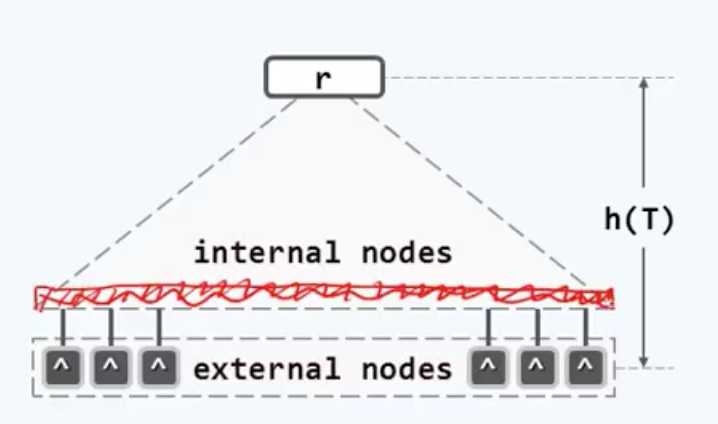
红色的部分是真实存在的叶子结点，在很多文献中可以和“外部节点”互称，但在B-树中这是两个完全不同的概念。另外B-树的高度是把外部节点也计入在内的，与通常的BST不同。还需要说明的是，关于B-树的表示问题，因为他特殊的性质导致很多情况下要预留出很多指针位，具体来说就是，如果需要完整的将一棵B树画出来，那就要为每一个关键码的左右后代画出2个指针，如下

 

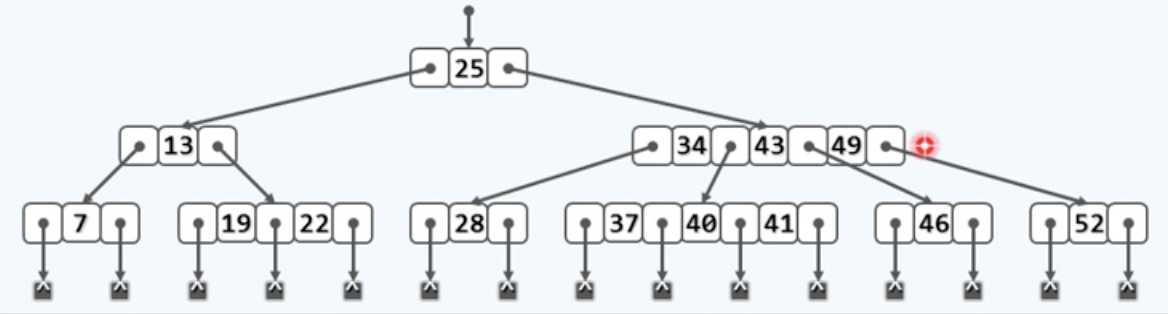
但是纸没那么大，所以要紧凑一点来表示，我们把这些指针简化为质点，变成这样： 

 

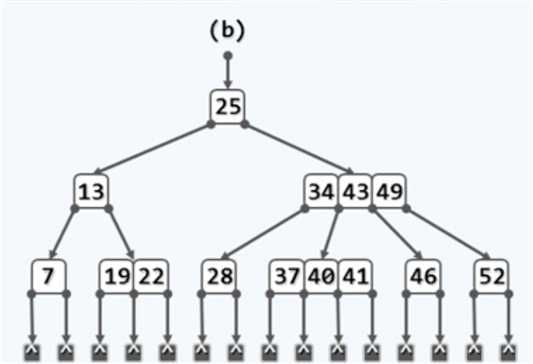
而外部节点都在同一层，没有差异，就把它忽略掉，我们只关注不同点。可以这样表示：

 

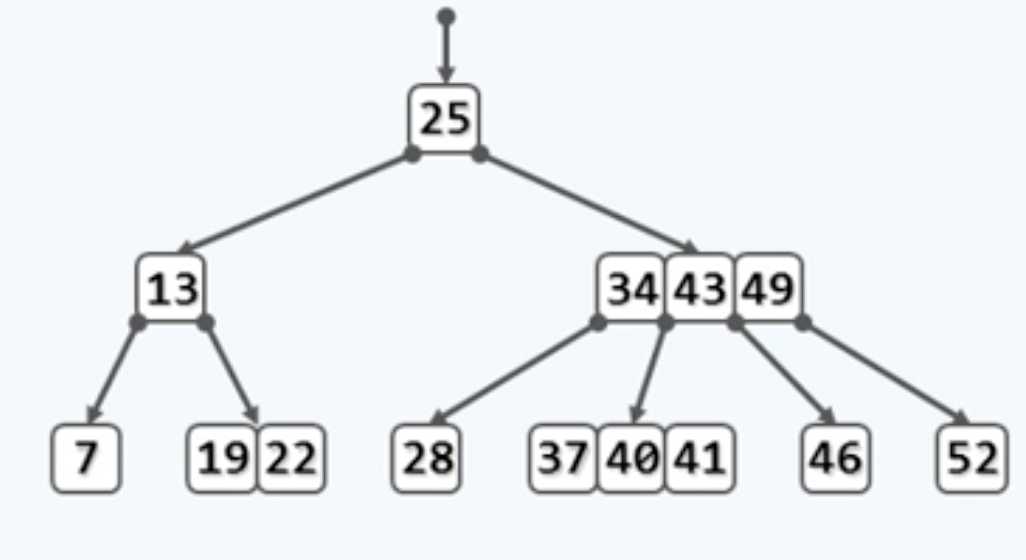
或者这样：

 

 

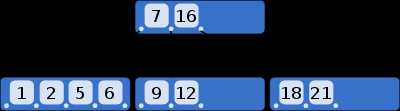
 如此一来就能节省篇幅地表达巨量的数据和引用了。但是画归画，实际上心里还是要明白，里面存在大量的外部节点和引用。接下来的一个问题自然就是：“你说的道理我懂,可是为什么鸽子那么大？” 该如何实现B-树呢？又该如何完成配套的一系列维护操作呢？各位下篇见，明天6点左右发。