排序之损失函数(系列2)
Posted AI蜗牛之家
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了排序之损失函数(系列2)相关的知识,希望对你有一定的参考价值。
文章目录
- 1.Ranking Loss 函数:度量学习
- 2.Ranking Losses 表述
- 3.Ranking Loss 的其他命名
- 4.Siamese 和 triplet 网络
- 5.使用 Ranking Loss 做多模态检索
- 6.深度学习框架中的 Ranking Loss 层
- 参考链接
继上一篇排序之指标集锦(系列1)排序指标介绍之后,继续梳理排序中的损失函数。
Ranking Loss被用于很多领域和神经网络任务中(如 Siamese Nets 或 Triplet Nets),这也是它为什么拥有 Contrastive Loss、Margin Loss、Hinge Loss 或 Triplet Loss 等这么多名字的原因。
1.Ranking Loss 函数:度量学习
像 Cross-Entropy Loss 或 Mean Squear Error Loss 这些 Loss 函数,它们的目的是为了直接预测一个标签或一个值,而 Ranking Loss 的目的是为了预测输入样本间的相对距离。这样的任务通常被称作度量学习。
Ranking Loss 函数在训练数据方面非常灵活:我们只需要知道数据间的相似度分数,就可以使用它们。这个相似度分数可以是二维的(相似/不相似)。例如,想象一个面部识别数据集,我们知道哪些人脸图像属于同一个人(相似),哪些不属于(不相似)。使用 Ranking Loss 函数,我们可以训练一个 CNN 网络,来推断两张面部图像是否属于同一个人。
要使用 Ranking Loss 函数,我们首先要定义特征抽取器,它能从 2 个或 3 个样本中抽取表征样本的 embedding;接着我们定义一个能度量他们相似度的函数,如欧拉距离;最后,我们训练特征抽取器,在相似样本的条件下,所产生出的 embeddings 的距离相近,反之对于不相似的样本,它们的距离较远。
我们不关心表征 embedding 所对应的值,只关心它们的距离。然而,这种训练方法已经证明可以为不同的任务产生强大的表征。
2.Ranking Losses 表述
Ranking Losses 有不同的名称,但在大多数场景下,它们的表述是简单的和不变的。我们用于区分不同 Ranking Loss 的方式有 2 种:二元组训练数据(Pairwise Ranking Loss)或三元组训练数据(Triplet Ranking Loss)。
这两者都会比较训练数据的表征之间的距离。
2.1.Pairwise Ranking Loss
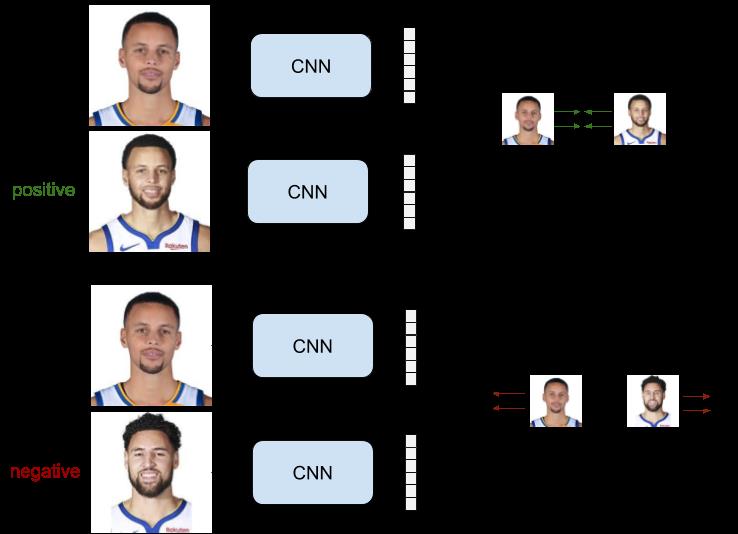
该设置会用到正样本对和负样本对训练集,正样本对包含锚样本
x
a
x_a
xa和正样本
x
p
x_p
xp,
x
p
x_p
xp和
x
a
x_a
xa相似,负样本对由锚样本
x
a
x_a
xa和负样本
x
n
x_n
xn 组成,在度量中它和
x
a
x_a
xa不相似。
对于正样本对,目标是学习它们的表达,使它们之间的距离
d
d
d 越小越好;而对于负样本对,要求样本之间的距离超过一个边距
m
m
m。 Pairwise Ranking Loss 要求正样本对之间的表达的距离为 0,同时负样本对的距离要超过一个边距(margin)。我们用
r
a
r_a
ra,
r
p
r_p
rp 和
r
n
r_n
rn 来分别表示锚样本、正样本和负样本的表达,
d
d
d 是一个距离函数,则可以写成:
L
=
d
(
r
a
,
r
p
)
i
f
P
o
s
i
t
i
v
e
P
a
i
r
m
a
x
(
0
,
m
−
d
(
r
a
,
r
n
)
)
i
f
N
e
g
a
t
i
v
e
P
a
i
r
L = \\left\\\\beginmatrix & d(r_a,r_p) & & if & PositivePair \\\\ & max(0, m - d(r_a,r_n)) & & if & NegativePair \\endmatrix\\right.
L=d(ra,rp)max(0,m−d(ra,rn))ififPositivePairNegativePair
对于正样本对,只有当网络产生的两个元素的表征没有距离时,损失才是0,损失会随着距离的增加而增加。
对于负样本对,当两个元素的表征的距离超过边距 m m m时,损失才是0。然而当距离小于 m m m时,loss 为正值,此时网络参数会被更新,以调整这些元素的表达,当 r a r_a ra和 r n r_n rn的距离为 0 时,loss 达到最大值 m m m。边距的作用是,当负样本对产生的表征距离足够远时,就不会把精力浪费在扩大这个距离上,所以进一步训练可以集中在更难的样本上。
假设
r
0
r_0
r0和
r
1
r_1
r1是样本的表征,
y
y
y为 0 时表示负样本对,为 1 时表示正样本对,距离用欧拉距离来表示,我们还可以把 Loss 写成:
L
(
r
a
,
r
p
,
r
n
)
=
y
d
(
r
a
,
r
p
)
+
(
1
−
y
)
m
a
x
(
0
,
m
−
d
(
r
a
,
r
n
)
)
L(r_a,r_p,r_n) = y d(r_a,r_p) + (1-y)max(0, m-d(r_a,r_n))
L(ra,rp,rn)=yd(ra,rp)+(1−y)max(0,m−d(ra,rn))
2.2.Triplet Ranking Loss
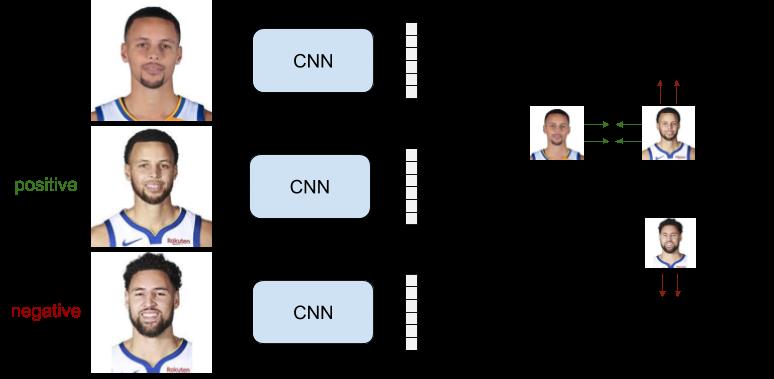
使用 triplet 三元组的而不是二元组来训练,模型的表现更好。Triplets 三元组由锚样本 x a x_a xa,正样本 x p x_p xp,和负样本 x n x_n xn 组成。 模型的目标是锚样本和负样本表达的距离 d ( r a , r n ) d(r_a, r_n) d(ra,rn)要比锚样本和正样本表达的距离 d ( r a , r p ) d(r_a, r_p) d(ra,rp)大一个边距 m m m。 我们可以这样写: L ( r a , r p , r n ) = m a x ( 0 , m + d ( r a , r p ) − d ( r a , r n ) ) L(r_a,r_p,r_n) = max(0,m + d(r_a,r_p) - d(r_a,r_n)) L(ra,rp,rn)=max(0,m+d(ra,rp)−d(ra,rn))
一起来分析下该 loss 的 3 种情况:
Easy Triplets:
d
(
r
a
,
r
n
)
>
d
(
r
a
,
r
p
)
+
m
d(r_a,r_n) > d(r_a,r_p) + m
d(ra,rn)>d(ra,rp)+m,相对于正样本和锚样本之间的距离,负样本和锚样本的距离已经足够大了,此时 loss 为 0,网络参数无需更新。
Hard Triplets:
d
(
r
a
,
r
n
)
<
d
(
r
a
,
r
p
)
d(r_a,r_n) < d(r_a,r_p)
d(ra,rn)<d(ra,以上是关于排序之损失函数(系列2)的主要内容,如果未能解决你的问题,请参考以下文章