第九届福建省大学生程序设计竞赛 2018.8.26组队训练赛
Posted dillonh
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了第九届福建省大学生程序设计竞赛 2018.8.26组队训练赛相关的知识，希望对你有一定的参考价值。
题目链接：http://acm.fzu.edu.cn/contest/list.php?cid=158
A题题目：
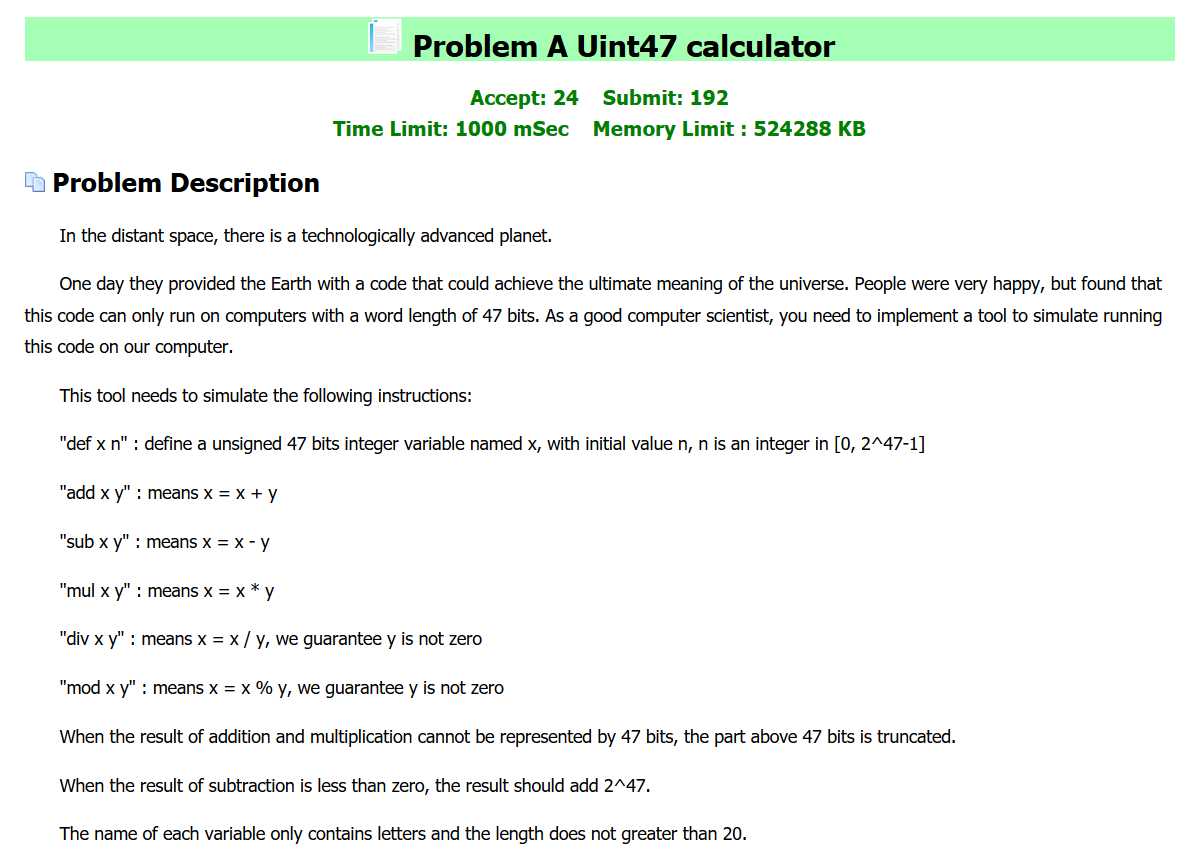
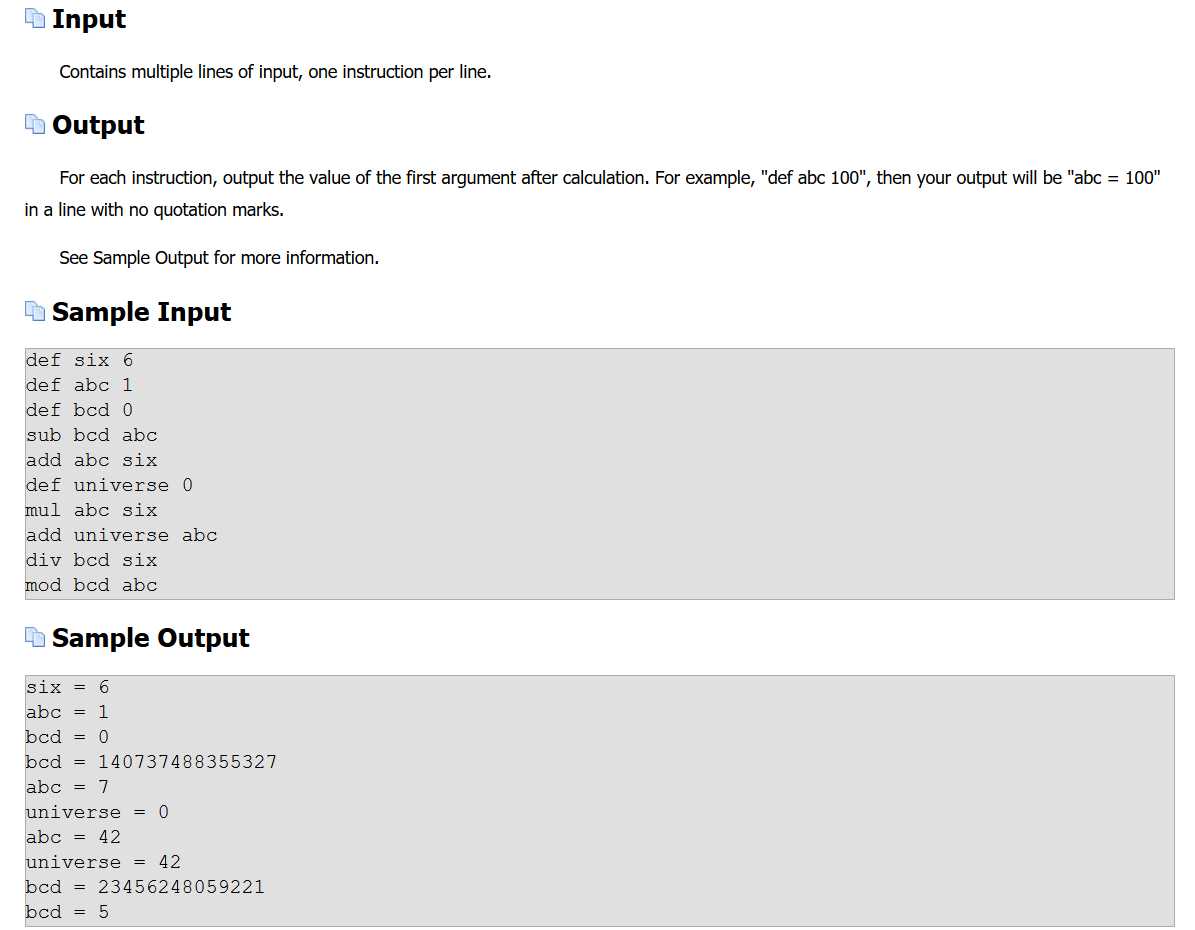
题意：
给你六种操作：def， mul，mod，div， add， sub。除了看这几个字母也都知道是啥意思了，其中def是进行define。
思路：
比赛时队友写的，直接模拟，不过赛后补题时队友和我说mul时需要快速乘。
代码实现如下：
1 #include <set> 2 #include <map> 3 #include <queue> 4 #include <stack> 5 #include <cmath> 6 #include <bitset> 7 #include <cstdio> 8 #include <string> 9 #include <vector> 10 #include <cstdlib> 11 #include <cstring> 12 #include <iostream> 13 #include <algorithm> 14 using namespace std; 15 16 typedef long long LL; 17 typedef pair<LL, LL> pLL; 18 typedef pair<LL, int> pli; 19 typedef pair<int, LL> pil;; 20 typedef pair<int, int> pii; 21 typedef unsigned long long uLL; 22 23 #define lson i<<1 24 #define rson i<<1|1 25 #define lowbit(x) x&(-x) 26 #define bug printf("********* "); 27 #define debug(x) cout<<"["<<x<<"]" <<endl; 28 #define FIN freopen("D://code//in.txt", "r", stdin); 29 #define IO ios::sync_with_stdio(false),cin.tie(0); 30 31 const double eps = 1e-8; 32 const LL mod = 1LL<<47; 33 const int maxn = 1e6 + 7; 34 const double pi = acos(-1); 35 const int inf = 0x3f3f3f3f; 36 37 LL x; 38 string op, s, t; 39 map<string, LL> mp; 40 41 LL mul(LL a, LL b) { 42 LL ans = 0; 43 while(b) { 44 if(b & 1) ans = (ans + a) % mod; 45 a = a * 2 % mod; 46 b >>= 1; 47 } 48 return ans % mod; 49 } 50 51 int main() { 52 //FIN; 53 IO; 54 while(cin >>op) { 55 if(op == "def") { 56 cin >>s >>x; 57 mp[s] = x % mod; 58 cout <<s <<" = " <<mp[s] <<endl; 59 } else if(op == "sub") { 60 cin >>s >>t; 61 mp[s] = (mp[s] - mp[t] + mod) % mod; 62 cout <<s <<" = " <<mp[s] <<endl; 63 } else if(op == "add") { 64 cin >>s >>t; 65 mp[s] = (mp[s] + mp[t]) % mod; 66 cout <<s <<" = " <<mp[s] <<endl; 67 } else if(op == "div") { 68 cin >>s >>t; 69 mp[s] = (mp[s] / mp[t] + mod) % mod; 70 cout <<s <<" = " <<mp[s] <<endl; 71 } else if(op == "mul") { 72 cin >>s >>t; 73 mp[s] = mul(mp[s], mp[t]) % mod; 74 cout <<s <<" = " <<mp[s] <<endl; 75 } else { 76 cin >>s >>t; 77 mp[s] = mp[s] % mp[t]; 78 cout <<s <<" = " <<mp[s] <<endl; 79 } 80 } 81 return 0; 82 }
B题最大权闭合子图，待补。
D题题目：
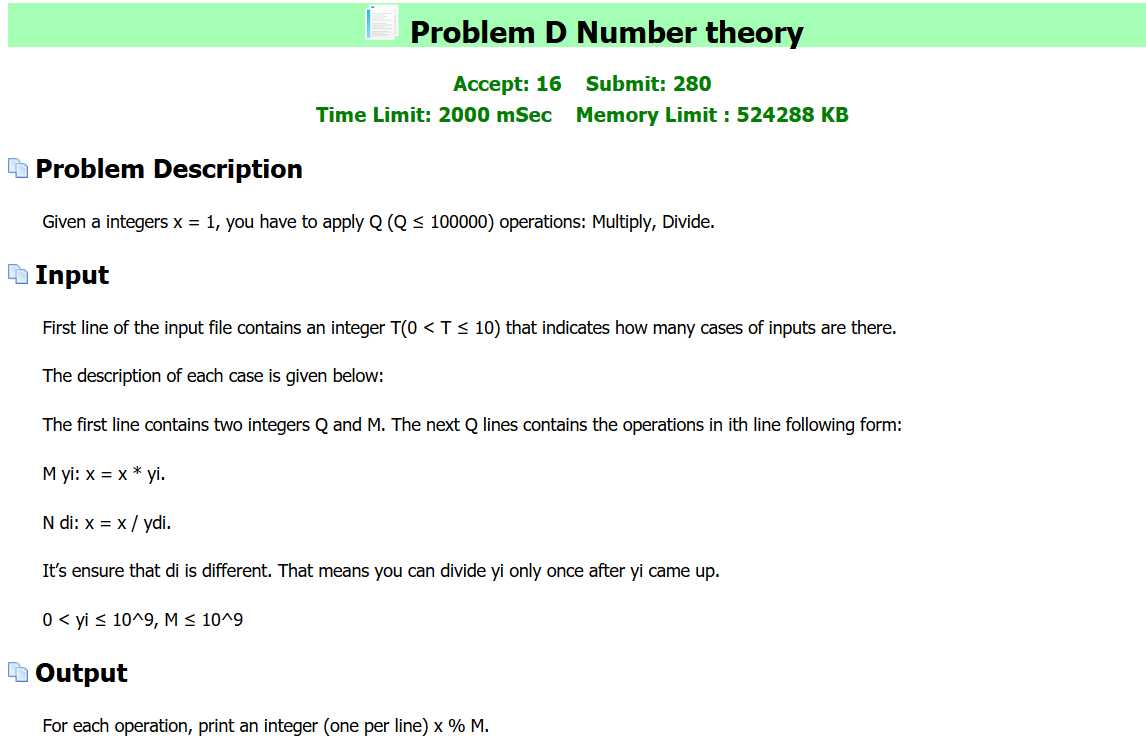
题意：
对于一个x，初始值为1，进行q次操作，模数是m。操作种类有两种：乘以x，处以第x次操作的那个数，每次操作输出x。
思路：
比赛时队友耿直的进行模拟，自信WA了。然后帮他debug没搞出来就换我来写，我一上来就来了JAVA大数和C++大数，都T了。正在无解时，突然发现每个除的数只会被除一次，然后想到一个骚操作，没想到是正解~对于乘法很容易，对于除法：我们除了那个数就相当于前面没有乘以那个数，那么我们该如何记录没有进行第x次操作其他操作全都进行了呢？我和队友说这个思路时，突然想到线段树，我们以操作的步数为区间，如第一次操作就是大区间的左端点，q为右端点。每次乘就是将当前对应的那个点的值update为x，除就是将第x次操作对应的那个值update为1，输出的结果则是从1到当前操作的值的乘积。具体情况看代码~
代码实现如下：
1 #include <set> 2 #include <map> 3 #include <queue> 4 #include <stack> 5 #include <cmath> 6 #include <bitset> 7 #include <cstdio> 8 #include <string> 9 #include <vector> 10 #include <cstdlib> 11 #include <cstring> 12 #include <iostream> 13 #include <algorithm> 14 using namespace std; 15 16 typedef long long LL; 17 typedef pair<LL, LL> pLL; 18 typedef pair<LL, int> pli; 19 typedef pair<int, LL> pil;; 20 typedef pair<int, int> pii; 21 typedef unsigned long long uLL; 22 23 #define lson rt<<1 24 #define rson rt<<1|1 25 #define IO ios::sync_with_stdio(false),cin.tie(0); 26 27 const double eps = 1e-8; 28 const int mod = 1e9 + 7; 29 const int maxn = 1e5 + 7; 30 const double pi = acos(-1); 31 32 int t, q, m, x; 33 char s[5]; 34 35 struct node { 36 int l, r; 37 LL mul; 38 }segtree[maxn<<2]; 39 40 void push_up(int rt) { 41 segtree[rt].mul = ((segtree[lson].mul % m) * (segtree[rson].mul % m)) % m; 42 } 43 44 void build(int rt, int l, int r) { 45 segtree[rt].l = l, segtree[rt].r = r; 46 segtree[rt].mul = 1; 47 if(l == r) return; 48 int mid = (l + r) >> 1; 49 build(lson, l, mid); 50 build(rson, mid + 1, r); 51 push_up(rt); 52 } 53 54 void update(int rt, int pos, int val) { 55 if(segtree[rt].l == pos && segtree[rt].r == pos) { 56 segtree[rt].mul = val; 57 return; 58 } 59 int mid = (segtree[rt].l + segtree[rt].r) >> 1; 60 if(pos <= mid) update(lson, pos, val); 61 else update(rson, pos, val); 62 push_up(rt); 63 } 64 65 int main() { 66 scanf("%d", &t); 67 while(t--) { 68 scanf("%d%d", &q, &m); 69 build(1, 1, q); 70 for(int i = 1; i <= q; i++) { 71 scanf("%s%d", s, &x); 72 if(s[0] == ‘M‘) { 73 update(1, i, x); 74 } else { 75 update(1, x, 1); 76 } 77 printf("%lld ", segtree[1].mul); 78 } 79 } 80 return 0; 81 }
E题题目：
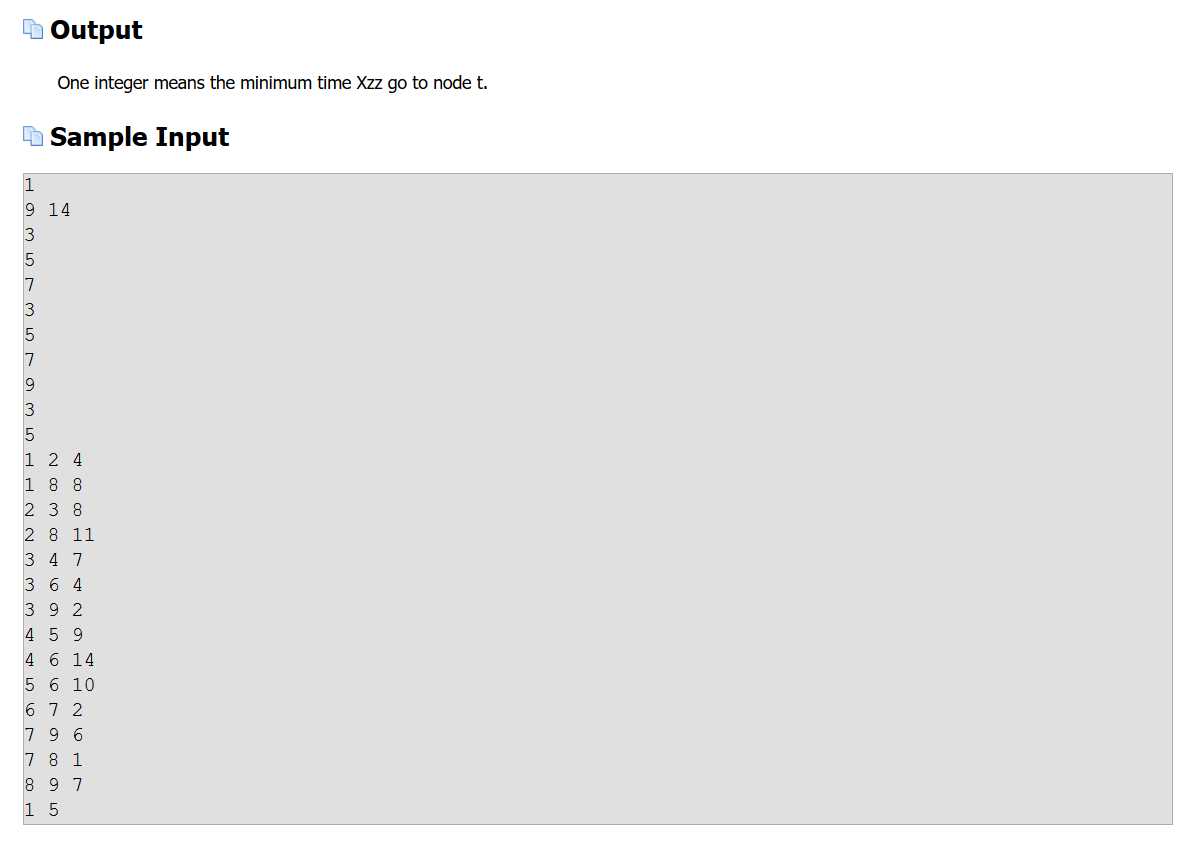
题意：
一个n个节点m条边的无向图，要求出s到t的最短时间。每条边有权值（通过时间），对于每个节点有一个限制，即你每次只能在[2*K*ai,(2*K+1)ai)（K为任意实数）内从该节点离开。
思路：
裸的最短路，判断一下每次到达u这个节点时时a[u]的奇数倍还是偶数倍即可。
代码实现如下：
1 #include <set> 2 #include <map> 3 #include <queue> 4 #include <stack> 5 #include <cmath> 6 #include <bitset> 7 #include <cstdio> 8 #include <string> 9 #include <vector> 10 #include <cstdlib> 11 #include <cstring> 12 #include <iostream> 13 #include <algorithm> 14 using namespace std; 15 16 typedef long long LL; 17 typedef pair<LL, LL> pLL; 18 typedef pair<LL, int> pli; 19 typedef pair<int, LL> pil;; 20 typedef pair<int, int> pii; 21 typedef unsigned long long uLL; 22 23 #define lson i<<1 24 #define rson i<<1|1 25 #define lowbit(x) x&(-x) 26 #define IO ios::sync_with_stdio(false),cin.tie(0); 27 28 const double eps = 1e-8; 29 const int maxn = 1e6 + 7; 30 const double pi = acos(-1); 31 const int inf = 0x3f3f3f3f; 32 33 int t, n, m, tot, u, v, w, s, e; 34 int head[1007], vis[1007]; 35 LL a[1007]; 36 LL dis[1007]; 37 38 struct node { 39 int v, next; 40 LL w; 41 }ed[1007*1007 / 2]; 42 43 void addedge(int u, int v, LL w) { 44 ed[tot].v = v; 45 ed[tot].w = w; 46 ed[tot].next = head[u]; 47 head[u] = tot++; 48 ed[tot].v = u; 49 ed[tot].w = w; 50 ed[tot].next = head[v]; 51 head[v] = tot++; 52 } 53 54 void dij(int s) { 55 priority_queue<pli,vector<pli>,greater<pli> >q; 56 for(int i = 1; i <= n; i++) dis[i] = 1000000000; 57 dis[s] = 0; 58 q.push(make_pair(0, s)); 59 while(!q.empty()) { 60 int u = q.top().second; 61 q.pop(); 62 if(vis[u]) continue; 63 vis[u] = 1; 64 for(int i = head[u]; ~i; i = ed[i].next) { 65 int v = ed[i].v; 66 LL len = dis[u] + ed[i].w; 67 if(a[v] && v != e) { 68 int k = len / a[v]; 69 if(k & 1) len = (k + 1) * a[v]; 70 } 71 if(len < dis[v]) { 72 dis[v] = len; 73 q.push(make_pair(dis[v], v)); 74 } 75 } 76 } 77 } 78 79 int main() { 80 //FIN; 81 IO; 82 cin >>t; 83 while(t--) { 84 cin >>n >>m; 85 tot = 0; 86 memset(vis, 0, sizeof(vis)); 87 memset(head, -1, sizeof(head)); 88 for(int i = 1; i <= n; i++) { 89 cin >>a[i]; 90 } 91 for(int i = 1; i <= m; i++) { 92 cin >>u >>v >>w; 93 addedge(u, v, w); 94 } 95 cin >>s >>e; 96 dij(s); 97 cout <<dis[e] <<endl; 98 } 99 return 0; 100 }
G题题目：
题意：
求两个矩形面积交/面积并。
思路：
比赛时队友用扫描线过的，其实对于只有两个矩形，贪心即可。
代码实现如下：
1 #include <set> 2 #include <map> 3 #include <queue> 4 #include <stack> 5 #include <cmath> 6 #include <bitset> 7 #include <cstdio> 8 #include <string> 9 #include <vector> 10 #include <cstdlib> 11 #include <cstring> 12 #include <iostream> 13 #include <algorithm> 14 using namespace std; 15 16 typedef long long LL; 17 typedef pair<LL, LL> pLL; 18 typedef pair<LL, int> pli; 19 typedef pair<int, LL> pil;; 20 typedef pair<int, int> pii; 21 typedef unsigned long long uLL; 22 23 #define lson i<<1 24 #define rson i<<1|1 25 #define lowbit(x) x&(-x) 26 #define bug printf("********* "); 27 #define debug(x) cout<<"["<<x<<"]" <<endl; 28 #define FIN freopen("D://code//in.txt", "r", stdin); 29 #define IO ios::sync_with_stdio(false),cin.tie(0); 30 31 const double eps = 1e-8; 32 const LL mod = 1LL<<47; 33 const int maxn = 1e6 + 7; 34 const double pi = acos(-1); 35 const int inf = 0x3f3f3f3f; 36 37 int t; 38 int x1, yy1, w1, h1; 39 int x2, y2, w2, h2; 40 int x, y; 41 LL sum, ans; 42 43 int main() { 44 //FIN; 45 scanf("%d", &t); 46 while(t--) { 47 x = y = 0; 48 scanf("%d%d%d%d", &x1, &yy1, &w1, &h1); 49 scanf("%d%d%d%d", &x2, &y2, &w2, &h2); 50 sum = (LL)w1 * h1 + (LL)w2 * h2; 51 x = max(min(x1 + w1, x2 + w2) - max(x1, x2), 0); 52 y = max(min(yy1 + h1, y2 + h2) - max(yy1, y2), 0); 53 ans = (LL)x * y; 54 sum = sum - ans; 55 printf("%.2f ", 1.0 * ans / sum); 56 } 57 return 0; 58 }
H题题目：
题意：
以炉石传说为背景的题面，一个技能总共有n的伤害，可以将这n的伤害随机分配给敌方英雄和小兵，小兵的血量为m，英雄血量无穷，求杀死小兵的概率。
思路：
一眼公式，只是因为没玩过炉石传说，不懂它的技能时如何产生伤害的，问了才知道，这个技能是一滴一滴血进行减少的，也就是每一点伤害可以给英雄也可以给小兵，所以总的可能行为2^n，要想小兵死亡，则至少有m点伤害作用在小兵身上，所以可能性为：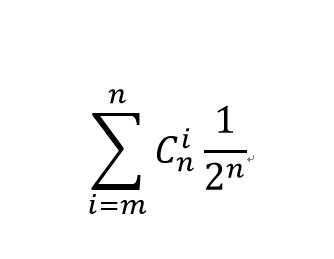
因为前段时间写过杭电多校一道题目（题目链接，题解链接），题目是要求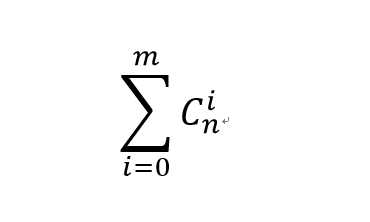
又我们知道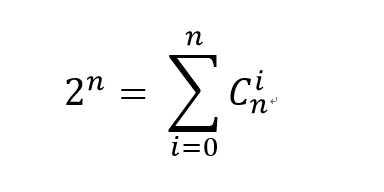
，因此我们本题可以借助那题的思路来写~（当然由于n，m的范围很小完全可以预处理出来所以的再求个前缀和。）
代码实现如下：
1 #include <set> 2 #include <map> 3 #include <queue> 4 #include <stack> 5 #include <cmath> 6 #include <bitset> 7 #include <cstdio> 8 #include <string> 9 #include <vector> 10 #include <cstdlib> 11 #include <cstring> 12 #include <iostream> 13 #include <algorithm> 14 using namespace std; 15 16 typedef long long ll; 17 typedef pair<ll, ll> pll; 18 typedef pair<ll, int> pli; 19 typedef pair<int, ll> pil;; 20 typedef pair<int, int> pii; 21 typedef unsigned long long ull; 22 23 #define lson i<<1 24 #define rson i<<1|1 25 #define IO ios::sync_with_stdio(false),cin.tie(0); 26 27 const double eps = 1e-8; 28 const int mod = 1e9 + 7; 29 const int maxn = 1e3 + 7; 30 const double pi = acos(-1); 31 32 int t, block; 33 ll sum; 34 ll a[maxn], b[maxn], pw[maxn], inv[maxn]; 35 36 struct node { 37 int l, r, id; 38 ll ans; 39 bool operator < (const node & x) const { 40 return (l - 1) / block == (x.l - 1) / block ? r < x.r : l < x.l; 41 } 42 }ask[maxn*100]; 43 44 ll Mod_Pow(ll x, ll n) { 45 ll res = 1; 46 while(n > 0) { 47 if(n & 1) res = res * x % mod; 48 x = x * x % mod; 49 n >>= 1; 50 } 51 return res; 52 } 53 54 void init() { 55 a[1] = 1; 56 pw[0] = 1; 57 for(int i = 1; i < maxn; i++) { 58 pw[i] = (pw[i-1] * 2) % mod; 59 inv[i] = Mod_Pow(pw[i], mod - 2); 60 } 61 for(int i = 2; i < maxn; i++) a[i] = a[i-1] * i % mod; 62 for(int i = 1; i < maxn; i++) b[i] = Mod_Pow(a[i], mod - 2); 63 } 64 65 ll C(int n, int m) { 66 if(n < 0 || m < 0 || m > n) return 0; 67 if(m == 0 || m == n) return 1; 68 return a[n] * b[n-m] % mod * b[m] % mod; 69 } 70 71 int main() { 72 //FIN; 73 ios::sync_with_stdio(false); 74 init(); 75 cin >>t; 76 block = sqrt(maxn); 77 sum = 1; 78 for(int i = 1; i <= t; i++) { 79 cin >>ask[i].l >>ask[i].r; 80 ask[i].r--; 81 ask[i].id = i; 82 } 83 sort(ask + 1, ask + t + 1); 84 for(int i = 1, l = 1, r = 0; i <= t; i++) { 85 while(l < ask[i].l) sum = (2 * sum - C(l++, r) + mod) % mod; 86 while(l > ask[i].l) sum = ((sum + C(--l, r)) * b[2]) % mod; 87 while(r < ask[i].r) sum = (sum + C(l, ++r)) % mod; 88 while(r > ask[i].r) sum = (sum - C(l, r--) + mod) % mod; 89 ask[ask[i].id].ans = ((pw[ask[i].l] - sum + mod) % mod * inv[ask[i].l]) % mod; 90 } 91 for(int i = 1; i <= t; i++) { 92 cout <<ask[i].ans <<endl; 93 } 94 return 0; 95 }
J题题目：
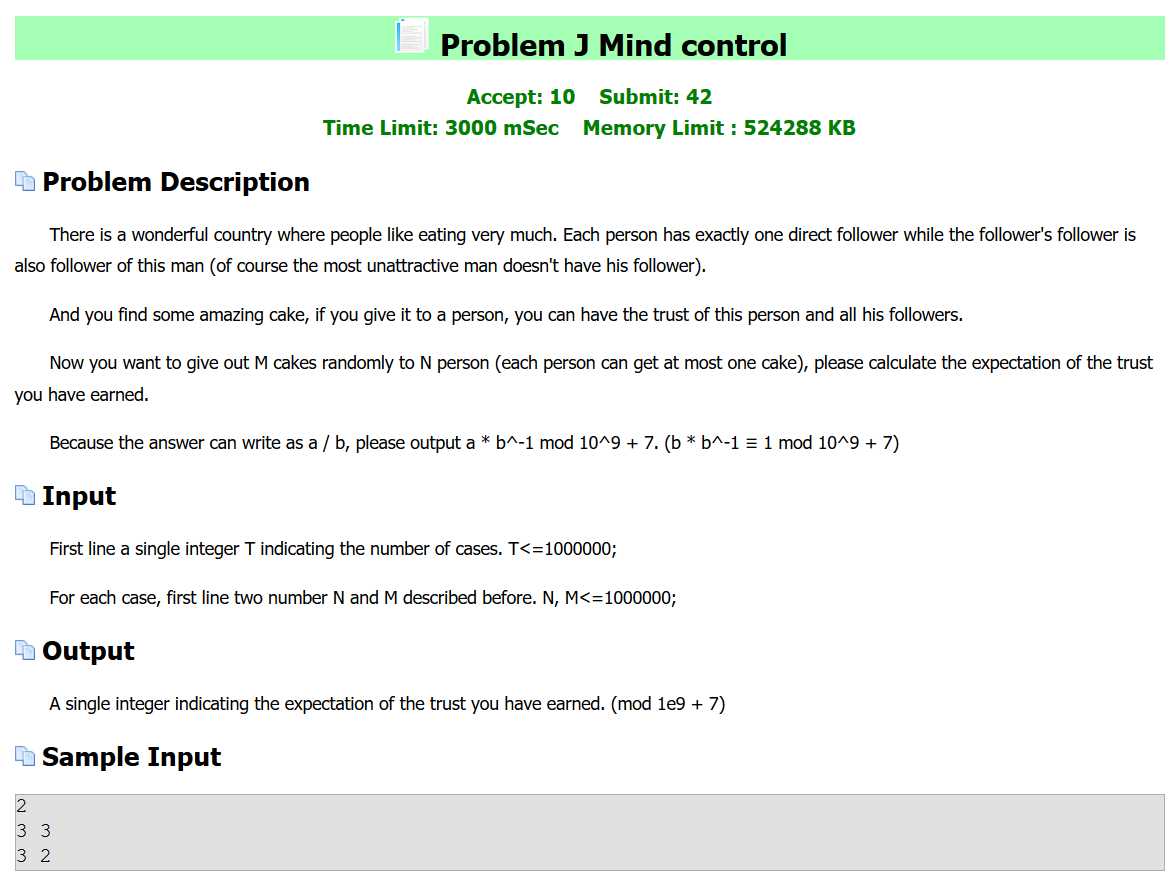
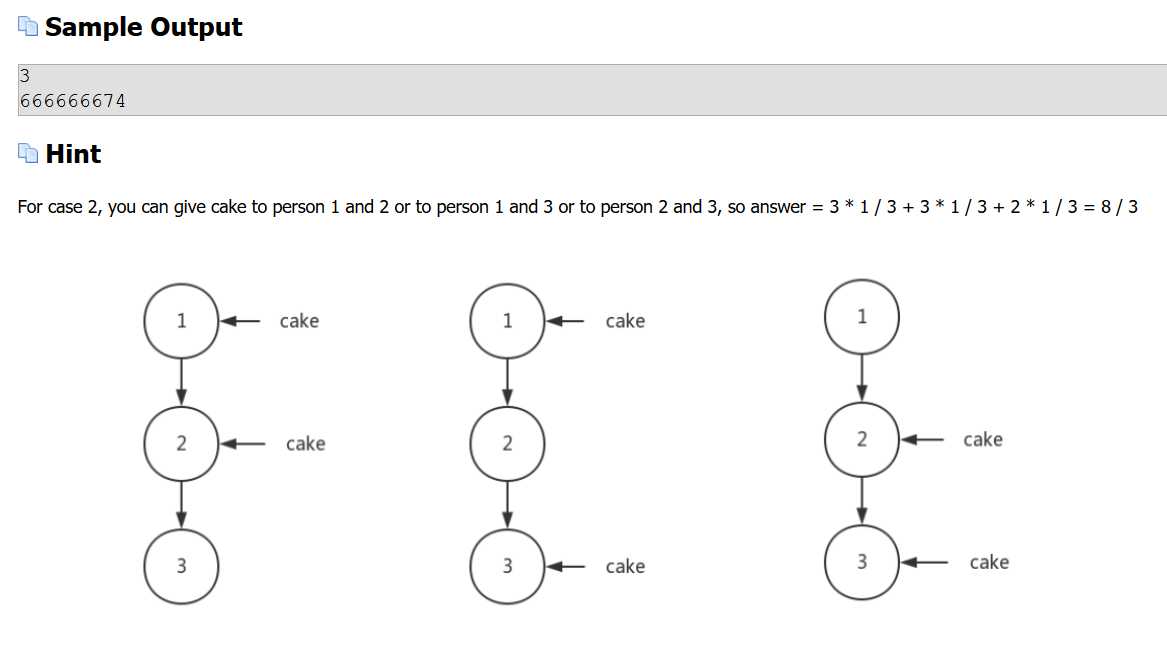
题意：
每个人（i）都有一个跟随者（i+1),跟随者的跟随者也是这个人的跟随者，以此类推。你有m个蛋糕，你将这m个蛋糕随机给这n个人，如果你给某一个人，那么那个人和他的跟随者都会对你诚实，最后求诚实人数的期望。
思路：
又是一眼公式题，但是化简极难……可能是我学的组合公式全学到狗身上去了吧，反正推了很久。
我们知道，如果我们将蛋糕给i，那么剩下的m-1个蛋糕你随便给i+1~n的人，都会获得n-i的诚实人数，那么我们枚举等级最高的人，给他一个蛋糕，剩下的m-1个蛋糕随便给等级比他低的即可，不能给等级比他高的人，不然会重复计算。
公式为：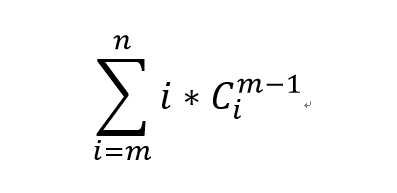
对于这个公式我们由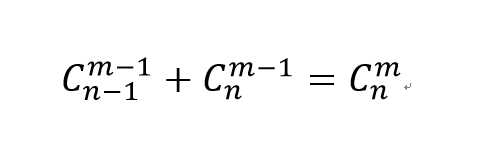
我们可以推得C(m,n-1)+C(m,n-2)+C(m,n-3)+...+C(m,m+1)+C(m,m) =C(m+1,n)，最后我们可以推得
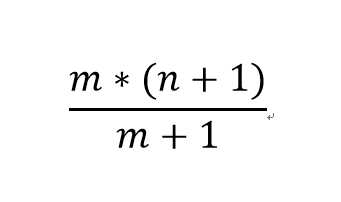，是不是很神奇？
代码实现如下：
1 #include <set> 2 #include <map> 3 #include <queue> 4 #include <stack> 5 #include <cmath> 6 #include <bitset> 7 #include <cstdio> 8 #include <string> 9 #include <vector> 10 #include <cstdlib> 11 #include <cstring> 12 #include <iostream> 13 #include <algorithm> 14 using namespace std; 15 16 typedef long long LL; 17 typedef pair<LL, LL> pLL; 18 typedef pair<LL, int> pli; 19 typedef pair<int, LL> pil;; 20 typedef pair<int, int> pii; 21 typedef unsigned long long uLL; 22 23 #define lson i<<1 24 #define rson i<<1|1 25 #define lowbit(x) x&(-x) 26 #define IO ios::sync_with_stdio(false),cin.tie(0); 27 28 const double eps = 1e-8; 29 const int mod = 1e9 + 7; 30 const int maxn = 1e6 + 7; 31 const double pi = acos(-1); 32 33 int t; 34 int inv[maxn]; 35 LL n, m, ans; 36 37 LL Mod_Pow(LL x, LL n) { 38 LL res = 1; 39 while(n) { 40 if(n & 1) res = res * x % mod; 41 x = x * x % mod; 42 n >>= 1; 43 } 44 return res; 45 } 46 47 void init() { 48 inv[1] = 1; 49 for(int i = 2; i < maxn; i++) { 50 inv[i] = Mod_Pow(i, mod - 2); 51 } 52 } 53 54 int main() { 55 init(); 56 scanf("%d", &t); 57 while(t--) { 58 scanf("%d%d", &n, &m); 59 if(m >= n) { 60 printf("%d ", n); 61 continue; 62 } 63 ans = (m * (n + 1) % mod) * inv[m+1] % mod; 64 printf("%lld ", ans); 65 } 66 return 0; 67 }
以上是关于第九届福建省大学生程序设计竞赛 2018.8.26组队训练赛的主要内容，如果未能解决你的问题，请参考以下文章
湖南省第九届大学生计算机程序设计竞赛 Interesting Calculator
“浪潮杯”第九届山东省ACM大学生程序设计竞赛重现赛 C-Cities