数据结构-单链表
Posted blog-yejy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构-单链表相关的知识,希望对你有一定的参考价值。
1. 单链表介绍
链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。
相比于顺序存储结构(一般指数组),链表在插入的时候可以达到O(1)的复杂度,如果你的数据容器需频繁进行插入删除操作,那链表是不错的选择。单向链表结构图如下所示:

2. 单链表常见问题汇总
链表是最基本的数据结构,在面试中,面试官也常常会选择链表来考察面试者的基本能力。主要由于链表的实现涉离不开指针,而指针往往又很容易出错,因此使得链表成为面试中一个比较好的考察点。
那这边是我从互联网上收集到的,在面试及生产中用的比较多的单链表知识点,具体如下:
(主要参考于 http://blog.csdn.net/luckyxiaoqiang/article/details/7393134#topic2)
1. 设计链表,实现链表基本的创建,添加,删除,查询操作
2. 合并两个有序链表
3. 反转链表
4. 删除链表的倒数第K个节点(k>0)
5. 查找链表的中间结点
6. 判断一个单链表中是否有环
7. 求两个单链表相交的第一个节点
8. 已知一个单链表中存在环,求进入环中的第一个节点
9. 给出一单链表头指针pHead和一节点指针pToBeDeleted,O(1)时间复杂度删除节点pToBeDeleted
3. 单链表基本实现(C++)
首先,我们实现一下对单链表的基本封装,具体代码如下: (编译平台:Linux centos 7.0 编译器:gcc 4.8.5 )
由于采用C++ 类进行封装,头节点不会提供给外部使用,因此对于处理多条链表关系,以及有环等问题,会专门用一节来整理,这些问题更偏向于提供一个解决问题的思路,偏算法,至于单链表数据结构,下面的封装基本可以满足。
头文件: single_list.h
#include <iostream>
/** @file single_list.h
*
* This is an list header file, implement single list warppes
*
* Created by yejy on 18-8-21
* copyright (c) yejy. all rights reserved
*
*/
#define INVALID_VALUE -1
struct _single_list_node
{
int dataEntry;
_single_list_node* Next;
};
/* single list */
class T_Single_List
{
typedef _single_list_node* Link_type;
public:
T_Single_List()
{
pHeadNode = new _single_list_node();
pHeadNode->Next = nullptr;
_size = 0;
}
~T_Single_List()
{
clear();
if(pHeadNode)
{
delete pHeadNode;
pHeadNode = nullptr;
}
_size = 0;
}
// head | data -> insert2 | data -> insert1 | data -> null
void InsertValueAtHead(int value) // 前插
{
if(pHeadNode)
{
Link_type pNode = new _single_list_node();
if(pNode)
{
pNode->dataEntry = value;
pNode->Next = pHeadNode->Next;
pHeadNode->Next = pNode;
++_size;
}
}
}
// head | data -> insert1 | data -> insert2 | data -> null
void InsertValueAtTail(int value) // 尾插
{
if(pHeadNode)
{
Link_type pNode = new _single_list_node();
Link_type pPollNode = pHeadNode; //
if(pNode)
{
// 单向链表实现尾插,需要遍历到最后一个节点插入
while(pPollNode->Next != nullptr)
{
pPollNode = pPollNode->Next;
}
pNode->Next = nullptr;
pNode->dataEntry = value;
pPollNode->Next = pNode;
++_size;
}
}
}
// 按序号插入
void InsertValueAtIndex(int index, int val)
{
if(index > _size || index <= 0)
{
std::cout << "error Not in range" << std::endl;
return ;
}
Link_type pPollNode = findbyindex(index);
Link_type pNode = new _single_list_node();
if(pNode)
{
pNode->Next = pPollNode->Next;
pPollNode->Next = pNode;
pNode->dataEntry = val;
++_size;
}
}
// 根据index删除
void deleteValueAtIndex(int index)
{
if(index > _size || index <= 0)
{
std::cout << "error Not in range" << std::endl;
return ;
}
Link_type pNode = findbyindex(index); //找到前一个
RemoveNext(pNode); //删除Next即可
}
// 根据index获取值
int GetValueByIndex(int index)
{
if(index > _size || index <= 0)
{
std::cout << "error Not in range" << std::endl;
return INVALID_VALUE;
}
Link_type pNode = findbyindex(index);
if(pNode->Next)
{
return pNode->Next->dataEntry;
}
return INVALID_VALUE;
}
// 修改值
void update(int value, int modify_value)
{
Link_type pNode = findbyvalue(value);
if(pNode->Next)
{
pNode->Next->dataEntry = modify_value;
}
}
// 查找链表的中间结点 使用快慢指针处理
// 一个step为1 另一个step为2
Link_type GetMidNode()
{
Link_type pNodeStep1 = pHeadNode;
Link_type pNodeStep2 = pHeadNode;
// while(pNodeStep2)
// {
// pNodeStep2 = pNodeStep2->Next;
// if(pNodeStep2)
// {
// pNodeStep2 = pNodeStep2->Next;
// }
// else
// {
// break;
// }
// pNodeStep1 = pNodeStep1->Next;
// }
while(pNodeStep2 && pNodeStep2->Next)
{
pNodeStep1 = pNodeStep1->Next;
pNodeStep2 = pNodeStep2->Next->Next;
}
return pNodeStep1;
}
// 求单链表反转 O(n)
void ReverseList()
{
if(pHeadNode->Next == nullptr)
{
return;
}
Link_type pNode = pHeadNode->Next->Next;
pHeadNode->Next->Next = nullptr;
_size = 1;
while(pNode)
{
Link_type pInsertNode = pNode;
pNode = pNode->Next;
pInsertNode->Next = pHeadNode->Next;
pHeadNode->Next = pInsertNode;
}
}
// 查找链表中倒数第k个节点的值( n - k + 1 )
int GetRePosNodeValue(int k)
{
if(k > _size || k <= 0)
{
std::cout << "error Not in range" << std::endl;
return INVALID_VALUE;
}
Link_type pNode = findbyindex(_size - k + 1);
if(pNode->Next)
{
return pNode->Next->dataEntry;
}
return INVALID_VALUE;
}
// 清空链表
void clear()
{
Link_type pNode = pHeadNode;
while(pNode->Next)
{
RemoveNext(pNode);
}
}
// 打印
void printf()
{
if(_size <= 0)
{
return;
}
Link_type pNode = pHeadNode->Next;
while(pNode)
{
std::cout << pNode->dataEntry << " ";
pNode = pNode->Next;
}
std::cout << std::endl;
}
private:
// 查找 (返回前一个指针)
Link_type findbyvalue(int value)
{
Link_type pNode = pHeadNode;
while(pNode)
{
if(pNode->Next && pNode->Next->dataEntry == value)
{
return pNode;
}
pNode = pNode->Next;
}
return nullptr;
}
Link_type findbyindex(int index)
{
int i = 0;
Link_type pNode = pHeadNode;
while(pNode) // 查找前一个
{
if(++i == index)
{
break;
}
pNode = pNode->Next;
}
return pNode;
}
void RemoveNext(Link_type pNode)
{
if(pNode->Next)
{
Link_type pNextNext = pNode->Next->Next;
delete pNode->Next;
pNode->Next = pNextNext;
--_size;
}
}
private:
Link_type pHeadNode; // 头节点指针
unsigned int _size; // 链表节点个数
};测试代码: main.h
#include "single_list.h"
int main(int argc, char * argv[])
{
T_Single_List link_list;
// 前插
link_list.InsertValueAtHead(1);
link_list.InsertValueAtHead(2);
link_list.InsertValueAtHead(3);
link_list.InsertValueAtHead(4);
link_list.InsertValueAtHead(5);
std::cout << "The link_list:";
link_list.printf();
T_Single_List link_list1;
// 尾插
link_list1.InsertValueAtTail(1);
link_list1.InsertValueAtTail(2);
link_list1.InsertValueAtTail(3);
link_list1.InsertValueAtTail(4);
link_list1.InsertValueAtTail(5);
std::cout << "The link_list1:";
link_list1.printf();
std::cout << "get link_list The third node: " << link_list.GetValueByIndex(3) << std::endl;
std::cout << "get link_list The RE sec node: " << link_list.GetRePosNodeValue(2) << std::endl;
std::cout << "get link_list The Mid node: " << link_list.GetMidNode()->dataEntry << std::endl;
std::cout << "get link_list1 The third node: " << link_list1.GetValueByIndex(3) << std::endl;
std::cout << "get link_list1 The RE sec node: " << link_list1.GetRePosNodeValue(2) << std::endl;
std::cout << "get link_list1 The Mid node: " << link_list1.GetMidNode()->dataEntry << std::endl;
std::cout << "The RE link_list:";
link_list.ReverseList();
link_list.printf();
std::cout << "The RE link_list1:";
link_list1.ReverseList();
link_list1.printf();
std::cout << "GetValueByIndex:";
std::cout << "get link_list1 The second node: " << link_list1.GetValueByIndex(2) << std::endl;
std::cout << "update:";
link_list1.update(2, 100);
link_list1.deleteValueAtIndex(1);
link_list1.printf();
link_list.clear();
link_list1.clear();
link_list.printf();
link_list1.printf();
return 0;
}测试结果:
bash-4.2$ ./single_list
The link_list:5 4 3 2 1
The link_list1:1 2 3 4 5
get link_list The third node: 3
get link_list The RE sec node: 2
get link_list The Mid node: 3
get link_list1 The third node: 3
get link_list1 The RE sec node: 4
get link_list1 The Mid node: 3
The RE link_list:1 2 3 4 5
The RE link_list1:5 4 3 2 1
GetValueByIndex:get link_list1 The second node: 4
update:4 3 100 1 4. 单链表热门问题
单链表定义:
// Definition for singly-linked list.
struct ListNode {
int val;
ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};1. 合并两个有序链表
解决思路类似于归并排序,边界情况,主要注意其中一个链表为空及两个链表都为空的情况,空间复杂度O(1),时间复杂度O(max(len1, len2))
实现代码
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
if(l1 == NULL)
{
return l2;
}
if(l2 == NULL)
{
return l1;
}
ListNode newNode(-1);
ListNode* pNode = &newNode;
while(l1 || l2)
{
if(l1 == NULL)
{
pNode->next = l2;
break;
}
if(l2 == NULL)
{
pNode->next = l1;
break;
}
if(l1->val > l2->val)
{
ListNode* pTemp = l2;
l2 = l2->next;
pTemp->next = pNode->next;
pNode->next = pTemp;
pNode = pNode->next;
}
else
{
ListNode* pTemp = l1;
l1 = l1->next;
pTemp->next = pNode->next;
pNode->next = pTemp;
pNode = pNode->next;
}
}
return newNode.next;
}2. 查找链表的中间结点
设置两个指针,两个指针同时向前走,一个走两步,一个走一步,当快指针到达链表末尾时,慢指针刚好到中间,刚好可以得到中间节点。空间复杂度O(1),时间复杂度O(n)
实现代码
ListNode* middleNode(ListNode* head) {
ListNode* pNodeStep1 = head; // slow 慢指针
ListNode* pNodeStep2 = head; // fast 快指针
while(pNodeStep2 && pNodeStep2->next)
{
pNodeStep2 = pNodeStep2->next->next;
pNodeStep1 = pNodeStep1->next;
}
return pNodeStep1;
}3. 求两个单链表相交的第一个节点
首先,我们遍历一下两个链表获取链表长度lengthA,lengthB。然后对于长度较长的链表,先向前走|lengthA-lengthB|的步数,接着两个链表一起往前走,直到找到第一个地址相同的节点,任务完成。空间复杂度O(1),时间复杂度O(n)
实现代码
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if(headA == NULL || headB == NULL)
{
return NULL;
}
int lengthA = 0;
int lengthB = 0;
ListNode *travelNodeA = headA;
ListNode *travelNodeB = headB;
while(travelNodeA)
{
++lengthA;
travelNodeA = travelNodeA->next;
}
while(travelNodeB)
{
++lengthB;
travelNodeB = travelNodeB->next;
}
travelNodeA = headA;
travelNodeB = headB;
// offset = |lengthB - lengthA|
int offset;
if(lengthB > lengthA)
{
offset = lengthB - lengthA;
while(offset > 0)
{
travelNodeB = travelNodeB->next;
--offset;
}
}
else
{
offset = lengthA - lengthB;
while(offset > 0)
{
travelNodeA = travelNodeA->next;
--offset;
}
}
while(travelNodeA)
{
if(travelNodeA == travelNodeB)
{
return travelNodeA;
}
travelNodeA = travelNodeA->next;
travelNodeB = travelNodeB->next;
}
return NULL;
}4. 给出一单链表头指针pHead和一节点指针pToBeDeleted,O(1)时间复杂度删除节点pToBeDeleted
主要思路,对于单链表,想要删除某个节点,那我们必须知道他的前一个节点,然后通过改变前一个节点的next指针来将该节点删除,而又因为链表中保存的dataEntry结构是一样的 ,都为整形,因此我们可以将该节点和他的后一个节点数据进行交换,使得该节点变成前一个节点,接着通过删除后一个节点的方式,即完成了该节点的删除。空间复杂度O(1),时间复杂度O(1)
实现代码
void deleteNode(ListNode* node) {
if(node == NULL || node->next == NULL)
{
return;
}
ListNode* pNode = node->next;
node->val = pNode->val;
node->next = pNode->next;
delete pNode;
pNode = NULL;
}5. 链表成环的问题
1. 判断一个链表中是否有环存在
主要思路,也是使用两个指针去遍历,一个指针一次走两步,一个指针一次走一步,如果有环,两个指针肯定会在环中相遇。空间复杂度O(1),时间复杂度O(1)
实现代码
bool hasCycle(ListNode *head) {
if(head == NULL || head->next == NULL)
{
return false;
}
ListNode *step1Node = head; // slow
ListNode *step2Node = head; // fast
while(step2Node && step2Node->next)
{
step2Node = step2Node->next->next;
step1Node = step1Node->next;
if(step2Node == step1Node)
{
return true;
}
}
return false;
}2. 如果存在环,找出环的入口点;
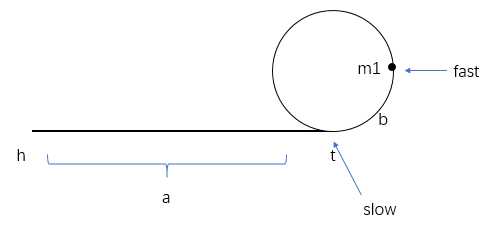
对于链表成环的问题,最关键的一点就在于如何获取到环的入口点,如果获取到了,那关于环的各种信息,都可以很容易的得到,那么,我们来分析一下入口节点的获取思路
我们使用快慢节点可以知道链表是否有环,因为快慢节点一直往前走的话,是肯定会相遇的,但是具体相遇在哪里,入口点是哪里呢,首先我们可以确定的一点是,慢指针在跑完一圈的过程中,快指针是肯定会和慢指针相遇的,因为快指针速度是慢指针的两倍,想象一下如果所有节点都在环内,那就和跑圈是一样的了,跑圈最终是在起点的地方相遇,示意图则是过程中相遇。
那么我们在这个前提下进行分析,根据示意图,我们假设图中 m1 为相遇点,那慢节点走过的距离为 a+b,这个时候快节点绕圈多少次呢,我们不知道,假设为 n 次,环一周距离为 k,那我们可以得出这个等式:
(a + b) * 2 = a + b + n * k (慢指针跑过距离的两倍等于快指针跑过的距离)
我们对等式变一下形,因为我们要求入口节点,那么首先需要得到 a 的等式分析一下
a = n * k - b
好像还是看不出来,只知道 a+b 刚好等于一圈的 n 倍,我们再换个样子看一下
a = (n-1) * k + (k - b)
那现在呢,因为我们链表是顺一个方向走的,而 a 的距离刚好是从头节点到入口点的距离,而 k - b,刚好是相遇点,走到入口点的距离,因为我们在实现链表是否成环中已经找到了相遇点,那么我们改变一下思路,我们不走两步,走一步,让一个指针从相遇点开始一步一步往前走,让另一个指针从头节点开始一步一步往前走,最后是不是在入口点就相遇了,只是相遇点开始走的那个指针可能是多次经过了入口点而已。
实现代码
ListNode *detectCycle(ListNode *head) {
if(head == NULL || head->next == NULL)
{
return NULL;
}
ListNode *step1Node = head; // slow
ListNode *step2Node = head; // fast
while(step2Node && step2Node->next)
{
step2Node = step2Node->next->next;
step1Node = step1Node->next;
if(step2Node == step1Node)
{
ListNode *startNode = head;
ListNode *meetNode = step1Node;
while(startNode)
{
if(meetNode == startNode)
{
return meetNode;
}
startNode = startNode->next;
meetNode = meetNode->next;
}
}
}
return NULL;
}实现都是这两天在leetcode上刷的,有关链表的问题上面基本都有,如果想要锻炼一下的话,可以去上面尝试一下!!
2018年8月25日23:16:37
以上是关于数据结构-单链表的主要内容,如果未能解决你的问题,请参考以下文章