Count Numbers(矩阵快速幂)

Posted 2021-01-01 lglh

Count Numbers

时间限制: 8 Sec  内存限制: 128 MB
提交: 43  解决: 19
[提交] [状态] [讨论版] [命题人:admin]

题目描述

Now Alice wants to sum up all integers whose digit sum is exactly ab .
However we all know the number of this kind of integers are unlimited. So she decides to sum up all these numbers whose each digit is non-zero.
Since the answer could be large, she only needs the remainder when the answer divided by a given integer p.

 

输入

The input has several test cases and the ?rst line contains the integer t (1 ≤ t ≤ 400) which is the number of test cases.
For each test case, a line consisting of three integers a, b (1 ≤ a, b ≤ 20) and p (2 ≤ p ≤ 109 ) describes the restriction of the digit sum and the given integer p.

 

输出

For each test case, output a line with the required answer.
Here we provide an explanation of the following sample output. All integers satisfying the restriction in the input are 4, 13, 31, 22, 121, 112, 211 and 1111. The sum of them all is 4 + 13 + 31 + 22 + 121 + 112 + 211 + 1111 = 1625 and that is exactly the sample output.

 

样例输入

5
2 1 1000000
3 1 1000000
2 2 1000000
3 3 1000000
10 1 1000000

 

样例输出

13
147
1625
877377
935943

 

题意：求十进制下各个位上的数字和为n的数的总和。
分析：n很大，要用__int128来存。如果这个数的最后一位为1，那么就需要求出所有k-1的答案数字，然后在其最后加上1，如果最后一位为2，那么就需要求出所有k-2的答案数字，然后在其最后加上2，、、、、、、，
一直可以分析到最后一位为9的情况。那么我们需要两个数组ans[i],cut[i]，ans[i]代表n=i时的答案是多少，cut[i]代表n=i时满足数字和是i的数字有多少个。因此就可以推出递推公式：cut[i]=sum(cut[i-j]){1<=j<=9},ans[i]=sum(10*ans[i-j]+j*cut[i-j]){1<=j<=9}。
有了递推式就可以套矩阵快速幂了，这里要注意矩阵要开18*18的，这样方便转移状态。
最后一点就是矩阵乘法可以放弃以往的一行乘一列的写法，用一种新的写法，这样可以省下不少时间。
构造的矩阵（n大于9时，用于以n==9的为基础往上递推，n小于等于9时直接暴力）为：

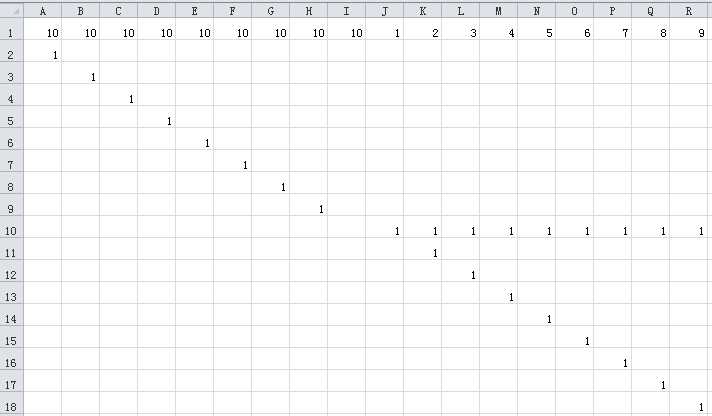
AC代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll p;
int addmod(int a,int b)
{
    return a+b>=p?a+b-p:a+b;
}
int mulmod(long long a,int b)
{
    return a*b%p;
}
struct Mat
{
    int v[18][18];
    Mat()
    {
        memset(v,0,sizeof(v));
    }
    void init()
    {
        for(int i=0;i<18;i++)
        {
            v[i][i]=1;
        }
    }

};
Mat operator *(Mat a,Mat b)
{
    Mat c;
    for (int i=0; i<18; i++)
    {
        for (int j=0; j<18; j++)
        {
            if(a.v[i][j])
            {
                for (int k=0; k<18; k++)
                {
                    if(b.v[j][k])
                    {
                        c.v[i][k]=addmod(c.v[i][k],mulmod(a.v[i][j]%p,b.v[j][k]%p));
                    }
                }
            }
        }
    }
    return c;
}
Mat qmod(Mat a,__int128 k)
{
    Mat c;
    c.init();
    while(k>0)
    {
        if(k&1) c=c*a;
        a=a*a;
        k>>=1;
    }
    return c;
}
int main()
{
    ll ans[15]={0},cut[15]={0};
    ll aa,bb,t;
    __int128 now;
    Mat a,b,c;
    cut[0]=1;
    for(int i=1; i<=9; i++)
    {
        for(int j=1; j<=i; j++)
        {
            ans[i]+=10*ans[i-j]+j*cut[i-j];
            cut[i]+=cut[i-j];
        } 
    }
    for(int i=0; i<9; i++) a.v[0][i]=10;
    for(int i=9; i<18; i++) a.v[0][i]=i-8;
    for(int i=1; i<9; i++) a.v[i][i-1]=1;
    for(int i=9; i<18; i++) a.v[9][i]=1;
    for(int i=10; i<18; i++) a.v[i][i-1]=1;
    scanf("%lld",&t);
    while(t--)
    {
        scanf("%lld %lld %lld",&aa,&bb,&p);
        for(int i=0; i<9; i++) b.v[i][0]=ans[9-i]%p;
        for(int i=9; i<18; i++) b.v[i][0]=cut[18-i]%p;
        now=aa;
        for(int i=2; i<=bb; i++) now=now*(__int128)aa;
        if(now<=9)
        {
            printf("%lld
",ans[now]%p);
            continue;
        }
        c=qmod(a,now-9)*b;
        printf("%lld
",c.v[0][0]);
    }
    return 0;
}

View Code

注意：__int128在有的情况下不能编译！！！