栈 1044 题解

Posted 2021-01-01 lixiao189

题意：

问如果有一个序列为1到$ n $ 通过不同的操作得到的出栈序列有几个？

思路

假如有下面这个图。

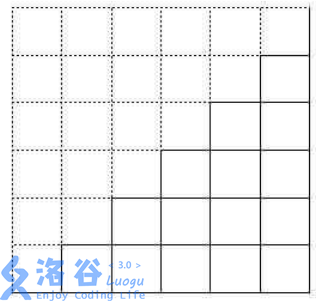
我们把一个数出栈看成是往上走一步，入栈往右走一步那么（注意是格点）我们从点 $ (1,1) $ 到达 $ (n,n) $ 的方案数就是所求答案。注意由于我们出栈的数量不能大于出栈的数量，所以我们走到的点 $ (i,j) $ 必须要满足 $ i le j $
。我们设到达 $ (i,j) $ 的方案数为 $ dp_{i,j} $ 那么显然有dp方程 $ dp_{i,j}=dp_{i-1,j}+dp_{i,j-1} $ 最后注意一下边界，和特殊处理一下边缘就可以了。

注意：

我们知道这个东西最后算出来的东西是很大的，所以我们一定要记得开 long long

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 20;

long long n;
long long dp[N][N];

int main(){
    scanf("%lld",& n);
    
    for(register int j=1;j<=n+1;j++){
        for(register int i=1;i<=j;i++){
            if(i==1 && j==1) dp[i][j]=1;
            else if(i==1) dp[i][j]=dp[i][j-1];
            else if(i==j) dp[i][j]=dp[i-1][j];
            else dp[i][j]=dp[i-1][j]+dp[i][j-1];
        }
    }
    
    printf("%lld
",dp[n+1][n+1]);
    
    return 0;
}