跟我学算法-pca(降维)

Posted 2021-01-01 my-love-is-python

pca是一种黑箱子式的降维方式，通过映射，希望投影后的数据尽可能的分散， 因此要保证映射后的方差尽可能大，下一个映射的方向与当前映射方向正交

pca的步骤：

第一步: 首先要对当前数据(去均值)求协方差矩阵，协方差矩阵= 数据*数据的转置/(m-1) m表示的列数，对角线上表示的是方差，其他位置表示的是协方差

第二步：需要通过矩阵对角化，使得协方差为0，只存在对角线方向的数据，这个时候就能得到我们的特征值和特征向量

第三步： 将当前数据*特征向量就完成了降维工作,特征值/特征值之和, 可以表示特征值对应特征向量的表达重要性

下面是程序的说明

第一步：数据导入， 去均值， 求协方差

import pandas as pd
import  numpy as np
import matplotlib.pyplot as plt

df = pd.read_csv(‘iris.data‘)
print(df.head())

df.columns=[‘sepal_len‘, ‘sepal_wid‘, ‘petal_len‘, ‘petal_wid‘, ‘class‘]
print(df.head())

# 用来储存变量
X = df.ix[:, 0:4].values
#用来储存标签
y = df.ix[:, 4].values   

msg ={‘Iris-setosa‘:0, ‘Iris-versicolor‘:1, ‘Iris-virginica‘:2}
df[‘class‘] = df[‘class‘].map(msg)  #把字母换成数字

#进行标准化
from sklearn.preprocessing import StandardScaler
Scaler = StandardScaler()
X_Scaler = Scaler.fit_transform(X)

# 求每一行的均值
mean_vec = np.mean(X_Scaler, axis=0)
#去均值后求协方差矩阵
cov_mat = (X_Scaler-mean_vec).T.dot(X_Scaler-mean_vec)/(X_Scaler.shape[0]-1)
print(cov_mat)
#使用np求协方差矩阵,结果是一样的
cov_mat = np.cov(X_Scaler.T)
print(cov_mat)

第二步：求矩阵对角化的过程，就是一个求特征值和特征向量的过程

# 求特征值和特征向量
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
print(eig_vals, eig_vecs)

#将特征值与特征向量合并
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:, i]) for i in range(len(eig_vals))] #组合对应
eig_pairs.sort(key=lambda x:x[0], reverse=True)


tot = sum(eig_vals)

var_exp = [(i/tot)*100 for i in sorted(eig_vals, reverse=True)]
#cumsum表示每前两个数相加
cum_var_exp = np.cumsum(var_exp)
#画图
plt.figure(figsize=(6, 4))
#画柱状图
plt.bar(range(4), var_exp, alpha=0.5, align=‘center‘,
            label=‘individual explained variance‘)
#画步阶图
plt.step(range(4), cum_var_exp, where=‘mid‘,
             label=‘cumulative explained variance‘)
plt.ylabel(‘Explained variance ratio‘)
plt.xlabel(‘Principal components‘)
plt.legend(loc=‘best‘)
plt.tight_layout()

第三步：将数据(去均值)

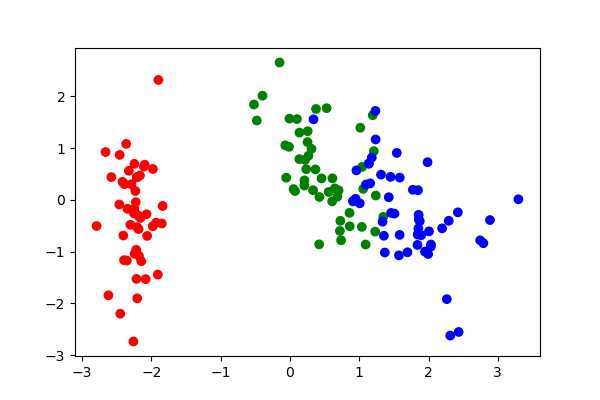
#把4维矩阵降低到两维，取前两个特征向量组合转置点乘即可

#np.hstack合并两个向量,reshape让一行变成一列,相当于转置
matrix_w = np.hstack((eig_pairs[0][1].reshape(4,1),
                      eig_pairs[1][1].reshape(4,1)))


#变换以后的矩阵149*4 .dot 4*2 = 149*2
become_X_Scaler = X_Scaler.dot(matrix_w)
print(become_X_Scaler)
plt.figure(figsize=(6, 4))

color = np.array([‘red‘, ‘green‘, ‘blue‘]) #构成行列式
plt.scatter(become_X_Scaler[:,0], become_X_Scaler[:,1], c=color[df[‘class‘]])  #画出种类对应颜色的散点图
plt.show()