PAT 1065 A+B and C[大数运算][溢出]

Posted 2021-01-01 bluebluesea

1065 A+B and C (64bit)（20 分）

Given three integers A, B and C in [?2?63??,2?63??], you are supposed to tell whether A+B>C.

Input Specification:

The first line of the input gives the positive number of test cases, T (≤10). Then T test cases follow, each consists of a single line containing three integers A, B and C, separated by single spaces.

Output Specification:

For each test case, output in one line Case #X: true if A+B>C, or Case #X: false otherwise, where X is the case number (starting from 1).

Sample Input:

3
1 2 3
2 3 4
9223372036854775807 -9223372036854775808 0

Sample Output:

Case #1: false
Case #2: true
Case #3: false

 题目大意：给出三个数，判断前两个数的和是否>第三个数，数是非常大的，需要用字符串来处理的。

 //这里需要认真学习大数加法与大数乘法的套路。

//看了题解之后，才发现根本不是，long long就是2^64！！！

//这个为溢出问题，

代码来自：https://www.liuchuo.net/archives/2023

#include <cstdio>
using namespace std;
int main() {
    int n;
    scanf("%d", &n);
    for(int i = 0; i < n; i++) {
        long long a, b, c;
        scanf("%lld %lld %lld", &a, &b, &c);
        long long sum = a + b;
        if(a > 0 && b > 0 && sum < 0) {//此时产生溢出，A+B>C
            printf("Case #%d: true
", i + 1);
        } else if(a < 0 && b < 0 && sum >= 0){//产生溢出，说明64位表示不了这么小的数，
            printf("Case #%d: false
", i + 1);//那么一定是小于。
        } else if(sum > c) {//其他为正常情况
            printf("Case #%d: true
", i + 1);
        } else {
            printf("Case #%d: false
", i + 1);
        }
    }
    return 0;
}

 

//我发现我很不理解，这个表示范围的问题，所以学习了一下：https://blog.csdn.net/y12345678904/article/details/52854230#commentBox

对于int 来说，4个字节，32位，有一位是符号为，那么它表示的数的范围就是（-2^31,2^31-1）。

右边的很好理解，比如4位，除去一位符号位，最大正数能表示7，（2^3-1）.

那么对于最小数呢？由于负数在计算机中是用补码（原码取反+1）来存的，

-1的原码：1000 0000 0000 0000 0000 0000 0000 0001；

-1的补码：1111 1111 1111 1111 1111 1111 1111 1111；

-2147483647（-2^31+1）原码：1111 1111 1111 1111 1111 1111 1111 1111；

-2147483647补码：1000 0000 0000 0000 0000 0000 0000 0001；

但是！零有二进制中+0和-0两种形式：

+0原码为：0000 0000 0000 0000 0000 0000 0000 0000；

-0原码为：1000 0000 0000 0000 0000 0000 0000 0000；

那么就将-0拿来作为了-2^31,所以就是这么来的！

-2147483648的补码表示为1000 0000 0000 0000 0000 0000 0000 0000，在32位没有原码。

注意，这个补码并不是真正的补码，真正的补码（原码也是这个）是1 1000 0000 0000 0000 0000 0000 0000 0000，溢出（已经多了一位1，！不是32位能表示的了！）。

溢出情况：https://blog.csdn.net/diffjd/article/details/72835698

比如1字节为例：

正数区间：0000 0001 ~ 0111 1111  (1~127)

负数区间：1000 0000 ~ 1111 1111（-1~-127）

并且规定将-0表示为-128，那么如果最大整数超过产生溢出怎么办？

写了一个：

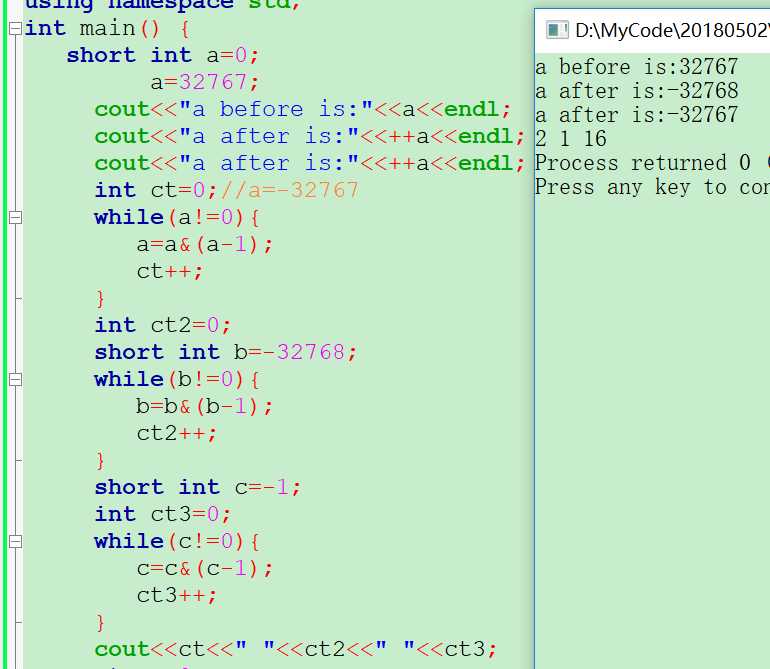
对图中a的二进制：0111 1111 1111 1111，此时再加就会超出界限，1000 0000 0000 0000，此时就是溢出了，就变为了负数，

此时：-32768在计算机中的表示就是-0，也就是1000 0000 0000 0000，那么在此基础上再做++运算，在计算机中补码是直接进行加法运算的，

结果就是1000 0000 0000 0001（对应的原码是：1111 1111 1111 1111），对应的十进制就是-32767.

 终于搞明白了！

如图中的最后一行三个数：

其中2表示-32767中有两个1，包括符号位1和最后一位1；

其中1表示-32768中有一个1，即符号为的1；

其中16表示-1中有16个1，全为1.

这个运行结果再一次的证明了，会变成整数，是直接进行补码运算的。

//终于搞明白了！