UVA806-Spatial Structures(四分树)

Posted 2020-12-31 npugen

Problem UVA806-Spatial Structures

Accept：329  Submit：2778

Time Limit: 3000 mSec

Problem Description

 

 

 

 Input

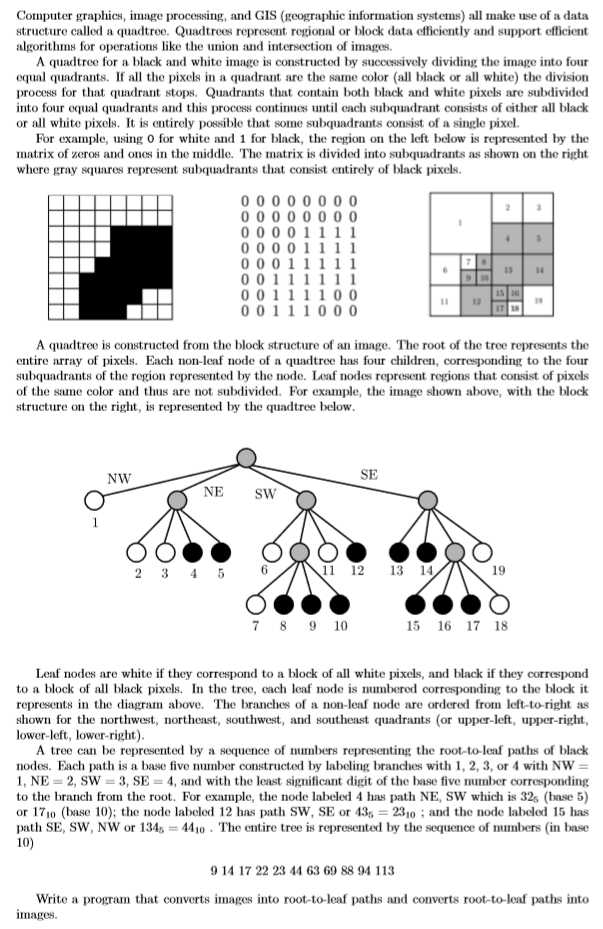
The input contains one or more images. Each image is square, and the data for an image starts with an integer n, where |n| is the length of a side of the square (always a power of two, with |n| < 64) followed by a representation of the image. A representation is either a sequence of n2 zeros and ones comprised of |n| lines of |n| digits per line, or the sequence of numbers that represent the root-to-leaf paths of each black node in the quadtree that represents the image. If n is positive, the zero/one representation follows; if n is negative, the sequence of black node path numbers (in base 10) follows. The sequence is terminated by the number -1. A one-node tree that represents an all-black image is represented by the number 0. A one-node tree that represents an all-white image is represented by an empty sequence (no numbers). The end of data is signaled by a value of 0 for n.

 

 Output

For each image in the input, ?rst output the number of the image, as shown in the sample output. Then output the alternate form of the image. If the image is represented by zeros and ones, the output consists of root-to-leaf paths of all black nodes in the quadtree that represents the image. The values should be base 10 representations of the base 5 path numbers, and the values should be printed in sorted order. If there are more than 12 black nodes, print a newline after every 12 nodes. The total number of black nodes should be printed after the path numbers. If the image is represented by the root-to-leaf paths of black nodes, the output consists of an ASCII representation of the image with the character ‘.’ used for white/zero and the character ‘*’ used for black/one. There should be n characters per line for an n×n image.

 

 Sample Input

8

00000000

00000000

00001111

00001111

00011111

00111111

00111100

00111000

-8

9 14 17 22 23 44 63 69 88 94 113 -1

2

00

00

-4

0 -1

0

 

 Sample Ouput

Image 1

9 14 17 22 23 44 63 69 88 94 113

Total number of black nodes = 11
Image 2

........

........

....****

....****

...*****

..******

..****..

..***...
Image 3

Total number of black nodes = 0
Image 4

****

****

****

****

 

题解：这个题如果没有lrj前面例题的铺垫，我自己估计是搞不定，不过做了那个例题之后，这个题就是稍微麻烦一点，没什么特殊的地方，重在代码基本功。

这个题的输出格式有点坑，总的来说就是题中没说的换行不要有，尤其是最后一个Case。

四分树例题：UVA297：Quadtrees

 

  1 #include <iostream>
  2 #include <cstdio>
  3 #include <cstring>
  4 #include <cstdlib>
  5 #include <string>
  6 #include <vector>
  7 #include <algorithm>
  8 using namespace std;
  9 
 10 const int maxn = 70;
 11 int n,cnt;
 12 char gra[maxn][maxn];
 13 vector<int> ans;
 14 
 15 bool is_black(int r,int c,int wide){
 16     for(int i = r;i < r+wide;i++){
 17         for(int j = c;j < c+wide;j++){
 18             if(gra[i][j] == ‘0‘) return false;
 19         }
 20     }
 21     return true;
 22 }
 23 
 24 bool is_white(int r,int c,int wide){
 25     for(int i = r;i < r+wide;i++){
 26         for(int j = c;j < c+wide;j++){
 27             if(gra[i][j] == ‘1‘) return false;
 28         }
 29     }
 30     return true;
 31 }
 32 
 33 int consumption(string &ss){
 34     int res = 0;
 35     for(int i = ss.size()-1;i >= 0;i--){
 36         res *= 5;
 37         res += ss[i]-‘0‘;
 38     }
 39     return res;
 40 }
 41 
 42 void cal(string str,int r,int c,int wide){
 43     if(is_black(r,c,wide)){
 44         ans.push_back(consumption(str));
 45         return;
 46     }
 47     else if(is_white(r,c,wide)) return;
 48     else{
 49         cal(str+"1",r,c,wide/2);
 50         cal(str+"2",r,c+wide/2,wide/2);
 51         cal(str+"3",r+wide/2,c,wide/2);
 52         cal(str+"4",r+wide/2,c+wide/2,wide/2);
 53     }
 54 }
 55 
 56 int solve(int n){
 57     cnt = 0;
 58     ans.clear();
 59     for(int i = 0;i < n;i++){
 60         scanf("%s",gra[i]);
 61     }
 62     string str = "";
 63     if(is_black(0,0,n)) return 1;
 64     if(is_white(0,0,n)) return -1;
 65     cal(str+"1",0,0,n/2);
 66     cal(str+"2",0,n/2,n/2);
 67     cal(str+"3",n/2,0,n/2);
 68     cal(str+"4",n/2,n/2,n/2);
 69     return 0;
 70 }
 71 
 72 vector<int> num;
 73 
 74 void converse(int val,string &ss){
 75     while(val){
 76         ss += (val%5+‘0‘);
 77         val /= 5;
 78     }
 79 }
 80 
 81 void draw(string &ss,int pos,int r,int c,int wide){
 82     if(pos == ss.size()){
 83         for(int i = r;i < r+wide;i++){
 84             for(int j = c;j < c+wide;j++){
 85                 gra[i][j] = ‘*‘;
 86             }
 87         }
 88         return;
 89     }
 90     if(ss[pos] == ‘1‘){
 91         draw(ss,pos+1,r,c,wide/2);
 92     }
 93     else if(ss[pos] == ‘2‘){
 94         draw(ss,pos+1,r,c+wide/2,wide/2);
 95     }
 96     else if(ss[pos] == ‘3‘){
 97         draw(ss,pos+1,r+wide/2,c,wide/2);
 98     }
 99     else draw(ss,pos+1,r+wide/2,c+wide/2,wide/2);
100 }
101 
102 void solve2(int n){
103     int x;
104     num.clear();
105     memset(gra,0,sizeof(gra));
106     while(scanf("%d",&x) && x!=-1) num.push_back(x);
107     if(num.size()==1 && num[0]==0){
108         for(int i = 0;i < n;i++){
109             for(int j = 0;j < n;j++){
110                 printf("*");
111             }
112             printf("
");
113         }
114         return;
115     }
116     for(int i = 0;i < num.size();i++){
117         string ss = "";
118         converse(num[i],ss);
119         draw(ss,0,0,0,n);
120     }
121     for(int i = 0;i < n;i++){
122         for(int j = 0;j < n;j++){
123             if(gra[i][j] == ‘*‘) printf("%c",gra[i][j]);
124             else printf(".");
125         }
126         printf("
");
127     }
128 }
129 
130 int iCase = 1;
131 
132 int main()
133 {
134     //freopen("input.txt","r",stdin);
135     //freopen("output.txt","w",stdout);
136     bool flag = false;
137     while(~scanf("%d",&n) && n){
138         if(flag) printf("
");
139         flag = true;
140         if(n > 0){
141             int flag = solve(n);
142             printf("Image %d
",iCase++);
143             if(flag == 1){
144                 printf("%d
",0);
145                 printf("Total number of black nodes = %d
",1);
146             }
147             else if(flag == -1){
148                 printf("Total number of black nodes = %d
",0);
149             }
150             else{
151                 sort(ans.begin(),ans.end());
152                 int cnt = 0;
153                 for(int i = 0;i < ans.size();i++){
154                     if(cnt == 0) printf("%d",ans[i]);
155                     else printf(" %d",ans[i]);
156                     cnt++;
157                     if(cnt == 12) cnt = 0,printf("
");
158                 }
159                 if(ans.size()%12)printf("
");
160                 printf("Total number of black nodes = %d
",ans.size());
161             }
162         }
163         else{
164             printf("Image %d
",iCase++);
165             solve2(-n);
166         }
167     }
168     return 0;
169 }