FWT 入门

Posted 2020-12-31 ccut-ry

 

 

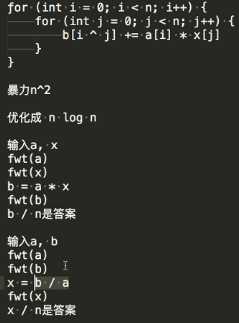
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const ll maxn = 3e5+5;
const ll mod = 1e9+7;

ll n;
ll a[maxn], b[maxn];
void fwt(ll *a)
{
    for(ll d=1;d<n;d<<=1)
        for(ll m=d<<1,i=0;i<n;i+=m)
            for(ll j=0;j<d;j++)
            {
                ll x=a[i+j],y=a[i+j+d];
                a[i+j]=(x+y)%mod,a[i+j+d]=(x-y+mod)%mod;
                //xor:a[i+j]=x+y,a[i+j+d]=x-y;
                //and:a[i+j]=x+y;
                //or:a[i+j+d]=x+y;
            }
}

ll qw(ll a, ll b){
	ll res = 1;
	while(b){
		if (b&1) res = res*a%mod;
		a = a*a%mod;
		b >>= 1;
	}
	return res;
}

int main () {
	cin >> n;
	
	for(ll i = 0; i < n; i++){
		scanf("%lld", &a[i]);
	}	
	for(ll i = 0; i < n; i++){
		scanf("%lld", &b[i]);
	}
	fwt(a); fwt(b);
	for(ll i = 0; i < n; i++){
		if (a[i] != 0){
			b[i] = b[i]*qw(a[i], mod-2)%mod;
		}
	}
	fwt(b);
	for(ll i = 0; i < n; i++){
		b[i] = b[i]*qw(n, mod-2)%mod;
		printf("%lld
", b[i]);
	}
	
	return 0;
}