数据分析 第四篇：聚类分析（划分）

Posted 2020-12-31 ljhdo

聚类是把一个数据集划分成多个子集的过程，每一个子集称作一个簇（Cluster），聚类使得簇内的对象具有很高的相似性，但与其他簇中的对象很不相似，由聚类分析产生的簇的集合称作一个聚类。在相同的数据集上，不同的聚类算法可能产生不同的聚类。

聚类分析用于洞察数据的分布，观察每个簇的特征，进一步分析特定簇的特征。由于簇是数据对象的子集合，簇内的对象彼此相似，而与其他簇的对象不相似，因此，簇可以看作数据集的“隐性”分类，聚类分析可能会发现数据集的未知分组。

聚类通过观察学习，不需要提供每个训练元素的隶属关系，属于无监督式学习（unspervised learning），主要的聚类算法可以分为以下四类：

• 划分聚类（Partitioning Clustering）
• 层次聚类（Hierarchical clustering）
• 基于密度的方法
• 基于网格的方法

本文简单介绍最简单的划分聚类算法，划分聚类是指：给定一个n个对象的集合，划分方法构建数据的k个分组，其中，每个分区表示一个簇，并且 k<= n，也就是说，把数据划分为k个组，使得每个组至少包含一个对象，基本的划分方法采取互斥的簇划分，这使得每个对象都仅属于一个簇。为了达到全局最优，基于划分的聚类需要穷举所有可能的划分，计算量极大，实际上，常用的划分方法都采用了启发式方法，例如k-均值（k-means）、k-中心点(k-medoids），渐进地提高聚类质量，逼近局部最优解，启发式聚类方法比较适合发现中小规模的球状簇。

一，k-均值

k-均值（kmeans）是一种基于形心的计数，每一个数据元素的类型是数值型，k-均值算法把簇的形心定义为簇内点的均值，k-均值算法的过程：

输入：  k（簇的数目），D（包含n个数据的数据集）

输出：  k个簇的集合

算法：

1. 从D中任意选择k个对象作为初始簇中心；
2. repeat
3.   根据cu中对象的均值，把每个对象分配到最相似的簇；
4.   更新簇的均值，即重新计算每个簇中对象的均值；
5. until 簇均值不再发生变化

不能保证k-均值方法收敛于全局最优解，但它常常终止于局部最优解，该算法的结果可能依赖于初始簇中心的随机选择。

k-均值方法不适用于非凸形的簇，或者大小差别很大的簇，此外，它对离群点敏感，因为少量的离群点能够对均值产生极大的影响，影响其他簇的分配。

R语言中，stats包中的kmeans()函数用于实现k-均值聚类分析：

kmeans(x, centers, iter.max = 10, nstart = 1,
       algorithm = c("Hartigan-Wong", "Lloyd", "Forgy","MacQueen"), trace=FALSE)

参数注释：

• x：数值型的向量或矩阵
• centers：簇的数量
• iter.max：重复的最大数量，默认值是10
• nstart：随机数据集的数量，默认值是1
• algorithm：算法的选择，默认值是Hartigan-Wong

函数返回的值：

• cluster ：整数向量，整数值是从1到k，表示簇的编号
• centers：每个簇的中心，按照簇的编号排列
• size：每个簇包含的点的数量

二，k-中心点

k-中心点不使用簇内对象的均值作为参照点，而是挑选实际的数据对象p来代表簇，其余的每个对象被分配到与其最为相似的对象代表p所在的簇中。通常情况下，使用围绕中心点划分（Partitioning Around Medoids，PAM）算法实现k-中心点聚类。

PAM算法的实现过程：

输入：  k（簇的数目），D（包含n个数据的数据集）

输出：  k个簇的集合

算法：

• 从D中随机选择k个对象作为初始的代表对象或种子；
• repeat
•   把每个剩余的对象分配到最近的代表对象p所在的簇；
•   随机地选择一个非代表对象R
•   计算用R代替代表对象p的总代价S；
•   if S<0 then 使用R代替p，形成新的k个代表对象的集合；
• until  代表对象不再变化

当存在离群点时，k-中心点方法比k-均值法更鲁棒。（所谓“鲁棒性”，是指控制系统在一定（结构，大小）的参数摄动下，维持某些性能的特性。），这是因为中心点不像均值法那样容易受到离群点或其他极端值的影响。但是，当n和k的值较大时，k-中心点计算的开销变得相当大，远高于k-均值法。

三，聚类评估

当我们再数据集上试用一种聚类方法时，如何评估聚类的结果的好坏？一般来说，聚类评估主要包括以下任务：

• 估计聚类趋势：仅当数据中存在非随机数据时，聚类分析才是有意义的，因此，评估数据集是否存在随机数据。
• 确定数据集中的簇数：在使用聚类算法之前，需要估计簇数
• 测定聚类质量：在数据集上使用聚类方法之后，需要评估簇的质量。

1，估计聚类趋势

聚类要求数据是非均匀分布的，霍普金斯统计量是一种空间统计量，用于检验空间分布的变量的空间随机性。

comato包中有一个Hopkins.index()函数，用于计算霍普金斯指数，如果数据分布是均匀的，则该值接近于0.5，如果数据分布是高度倾斜的，则该值接近于1。

library(comato)
Hopkins.index(data)

要使用Hopkins.index()评估数据的空间随机性，需要对数据进行无量纲化处理。

2，确定簇数

一个简单的经验方法是：对于n个点的数据集，设置簇数k大约为sqrt(n/2)，在期望情况下，每个簇大约有sqrt(2n)个点。

复杂一点的方法是肘方法（elbow），基于以下观察：增加簇数有助于降低每个簇的簇内方差之和。

给定k>0，计算簇内方差和var(k)，绘制var关于k的曲线，曲线的第一个（或最显著的）拐点暗示正确的簇数。

sjPlot包中sjc.elbow()函数实现了肘方法，可以用于确定k-均值聚类的簇的数目：

library(sjPlot)
sjc.elbow(data, steps = 15, show.diff = FALSE)

参数注释：

• steps：最大的肘值的数量
• show.diff：默认值是FALSE，额外绘制一个图，连接每个肘值，用于显示各个肘值之间的差异，改图有助于识别“肘部”，暗示“正确的”簇数。

sjc.elbow()函数用于绘制k-均值聚类分析的肘值，该函数在指定的数据框计算k-均值聚类分析，产生两个图形：一个图形具有不同的肘值，另一个图形是连接y轴上的每个“步”，即在相邻的肘值之间绘制连线，第二个图中曲线的拐点可能暗示“正确的”簇数。

绘制k均值聚类分析的肘部值。 该函数计算所提供的数据帧上的k均值聚类分析，并产生两个图：一个具有不同的肘值，另一个图绘制在y轴上的每个“步”（即在肘值之间）之间的差异。 第二个图的增加可能表明肘部标准。

library(effects)
library(sjPlot)
library(ggplot2)

sjc.elbow(mtcars,show.diff = FALSE)

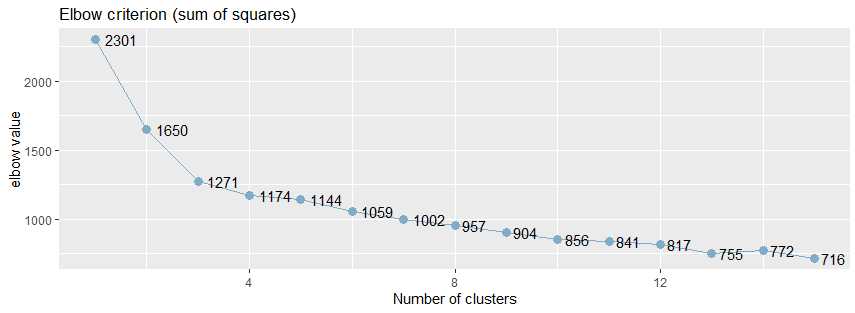
从肘值图中，可以看到曲线的拐点是3，还可以使用NbClust包种的NbClust()函数，该函数提供了26个不同的指标来帮助确定簇的最终数目。

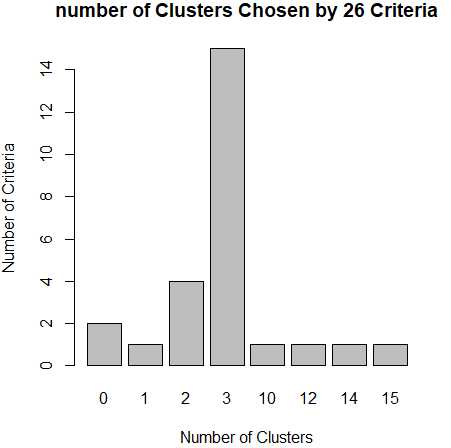
library(NbClust)

nc <- NbClust(df,min.nc = 2,max.nc = 15,method = "kmeans")
barplot(table(nc$Best.nc[1,]),xlab="Number of Clusters",ylab="Number of Criteria",main="number of Clusters Chosen by 26 Criteria")

从条形图种，可以看到支持簇数为3的指标（Criteria）的数量是最多的，因此，基本上可以确定，k-均值聚类的簇数目是3。

3，测定聚类质量

如何比较不同聚类算法产生的聚类？一般而言，根据是否有基准可用，把测定聚类质量的方法分为两类：外在方法和内在方法。

基准是一种理想的聚类，通常由专家构建。如果有可用的基准，那么可以把聚类和基准进行比较，这种方法叫做外在方法。如果没有基准可用，那么通过考虑簇的分离情况来评估簇的好坏，这种方法叫做内在方法。

（1）外在方法

当有基准可用时，使用BCubed 精度（precision）和召回率（recall）来评估聚类的质量。

BCubed根据基准，对给定数据集上聚类中每个对象评估精度（precision）和召回率（recall）。一个对象的精度是指同一簇中有多少个其他对象与该对象同属于一个类别；一个对象的召回率反映有多少同一类别的对象被分配到相同的簇中。

（2）内在方法

当没有数据集的基准可用时，必须使用内在方法来评估聚类的质量。一般而言，内在方法通过考察簇的分离情况和簇的紧凑情况来评估聚类，通常的内在方法都使用数据集的对象之间的相似性度量来实现。

轮廓系数（silhouette coefficient）就是这种相似性度量，轮廓系数的值在-1和1之间，该值越接近于1，簇越紧凑，聚类越好。当轮廓系数接近1时，簇内紧凑，并远离其他簇。

如果轮廓系数sil 接近1，则说明样本聚类合理；如果轮廓系数sil 接近-1，则说明样本i更应该分类到另外的簇；如果轮廓系数sil 近似为0，则说明样本i在两个簇的边界上。所有样本的轮廓系数 sil的均值称为聚类结果的轮廓系数，是该聚类是否合理、有效的度量。

包fpc中实现了计算聚类后的一些评价指标，其中就包括了轮廓系数：avg.silwidth（平均的轮廓宽度）

library(fpc)
result <- kmeans(data,k)
stats <- cluster.stats(dist(data)^2, result$cluster)
sli <- stats$avg.silwidth

包cluster中也包括计算轮廓系数的函数silhouette()：

library (cluster)
library (vegan)

#pam
dis <- vegdist(data)
res <- pam(dis,3) 
sil <- silhouette (res$clustering,dis)

#kmeans
dis <- dist(data)^2
res <- kmeans(data,3)
sil <- silhouette (res$cluster, dis)

四，k-均值聚类分析实践

有效的聚类分析是一个多步骤的过程，其中每一次决策都可能影响聚类结果的质量和有效性，我们使用k-均值聚类来处理葡萄酒中13种化学成分的数据集wine，这个数据集可以通过rattle包获得，

install.packages("rattle")
data(wine,package="rattle")
head(wine)

  Type Alcohol Malic  Ash Alcalinity Magnesium Phenols Flavanoids Nonflavanoids Proanthocyanins Color  Hue Dilution Proline
1    1   14.23  1.71 2.43       15.6       127    2.80       3.06          0.28            2.29  5.64 1.04     3.92    1065
2    1   13.20  1.78 2.14       11.2       100    2.65       2.76          0.26            1.28  4.38 1.05     3.40    1050
3    1   13.16  2.36 2.67       18.6       101    2.80       3.24          0.30            2.81  5.68 1.03     3.17    1185
4    1   14.37  1.95 2.50       16.8       113    3.85       3.49          0.24            2.18  7.80 0.86     3.45    1480
5    1   13.24  2.59 2.87       21.0       118    2.80       2.69          0.39            1.82  4.32 1.04     2.93     735
6    1   14.20  1.76 2.45       15.2       112    3.27       3.39          0.34            1.97  6.75 1.05     2.85    1450

1，选择合适的变量

第一个变量Type是类型，可以忽略,其他13个变量是葡萄酒的13总化学成分，选择这13个变量进行聚类分析。由于变量值变化很大，所以需要在聚类之前对其进行标准化处理。

2，标准化数据

使用scale()函数对数据进行无量纲化处理，

df <- scale(wine[,-1])

3，评估聚类的趋势

变量df的变量值是无量纲的，可以直接使用函数Hopkins.index()计算数据的空间分布的随机性，得出的结果越接近于1，说明数据的空间分布高度倾斜，空间随机性越高。

install.packages("comato")
library(comato)
Hopkins.index(df)

[1] 0.7412846

4，确定聚类的簇数

使用sjPlot包中的sjc.elbow()函数计算肘值，曲线的拐点出现3左右，这说明，使用k-均值法进行聚类分析时，可以设置的簇数大概是3。

install.packages("effects")
install.packages("sjplot")

library(effects)
library(sjPlot)
library(ggplot2)

sjc.elbow(df,show.diff = FALSE)

 

从肘值图中，可以看到曲线的拐点是3，还可以使用NbClust包种的NbClust()函数，该函数提供了26个不同的指标来帮助确定簇的最终数目。

install.packages("NbClust")
library(NbClust)

nc <- NbClust(df,min.nc = 2,max.nc = 15,method = "kmeans")
barplot(table(nc$Best.nc[1,]),xlab="Number of Clusters",ylab="Number of Criteria",main="number of Clusters Chosen by 26 Criteria")

从条形图种，可以看到支持簇数为3的指标（Criteria）的数量是最多的，因此，基本上可以确定，k-均值聚类的簇数目是3。

5，测定聚类的质量

使用轮廓系数测定聚类的质量，轮廓系数的值在-1和1之间，该值越接近于1，簇越紧凑，聚类越好。当轮廓系数接近1时，簇内紧凑，并远离其他簇。

install.packages("fpc")

library(fpc)
for(k in 2:9){
result <- kmeans(df,k)
stats <- cluster.stats(dist(df)^2, result$cluster)
sli <- stats$avg.silwidth

print(paste0(k,‘-‘,sli))
}

当簇数目为3时，聚类的轮廓系数0.45是最好的。

[1] "2-0.425791262898175"
[1] "3-0.450837233419168"
[1] "4-0.35109709657011"
[1] "5-0.378169006474844"
[1] "6-0.292436629924875"
[1] "7-0.317163857046711"
[1] "8-0.229405778112672"
[1] "9-0.291438101137107"

 

参考文档：

聚类簇数制定_肘方法elbow

霍普金斯统计量(Hopkins)判断数据集是否是均匀分布_聚类

确定最佳聚类数目的10种方法