杂题总汇HDU多校赛第十场 Videos

Posted 2020-12-31 luckyglass-blog

【HDU2018多校赛第十场】Videos

最后一场比赛也结束了……

+HDU传送门+

---

 

◇ 题目

<简要翻译>

有n个人以及m部电影，每个人都有一个快乐值。每场电影都有它的开始、结束时间和看了这部电影会得到的快乐值。电影分成两种类型，若同一个人连续（不是时间连续，是顺序连续）看了两部相同类型的电影，他的快乐值会扣除W，数据保证扣除的值不超过电影增加的快乐值。

特别的，一个人换电影不花费时间，即若第一部电影的结束时间等于下一部电影的开始时间，是可以两场都看的；看电影必须看完；一部电影只能一个人看。

<输入&输出>

输入包含多组数据，第一行为整数T表示数据组数。

每组数据第一行包含四个整数t,m,n,W，t表示电影结束的最晚时间不超过t，m表示电影的数量，n表示人的数量，W表示连续看相同类型的电影扣除的快乐值；接下来m行，每行描述一个电影，包含四个整数——s[i]、e[i]表示第i部电影的开始和结束时间，w[i]表示看第i部电影得到的快乐值，k[i]表示电影的类型，为0或1。

输出所有人的快乐值之和的最大值。

<样例&解释>

Input	Output	Explain
2 10 3 1 10 1 5 1000 0 5 10 1000 1 3 9 10 0 10 3 1 10 1 5 1000 0 5 10 1000 0 3 9 10 0	2000 1990	第一组数据只有一个人，依次看了 第1,2部电影； 第二组数据只有一个人，依次看了 第1,2部电影，但类型相同，扣除 10；

 

 

 

 

 

 

 

 

 

 

 

---

 

 

◇ 解析

这道题是一道网络流的题……其中网络流的部分是队友不知道哪里找来的版，就不解释了QwQ

由于网络流的最大流无法处理多个人的情况，我们使用费用流，那么思路就非常清晰了——网络流中“流”的是人的个数，而费用就是每部电影的快乐值；

也就是说我们要求一个最大费用费用流，其实可以将所有边的费用取相反数，然后跑最小费用就可以了??

唯一难的就是建图。下面就直接列出建图方法了：

① 总共有n个人，为了避免一个人同时看了两部电影，我们先建立n个点每个点表示一个人，连接超级源点，容量为1（一个人），费用为0；

② 总共m部电影，一个人可以从任何一个电影开始看，所以建立m个节点，将每一部电影都跟所有的人连接，容量为1，费用为电影的快乐值（走过这条边就会增加快乐值，相当于看了这部电影，且限制了看电影的人数）；

③ 若第i部电影的结束时间小于等于第j部电影的结束时间，则在第i部电影和第j部电影之间连边，容量依然为1，费用为第j部电影的快乐值，若电影i,j的类型相同，边的费用减去W（看完第i部电影再看第j部）；

④ 由于一个人可以看完一部电影就不看了，即可以从任何一部电影结束，所以将所有电影与超级汇点连边；没有必要在人与汇点连边，因为看一部电影始终优于不看，则限制每个人都要看电影。

但是交上去就WA了，后面一个dalao来检查了一下~发现了一个BUG：

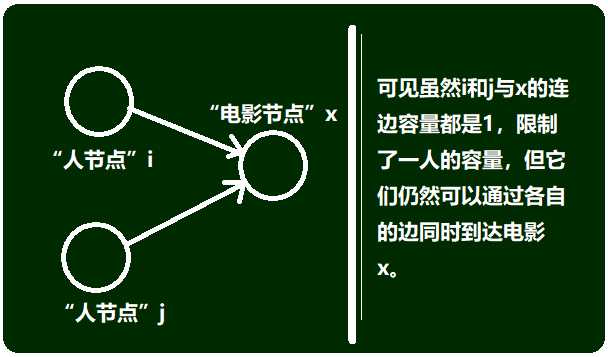
虽然有边的容量限制人数，但是下面这种情况会出现两个人看了同一部电影：

如何解决这种问题？

根据以前做题的经验（好吧，其实是dalao直接告诉我们的）我们需要拆点——将每一个电影节点拆分出一个虚拟节点，真节点与虚拟节点之间连一条容量为1，花费为0的边，所有以电影i为末尾的边都连在真节点上，而以电影i出发的边都连在虚拟节点上——只要经过电影i，则必然要通过真节点和虚拟节点的边，这样就限制了一个人通过。

虽然话是这么说，但是实际上建边时，边的花费我都取了相反数，这样就能够用跑最小费用流代替最大费用流，有负权边，注意选择合适的方法。

---

 

◇ 源代码（其中最小费用流的部分是从不知道哪个dalao那里copy过来的……真是非常感谢！！）

/*Lucky_Glass*/ 
#include<cstdio>
#include<cstring>
#include<queue>
#include<iostream>
#include<algorithm>
using namespace std;
/*以下均是模板*/
const int N = 50002;
const int M = 500005;
#define INF 0x3f3f3f3f
struct E
{
    int to,cap,cost,flow,next;
}e[2*M];int head[N] , ecnt;
int  pre[N];
int dis[N];
bool vis[N];
int n,m,S,T;

void Clear()
{
    ecnt = 0;
    memset(head,-1,sizeof head);
}

void adde(int fr,int to,int cap,int cost)
{
    e[ecnt]=(E){to,cap,-cost,0,head[fr]};
    head[fr] = ecnt++;
    e[ecnt]=(E){fr,0,cost,0,head[to]};
    head[to] = ecnt++;
}

bool SPFA(int s,int t)
{
    memset(vis,0,sizeof vis);
    memset(dis,0x3f,sizeof dis);
    memset(pre,-1,sizeof pre);
    queue <int> q;
    q.push(s);dis[s] = 0;vis[s]=1;

    while (!q.empty())
    {
        int cur = q.front();q.pop();vis[cur] = false;
        for (int j=head[cur];j!=-1;j=e[j].next)
        {
            int to = e[j].to;
            if (dis[to] > dis[cur] + e[j].cost && e[j].cap > e[j].flow )
            {
                dis[to] = dis[cur] + e[j].cost;
                pre[to] = j;
                if (!vis[to])
                {
                    q.push(to);
                    vis[to] = true;
                }
            }
        }
    }
    return pre[t] != -1;
}

void MCMF (int s,int t,int &maxflow,int &mincost)
{
    maxflow = mincost = 0;
    while (SPFA(s,t))
    {
        int MIN = INF;
        for (int j=pre[t]; j!=-1;j=pre[e[j^1].to])
        {
            MIN = min(MIN,e[j].cap - e[j].flow);
        }
        for (int j=pre[t]; j!=-1;j=pre[e[j^1].to])
        {
            e[j].flow += MIN;
            e[j^1].flow -= MIN;
            mincost += MIN * e[j].cost;
        }
        maxflow += MIN;
    }
}
/*模板结束*/
#define MAXN 3000

int L[MAXN+5],R[MAXN+5],Lk[MAXN+5],Kd[MAXN+5];
int main(){
    int TT;
    cin>>TT;//数据组数 
    while(TT--){
        Clear();//清空 
        int nn,mm,kk,ht;
        cin>>nn>>mm>>kk>>ht;
        for(int i=1;i<=mm;i++)
            cin>>L[i]>>R[i]>>Lk[i]>>Kd[i];
        S=1,T=kk+mm*2+2;
//超级源点为1，超级汇点为最后一个点（因为有kk个人节点，mm*2个电影节点，即真节点和虚拟节点，再加上一个源点） 
        for(int i=1;i<=kk;i++)
            adde(S,i+1,1,0); //在人节点和源点之间连边，第i个人编号为i+1 
        for(int i=1;i<=kk;i++)
            for(int j=1;j<=mm;j++)
                adde(i+1,j+kk+1,1,Lk[j]); //在人和电影的真节点之间连边，第i部电影真节点编号为i+kk+1 
        for(int i=1;i<=mm;i++)
            adde(i+kk+1,i+kk+mm+1,1,0); //连接真节点和虚拟节点，第i部电影的虚拟节点编号为i+kk+mm+1 
        for(int i=1;i<=mm;i++)
            adde(i+kk+mm+1,T,1,0); //连接虚拟节点和汇点 
        for(int i=1;i<=mm;i++)
            for(int j=1;j<=mm;j++)
                if(i!=j&&R[i]<=L[j]){ //电影之间连边，虚拟节点连真节点 
                    if(Kd[i]!=Kd[j])
                        adde(i+kk+mm+1,j+kk+1,1,Lk[j]);
                    else
                        adde(i+kk+mm+1,j+kk+1,1,Lk[j]-ht);
                }
        int ans1,ans2;
        MCMF(S,T,ans1,ans2);
        cout<<-ans2<<"
"; //由于边权取了相反数，输出答案时也需要取相反数 
    }
}

　　

---

 

The End

Thanks for reading!

- Lucky_Glass

（Tab：如果我有没讲清楚的地方可以直接在邮箱[email protected] email我，在周末我会尽量解答并完善博客~??）