用二项逻辑斯蒂回归解决二分类问题

Posted 2020-12-31 softwarebuilding

逻辑斯蒂回归:

逻辑斯蒂回归是统计学习中的经典分类方法，属于对数线性模型。logistic回归的因变量可以是二分类的，

也可以是多分类的

基本原理

logistic 分布

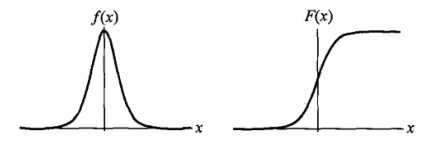
折X是连续的随机变量，X服从logistic分布是指X具有下列分布函数和密度函数:

 

其中为位置参数，为形状参数。与图像如下，其中分布函数是以为中心对阵，越小曲线变化越快

 

二项logistic回归模型；

二项logistic回归模型如下:

 

其中是输入，输出，W称为权值向量，b称为偏置， 是w和x的内积

 

参数估计

 

? 假设：

 

?

 

  

 

? 则似然函数为:

 

?

 

  

 

? 求对数似然函数：

 

?

 

  

 

?

 

  

 

? 从而对

 

  

 

求极大值，得到w的估计值。求极值的方法可以是梯度下降法，梯度上升法等。

 

示例代码: 

#导入需要的包：

from pyspark import SparkContext

from pyspark.sql import SparkSession,Row,functions

from pyspark.ml.linalg import Vector,Vectors

from pyspark.ml.evaluation import MulticlassClassificationEvaluator

from pyspark.ml import Pipeline

from pyspark.ml.feature import IndexToString,StringIndexer,VectorIndexer,HashingTF,Tokenizer

from pyspark.ml.classification import LogisticRegression,LogisticRegressionModel,BinaryLogisticRegressionSummary,LogisticRegression

#用二项逻辑斯蒂回归解决 二分类 问题

 

sc = SparkContext(‘local‘,‘用二项逻辑斯蒂回归解决二分类问题‘)

spark = SparkSession.builder.master(‘local‘).appName(‘用二项逻辑斯蒂回归解决二分类问题‘).getOrCreate()

 

#读取数据，简要分析

#我们定制一个函数，来返回一个指定的数据，然后读取文本文件，第一个map把每行的数据用","

#隔开，比如在我们的数据集中，每行被分成了5部分，目前4部分是鸢尾花的四个特征，最后一部分鸢尾花的分类；

#我们这里把特征存储在Vector中，创建一个Iris模式的RDd，然后转化成DataFrame;最后调用show()方法查看数据

def f(x):

rel ={}

rel[‘features‘] = Vectors.dense(float(x[0]),float(x[1]),float(x[2]),float(x[3]))

rel[‘label‘] = str(x[4])

return rel

data= sc.textFile("file:///usr/local/spark/mycode/exercise/iris.txt").map(lambda line : line.split(‘,‘)).map(lambda p : Row(**f(p))).toDF()

# 因为我们现在处理的是2分类问题，所以我们不需要全部的3类数据，我们要从中选出两类的

#数据。这里首先把刚刚得到的数据注册成一个表iris，注册成这个表之后，我们就可以

#通过sql语句进行数据查询，比如我们这里选出了所有不属于“Iris-setosa”类别的数

#据；选出我们需要的数据后，我们可以把结果打印出来看一下，这时就已经没有“Iris-setosa”类别的数据

data.createOrReplaceTempView("iris")

df = spark.sql("select * from iris where label != ‘Iris-setosa‘")

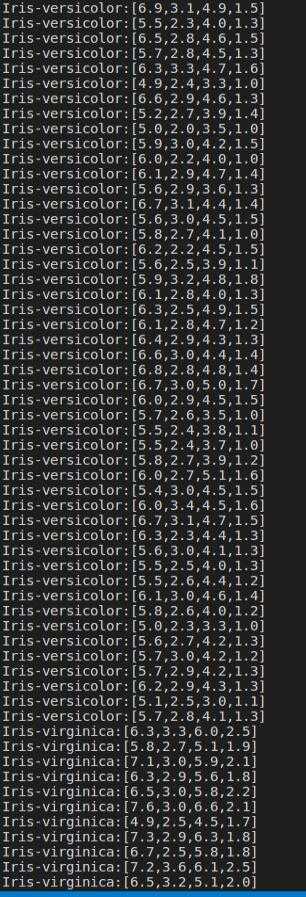
rel = df.rdd.map(lambda t : str(t[1])+":"+str(t[0])).collect()

for item in rel:

print(item)

如图:

　　

 

#构建ML的pipeline

#分别获取标签列和特征列，进行索引，并进行了重命名

labelIndexer = StringIndexer().setInputCol(‘label‘).setOutputCol(‘indexedLabel‘).fit(df)

featureIndexer = VectorIndexer().setInputCol(‘features‘).setOutputCol(‘indexedFeatures‘).fit(df)

#把数据集随机分成训练集和测试集，其中训练集占70%

trainingData, testData =df.randomSplit([0.7,0.3])

#设置logistic的参数，这里我们统一用setter的方法来设置，也可以用ParamMap来设置

#（具体的可以查看spark mllib的官网）。这里我们设置了循环次数为10次，正则化项为

#0.3等，具体的可以设置的参数可以通过explainParams()来获取，还能看到我们已经设置

#的参数的结果。

lr= LogisticRegression().setLabelCol("indexedLabel").setFeaturesCol(‘indexedFeatures‘).setMaxIter(10).setRegParam(0.3).setElasticNetParam(0.8)

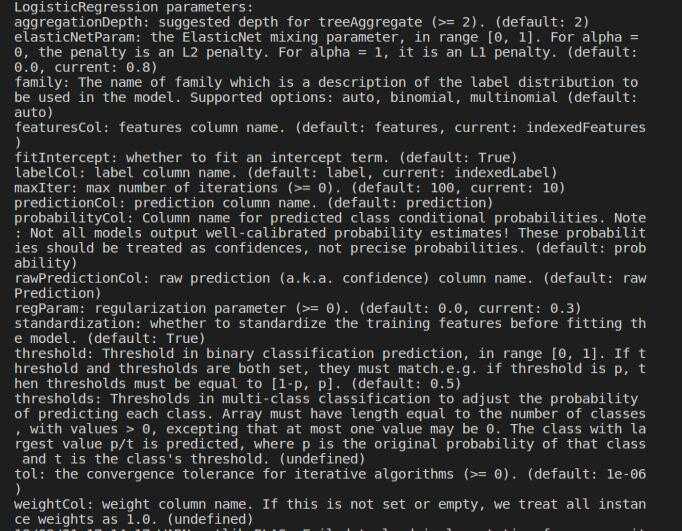
print("LogisticRegression parameters: "+ lr.explainParams())

如图:

 

#设置一个labelConverter，目的是把预测的类别重新转化成字符型的

labelConverter = IndexToString().setInputCol("prediction").setOutputCol("predictedLabel").setLabels(labelIndexer.labels)

#构建pipeline，设置stage，然后调用fit()来训练模型

LrPipeline = Pipeline().setStages([labelIndexer, featureIndexer, lr, labelConverter])

LrPipelineModel = LrPipeline.fit(trainingData)

#用训练得到的模型进行预测，即对测试数据集进行验证

lrPredictions = LrPipelineModel.transform(testData)

preRel = lrPredictions.select("predictedLabel",‘label‘,‘features‘,‘probability‘).collect()

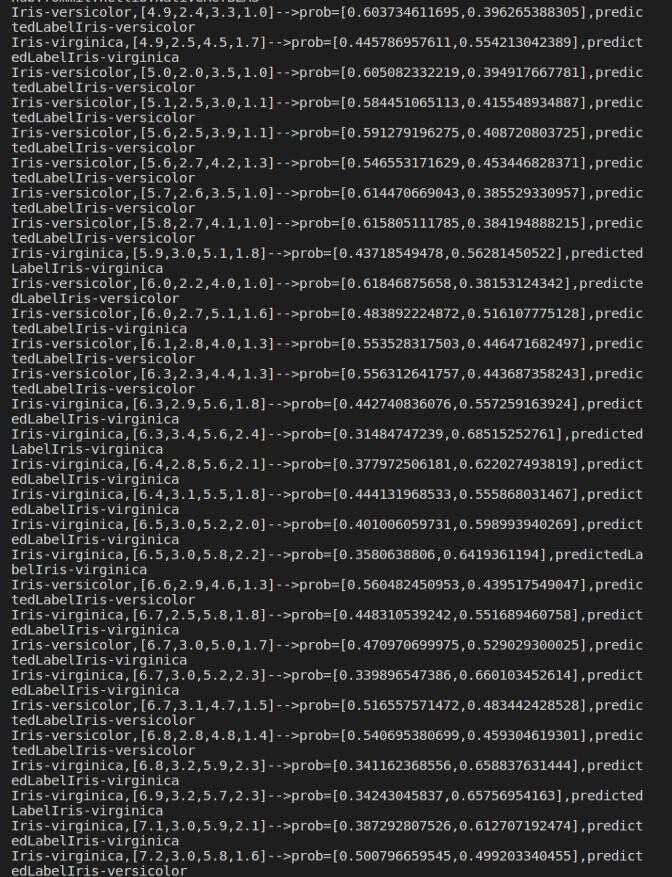
for item in preRel:

print(str(item[‘label‘])+‘,‘+str(item[‘features‘])+‘-->prob=‘+str(item[‘probability‘])+‘,predictedLabel‘+str(item[‘predictedLabel‘]))

如图:

 

#模型评估1

#创建一个MulticlassClassificationEvaluator实例，用setter方法把预测分类的列名和真实分类的列名进行设置；然后计算预测准确率和错误率

evaluator = MulticlassClassificationEvaluator().setLabelCol("indexedLabel").setPredictionCol("prediction")

lrAccuracy = evaluator.evaluate(lrPredictions)

print("Test Error=" + str(1.0- lrAccuracy))

如图:

 

#从上面可以看到预测的准确性达到94%，接下来我们可以通过model来获取我们训练得到

#的逻辑斯蒂模型。前面已经说过model是一个PipelineModel，因此我们可以通过调用它的

#stages来获取模型

lrModel = LrPipelineModel.stages[2]

print("Coefficients: " + str(lrModel.coefficients)+"Intercept: "+str(lrModel.intercept)+"numClasses: "+str(lrModel.numClasses)+"numFeatures: "+str(lrModel.numFeatures))

如图:

 

 

#模型评估2

#spark的ml库还提供了一个对模型的摘要总结（summary），不过目前只支持二项逻辑斯

#蒂回归，而且要显示转化成BinaryLogisticRegressionSummary 。在下面的代码中，首

#先获得二项逻辑斯模型的摘要；然后获得10次循环中损失函数的变化，并将结果打印出来

#，可以看到损失函数随着循环是逐渐变小的，损失函数越小，模型就越好；接下来，我们

#把摘要强制转化为BinaryLogisticRegressionSummary，来获取用来评估模型性能的矩阵；

#通过获取ROC，我们可以判断模型的好坏，areaUnderROC达到了 0.969551282051282，说明

#我们的分类器还是不错的；最后，我们通过最大化fMeasure来选取最合适的阈值，其中fMeasure

#是一个综合了召回率和准确率的指标，通过最大化fMeasure，我们可以选取到用来分类的最合适的阈值

trainingSummary = lrModel.summary

objectiveHistory = trainingSummary.objectiveHistory

for item in objectiveHistory:

print (item)

print("areaUnderRoC:"+str(trainingSummary.areaUnderROC))

如图:

 

 

fMeasure = trainingSummary.fMeasureByThreshold

maxFMeasure = fMeasure.groupBy().max(‘F-Measure‘).select(‘max(F-Measure)‘).head()

print(maxFMeasure)

如图:

 

bestThreshold = fMeasure.where(fMeasure[‘F-Measure‘] == maxFMeasure[‘max(F-Measure)‘]).select(‘threshold‘).head()[‘threshold‘]

print(bestThreshold)

lr.setThreshold(bestThreshold)

#用多项逻辑斯蒂回归解决 二分类 问题

mlr = LogisticRegression().setLabelCol("indexedLabel").setFeaturesCol("indexedFeatures").setMaxIter(10).setRegParam(0.3).setElasticNetParam(0.8).setFamily("multinomial")

mlrPipeline = Pipeline().setStages([labelIndexer, featureIndexer, mlr, labelConverter])

mlrPipelineModel = mlrPipeline.fit(trainingData)

mlrPrediction = mlrPipelineModel.transform(testData)

mlrPreRel =mlrPrediction.select("predictedLabel", "label", "features", "probability").collect()

for item in mlrPreRel:

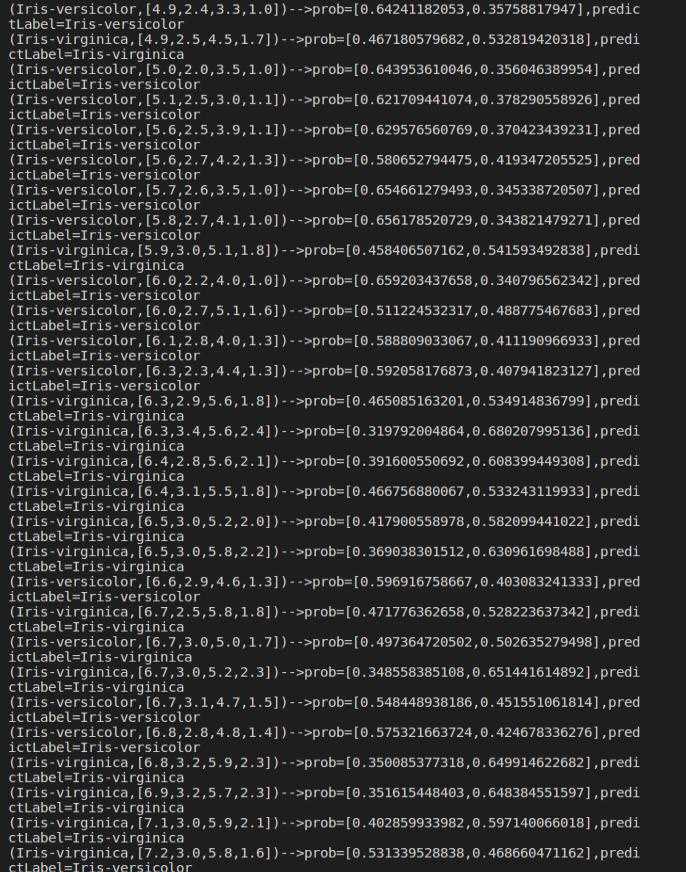
print(‘(‘+str(item[‘label‘])+‘,‘+str(item[‘features‘])+‘)-->prob=‘+str(item[‘probability‘])+‘,predictLabel=‘+str(item[‘predictedLabel‘]))

如图:

 

mlrAccuracy = evaluator.evaluate(mlrPrediction)

print("mlr Test Error ="+ str(1.0-mlrAccuracy))

如图:

mlrModel = mlrPipelineModel.stages[2]

print("Multinomial coefficients: " +str(mlrModel.coefficientMatrix)+"Multinomial intercepts: "+str(mlrModel.interceptVector)+"numClasses: "+str(mlrModel.numClasses)+"numFeatures: "+str(mlrModel.numFeatures))

如图；

#用多项逻辑斯蒂回归解决多分类问题

mlrPreRel2 = mlrPrediction.select("predictedLabel", "label", "features", "probability").collect()

for item in mlrPreRel2:

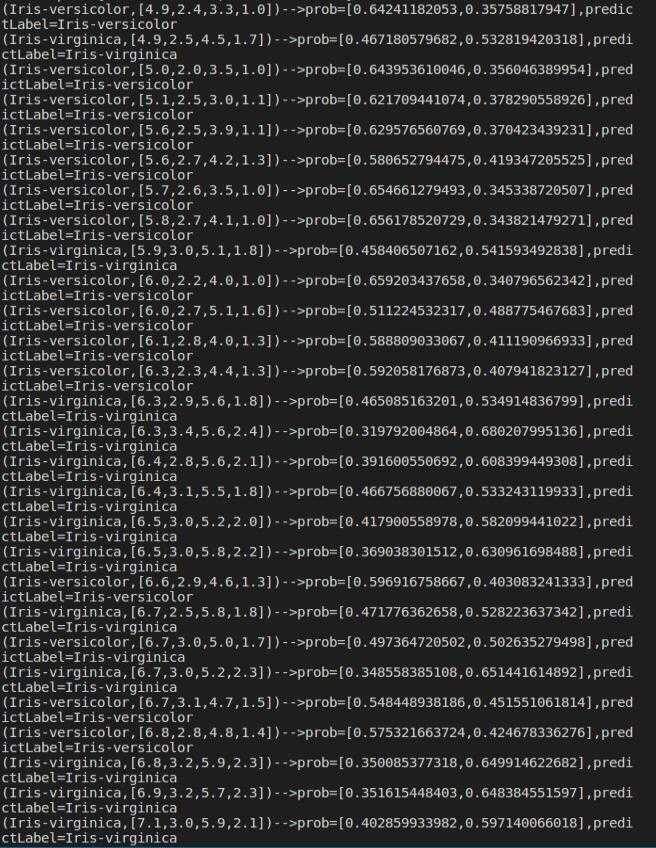
print(‘(‘+str(item[‘label‘])+‘,‘+str(item[‘features‘])+‘)-->prob=‘+str(item[‘probability‘])+‘,predictLabel=‘+str(item[‘predictedLabel‘]))

如图:

 

mlr2Accuracy = evaluator.evaluate(mlrPrediction)

print("Test Error = " + str(1.0 - mlr2Accuracy))

 

mlr2Model = mlrPipelineModel.stages[2]

print("Multinomial coefficients: " + str(mlrModel.coefficientMatrix)+"Multinomial intercepts: "+str(mlrModel.interceptVector)+"numClasses: "+str(mlrModel.numClasses)+"numFeatures: "+str(mlrModel.numFeatures))