『8.21 模拟赛』冒泡排序 II

Posted 2020-12-31 fang-hao

题目描述

前一天的冒泡排序对rsw来说太简单了，所以又有了冒泡排序2，给定n,k,q，问：有多少个不同的1~n的排列，能够使得，冒泡排序k趟后，得到一个几乎正确的序列。

一个几乎正确的序列指的是：它的最长上升子序列的长度至少是n-1。

解题思路

思路就是没有思路。。。。

昨天刚刚做过一道冒泡排序的题，有一个结论在这里

每个位置上的数最远是由前面的第k个位置转移过来的，并且题目中要求最长上升子序列最短是n-1的长度，所以只有两种情况:

1） 最终是从小到大排序好的

2）最终是从小到大排序好的序列中选择一段向前循环滚动一个位置或者向后滚动一个位置，这样就有一个数在它不应该在的位置

我们既然正着推不好推，那我们就反着推呗，从每个几乎正确的序列转移到最初的情况。

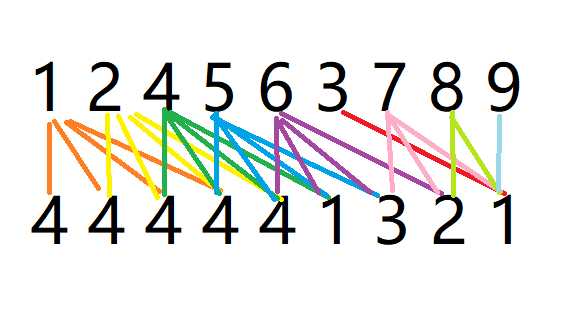
比如这张图片，k=3。3，4，5，6向前滚动了一次，下面代表着每个位置的数的位置有集中选择，显然，在3前面，每个数都有k+1种选择，然鹅到了3，我们只能把它放在9那里，为什么呢？ 如果3在8上，那排完序后3一定跑到6哪里去了，对吧？剩下的数，由于区间长度不过了，他们只能找位置放在最后的地方了，所以是3，2，1。

那么，除了3和最后k个没地方往后放的数以外，所有数都有k+1种放的方法，所以我们先有((k+1)^left(n-k-1 ight))种放的方法，后面的几个数没地方放了，那答案就是(k!)，由乘法原理可以得到这样的答案总数为((k+1)^left(n-k-1 ight)×k!)。假设区间长为i，这样下来，总共有n-k-i+1个地方可以选做区间的开头，所以总答案就是((k+1)^left(n-k-1 ight)×k!×(n-k-i+1))。

向右平移的方法跟这个差不多，按照这个方法也可以推出来。

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define ll long long
using namespace std;
ll p[100];
ll n,k,q;
int main(){
    scanf("%lld%lld%lld",&n,&k,&q);
    p[0]=1;
    for(register ll i=1;i<100;i++)p[i]=(p[i-1]*(k+1))%q;
    k=min(k,n);
    ll ans=p[n-k];
    for(register ll i=2;i+k<=n;i++){
        ans=(ans+(ll)(n-k+1-i)*(ll)p[n-k+1-i])%q;
    }
    for(register ll i=3;i+k<=n;i++){
        ans=(ans+(ll)(n-k+1-i)*(ll)p[n-k-1])%q;
    }
    for(register ll i=1;i<=k;i++){
        ans=(ans*i)%q;
    }
    cout<<ans<<endl;
}