8.21总结前日及今日
Posted romalzhih
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了8.21总结前日及今日相关的知识,希望对你有一定的参考价值。
估计拿不到打区域赛的名额了,还是有点忧伤,哎
A题:
题意:
给出一个0~n-1的单词表,问要组成一个长度为m,且单词权值之和为k的单词,的方案总数有多少种
解法:
其实就是问把k个球放到m个桶中(同中球数可以为空),且每个桶中的球数不超过n-1个,的方案总数。(仔细想一下,很有意思)
怎么容斥? 总情况数 — 桶中球数超过n个的情况数即可,即:
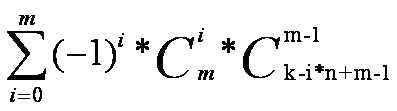
当i等于0的时候,即是总的方案数,注意容斥的时候是奇数项为负,偶数项为正
1 #include<cstdio> 2 #include<cmath> 3 using namespace std; 4 const int maxn = 1e6 + 7; 5 const long long mod = 998244353; 6 long long fac[maxn], inv[maxn]; 7 long long tmp[maxn]; 8 int n, m, k; 9 int t; 10 11 void init() 12 { 13 tmp[0] = tmp[1] = 1; 14 inv[1] = inv[0] = 1; 15 for (int i = 2; i < maxn; i++) 16 { 17 tmp[i] = (mod - mod / i) * tmp[mod % i] % mod; 18 inv[i] = inv[i - 1] * tmp[i] % mod; 19 } 20 fac[0] = 1; 21 for (int i = 1; i < maxn; i++) 22 fac[i] = (fac[i - 1] * i) % mod; 23 } 24 25 long long c(int n, int m) //c(n,m) 26 { 27 if (n < m) return 0; 28 return fac[n] % mod * inv[n - m] % mod * inv[m] % mod; 29 } 30 31 long long solve(int i) 32 { 33 return c(m + k - 1 - i * n, m - 1) % mod * c(m, i) % mod; 34 } 35 36 int main(int argc, char const *argv[]) 37 { 38 init(); 39 scanf("%d", &t); 40 while (t--) 41 { 42 scanf("%d%d%d", &n, &m, &k); 43 long long ans = 0; 44 for (int i = 0; i <= m && (i * n) <= k; i++) 45 { 46 if (i % 2) ans -= solve(i); 47 else ans += solve(i); 48 } 49 ans %= mod; 50 printf("%lld ", (ans + mod) % mod); 51 } 52 return 0; 53 }
Uva12034
题意:两匹马比赛有三种比赛结果,n匹马比赛的所有可能结果总数
解法:
设答案是f[n],则假设第一名有i个人,有C(n,i)种可能,接下来还有f(n-i)种可能性,因此答案为 ΣC(n,i)f(n-i)
另外这里给出两个求组合数的模板,卢卡斯定理的p是模数,并且要求是素数,第二个是递推式,适合于n<2000的情况
1 #include<cstdio> 2 using namespace std; 3 const int maxn = 1e3; 4 const int mod = 10056; 5 typedef long long ll; 6 7 /*--------------------------卢卡斯定理取模-----------------------*/ 8 ll exp_mod(ll a, ll b, ll p) { 9 ll res = 1; 10 while (b != 0) { 11 if (b & 1) res = (res * a) % p; 12 a = (a*a) % p; 13 b >>= 1; 14 } 15 return res; 16 } 17 18 ll Comb(ll a, ll b, ll p) { 19 if (a < b) return 0; 20 if (a == b) return 1; 21 if (b > a - b) b = a - b; 22 23 ll ans = 1, ca = 1, cb = 1; 24 for (ll i = 0; i < b; ++i) { 25 ca = (ca * (a - i)) % p; 26 cb = (cb * (b - i)) % p; 27 } 28 ans = (ca*exp_mod(cb, p - 2, p)) % p; 29 return ans; 30 } 31 //Lucas定理对组合数取模 32 ll Lucas(int n, int m, int p) { 33 ll ans = 1; 34 while (n&&m&&ans) { 35 ans = (ans*Comb(n%p, m%p, p)) % p; 36 n /= p; 37 m /= p; 38 } 39 return ans; 40 } 41 42 /*----------------------组合数递推公式(适用n<2000)---------------------------*/ 43 int C[maxn+10][maxn+10]; 44 void Cal_C(int n) { 45 //传递的是一个二维的数组c 46 for (int i = 0; i <= n; i++){ 47 C[i][0] = C[i][i] = 1; 48 for (int j = 1; j < i; j++) 49 C[i][j] = (C[i - 1][j - 1]%mod + C[i - 1][j]%mod)%mod; 50 } 51 return; 52 } 53 /*--------------------------------------------------------------------------*/ 54 55 int f[maxn+11]; 56 void generate() { 57 Cal_C(maxn); 58 f[0] = 1; 59 for (int i = 1; i <= maxn; i++) { 60 f[i] = 0; 61 for (int j = 1; j <= i; j++) 62 f[i] = (f[i] + C[i][j] * f[i - j]) % mod; 63 } 64 return; 65 } 66 67 int main() { 68 int T; scanf("%d", &T); 69 int kase = 1; 70 generate(); 71 while (T--) { 72 int n; scanf("%d", &n); 73 printf("Case %d: %d ", kase++, f[n]); 74 } 75 return 0; 76 }
Uva12230
题意:A,B相距D,A,B间有n条河,河宽Li,每条河上有一个速度为vi的船,在河山来回行驶,每条河离A的距离为pi,现在求从A到B时间的期望,步行速度始终为1
解法:首先如果全部步行则期望为D,现在每遇到一条河,求过河时间的期望,等待时间的区间为(0,2*L/v),船在每个地方都是等可能的,所以等待的期望就是(0 + 2*L/v) / 2 = L / v,又过河还要L / v,所以总的渡河期望值为2 * L / v,所以每遇到一条河拿D减去假设步行过河的期望L再加上实际过河期望2 * L / v即可,最后发现和p没有卵关系,真开心~
1 #include<iostream> 2 using namespace std; 3 4 int main() { 5 int n, dis; 6 int kase = 1; 7 while (scanf("%d%d", &n, &dis)) { 8 if (n == 0 && dis == 0)break; 9 double ans = 0, suml = 0; 10 for (int i = 1; i <= n; i++) { 11 double p, l, v; cin >> p >> l >> v; 12 ans += 2 * l / v; 13 suml += l; 14 } 15 ans += (dis - suml); 16 printf("Case %d: %.3f ", kase++, ans); 17 } 18 return 0; 19 }
Uva1639
题意:
有两个盒子各有n个糖果(n<=200000),每天随机选择一个:选第一个盒子的概率是p(0 ≤ p ≤ 1),第二个盒子的概率为1-p,然后吃掉其中的一颗。直到有一天,随机选择一个盒子打开一看,没糖了!现在请你计算另一个盒子里剩下的糖果数量的期望值。
解法:
我们假设到第n天的时候取得是第1个盒子的糖,此时第2个盒子有i颗糖,则在此之前打开了n+(n-i)次盒子, 其中n次打开了第一个盒子,(n-i)次打开了第二个盒子,则概率是C(2n-i,n)*p^(n+1)*(1-p)^n-i。
由于n高达20w,所以二次项系数会非常大,而后面的概率会非常小,所以如果直接计算会爆精度,所以这里我们用求对数的方法进行计算
1 #include<iostream> 2 #include<cmath> 3 using namespace std; 4 typedef long double lb; 5 const int maxn = 2e5 + 5; 6 long double logF[2 * maxn + 66]; 7 8 void generate() { 9 //预处理出n!的log值 10 logF[0] = 0; 11 for (int i = 1; i <= maxn; i++) 12 logF[i] = logF[i - 1] + log(i); 13 } 14 // C(n,m) = n!/(m!(n-m)!) 15 long double logC(int n, int m) { 16 return logF[n] - logF[m] - logF[n - m]; 17 } 18 19 int main() { 20 int n; double p; 21 generate(); 22 int kase = 1; 23 while (scanf("%d%lf", &n, &p)!=EOF) { 24 double ans = 0; 25 for (int i = 0; i <= n; i++) { 26 long double v1 = logC(2 * n - i, n) + (n + 1)*log(p) + (n - i)*log(1 - p); 27 long double v2 = logC(2 * n - i, n) + (n + 1)*log(1 - p) + (n - i)*log(p); 28 ans += (i*(exp(v1) + exp(v2))); 29 } 30 printf("Case %d: %.6lf ", kase++, ans); 31 } 32 return 0; 33 }
Uva1640
题意:
统计两个整数a,b之间各个数字(0~9)出现的次数,如1024和1032,他们之间的数字有1024 1025 1026 1027 1028 1029 1030 1031 1032 总共有10个0,10个1,3个3等等。
解法:
这类问题的一般步骤都是先用f(n,d)计算出0~n中d数字出现的次数,那么答案就是f(b,d)-f(a-1,d)
下面程序中的注释为(1,2974)的第一层(未递归)解释,递归后同理
1-2974 拆分为1-2970 和 2971-2974
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 using namespace std; 5 int l, r; 6 int a[11], b[11]; 7 8 void solve(int n, int m) { 9 int x = n / 10;//除了末位以外的 x=297 10 int y = n % 10;//最后一位的数字范围 y=4 11 int tmp = x; 12 //计算小于10*x+1到10*x+y中个位数的个数,b[1-y]也就是(2971-2974)个位数 13 for (int i = 1; i <= y; i++)b[i] += m; 14 //计算10*x-10到10*x-1中个位数的总个数,296 0-296 9 个位数个数每个都是296个 15 for (int i = 0; i <= 9; i++)b[i] += m*x; 16 while (tmp) { 17 //10*x 到10*x+y非个位的个数,因为从0开始,所以*(y+1)就是非个位位数,当然还要乘m 18 b[tmp % 10] += m*(y + 1); 19 tmp /= 10; 20 } 21 if (x) solve(x - 1, m * 10); 22 } 23 24 int main() { 25 while (cin >> l >> r && (l || r)) { 26 memset(b, 0, sizeof(b)); 27 if (l > r)swap(l, r); 28 solve(l - 1, 1); 29 for (int i = 0; i <= 9; i++)a[i] = b[i], b[i] = 0; 30 solve(r, 1); 31 cout << b[0] - a[0]; 32 for (int i = 1; i <= 9; i++)cout << " " << b[i] - a[i]; 33 cout << endl; 34 } 35 return 0; 36 }
Uva1641
题意:给出一个由 ‘ ‘,‘ . ‘, ‘ / ‘构成的图形,问这个图形的面积是多少
解法:对于’/‘或者’‘,每个对面积的贡献是0.5,对于‘.’来说从左到右,从上到下,判断之前括号的个数是否为奇数即可,如果是奇数则说明在图形内,反之亦然
1 #include<cstdio> 2 using namespace std; 3 const int maxn = 1e2 + 5; 4 char c[maxn][maxn]; 5 int h, w; 6 int main() { 7 while (scanf("%d%d", &h, &w)!=EOF) { 8 double ans = 0.0;int cnt = 0; 9 getchar(); 10 for (int i = 0; i < h; i++) { 11 for (int j = 0; j < w; j++) { 12 scanf("%c", &c[i][j]); 13 if (c[i][j] != ‘.‘) ans += 0.5,cnt++; 14 else {if (cnt & 1)ans += 1; } 15 } 16 getchar(); 17 } 18 printf("%d ",(int)ans); 19 } 20 return 0; 21 }
Uva1363
题意:
输入正整数n和k(范围均为1e9),求∑(k mod i),i从1~n
解法:
首先这道题直接暴力亲测会超时。
之后我们写几组数据之后可以发现当k/i的商相同的时候他们的余数成一个等差数列,而且数列首相是q,公差是p,项的个数是余数/商。
具体写法网上面有分情况讨论的,但是较为繁琐,这里LRJ的板子感觉写法就很精炼。
我们从左到右依次枚举每一项i(核心思想是减少i的枚举个数),计算出k除以这个数的商和余数, 如果这个商是0,说明此时的i已经大于k;如果不为0(即大于0),即来计算等差的数列的值。
如果k%i==0,则项的个数为0,计算和之后为0,其他情况就很正常了。
1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 typedef long long ll; 5 ll series_sum(int p, int d, int n) { return (ll)(2 * p - n*d)*(n + 1) / 2; } 6 int main() { 7 int n, k; 8 while (scanf("%d%d", &n, &k) != EOF) { 9 ll ans = 0, i = 1; 10 while (i <= n) { 11 int p = k / i, q = k%i; 12 int cnt = n - i; 13 if (p > 0)cnt = min(cnt, q / p);//计算项的个数,避免超出n的范围 14 ans += series_sum(q, p, cnt); 15 i += cnt + 1; 16 } 17 printf("%lld ", ans); 18 } 19 return 0; 20 }
以上是关于8.21总结前日及今日的主要内容,如果未能解决你的问题,请参考以下文章