2017福建省赛 FZU2272~2283
Posted buerdepepeqi
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2017福建省赛 FZU2272~2283相关的知识,希望对你有一定的参考价值。
1.FZU2272 Frog
传送门:http://acm.fzu.edu.cn/problem.php?pid=2272
题意:鸡兔同笼通解
题解:解一个方程组直接输出就行
代码如下:

#include <map> #include <set> #include <cmath> #include <ctime> #include <stack> #include <queue> #include <cstdio> #include <cctype> #include <bitset> #include <string> #include <vector> #include <cstring> #include <iostream> #include <algorithm> #include <functional> #define fuck(x) cout<<"["<<x<<"]"; #define FIN freopen("input.txt","r",stdin); #define FOUT freopen("output.txt","w+",stdout); //#pragma comment(linker, "/STACK:102400000,102400000") using namespace std; typedef long long LL; typedef pair<int, int> PII; const int maxn = 1e5+5; const int INF = 0x3f3f3f3f; const int MOD = 1e9+7; int main(){ #ifndef ONLINE_JUDGE FIN #endif int T; scanf("%d",&T); while(T--){ int n,m; cin>>n>>m; cout<<m/2-n<<" "<<2*n-m/2<<endl; } }
2.FZU2273
传送门:http://acm.fzu.edu.cn/problem.php?pid=2273
题意:给你两个三角形,让你判断三角形是相交,相离,还是包含
题解:计算几何模板题,先判断三角形A有没有点在三角形B里面,三角形B有没有点在三角形A里面,然后分情况讨论即可
代码如下:

#include<iostream> #include<cmath> using namespace std; struct point{ int x,y; }s[5][5]; double m(point a,point b,point c) //叉积 { return ((b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x)); } bool Judge(point u1,point u2,point v1,point v2) //判断两条线段相交情况 { return (max(u1.x,u2.x)>=min(v1.x,v2.x)&& max(u1.y,u2.y)>=min(v1.y,v2.y)&& max(v1.x,v2.x)>=min(u1.x,u2.x)&& max(v1.y,v2.y)>=min(u1.y,u2.y)&& m(u1,v1,u2)*m(u1,u2,v2)>=0&& m(v1,u1,v2)*m(v1,v2,u2)>=0); } int line_check(int p,int q) //判断两个三角形是否相交 { return (Judge(s[p][0],s[p][1],s[q][0],s[q][1])|| Judge(s[p][0],s[p][1],s[q][1],s[q][2])|| Judge(s[p][0],s[p][1],s[q][0],s[q][2])|| Judge(s[p][1],s[p][2],s[q][0],s[q][1])|| Judge(s[p][1],s[p][2],s[q][1],s[q][2])|| Judge(s[p][1],s[p][2],s[q][0],s[q][2])|| Judge(s[p][0],s[p][2],s[q][0],s[q][1])|| Judge(s[p][0],s[p][2],s[q][1],s[q][2])|| Judge(s[p][0],s[p][2],s[q][0],s[q][2])); } int point_check(int p,int q) // 面积法判断点在三角形内 { double res=fabs(m(s[q][0],s[q][1],s[q][2])); int ans=0; for(int i=0;i<3;i++) { double res1=fabs(m(s[q][0],s[q][1],s[p][i])); double res2=fabs(m(s[q][1],s[q][2],s[p][i])); double res3=fabs(m(s[q][0],s[q][2],s[p][i])); if(res1+res2+res3==res) ans++; } return ans; } int main() { int t; cin>>t; while(t--) { for(int i=0;i<2;i++) for(int j=0;j<3;j++) cin>>s[i][j].x>>s[i][j].y; int ans1=point_check(0,1),ans2=point_check(1,0); if(ans1==0&&ans2==0) //如果两个三角形没有一个点在另一个三角形内 { int ans=line_check(0,1); if(ans==0) cout<<"disjoint"<<endl; // 相离 else cout<<"intersect"<<endl; //相交 } else if(ans1==3||ans2==3) cout<<"contain"<<endl; //否则包含 else cout<<"intersect"<<endl; //相交 } return 0; }
3.FZU2275
传送门:http://acm.fzu.edu.cn/problem.php?pid=2275
题意:Alice有数字A,Bob有数字B,他们两个人可以对数字进行 1.删除最后一个数,2.将整个数字反转这两个操作,Alice想要将她的数字变得和Bob一样,Bob不想Alice的数字变得和她的一样,最后如果Alice变得和Bob一样了,则Alice赢,否则Bob赢,问你谁会赢
题解:1.如果Bob长度比Alice的数字长度长的话,Bob只需要不断反转他的数字即可,Alice不可能赢
2.如果Bob的数字为0的话,Alice一定赢
3.如果Bob的数字是Alice的数字的子串或者Bob数字的反转是Alice数字的子串的话,那么Alice一定赢
代码如下:

#include <map> #include <set> #include <cmath> #include <ctime> #include <stack> #include <queue> #include <cstdio> #include <cctype> #include <bitset> #include <string> #include <vector> #include <cstring> #include <iostream> #include <algorithm> #include <functional> #define fuck(x) cout<<"["<<x<<"]"; #define FIN freopen("input.txt","r",stdin); #define FOUT freopen("output.txt","w+",stdout); //#pragma comment(linker, "/STACK:102400000,102400000") using namespace std; typedef long long LL; typedef pair<int, int> PII; const int maxn = 1e5+5; const int INF = 0x3f3f3f3f; const int MOD = 1e9+7; int Nxt[maxn]; void makeNext(char P[]) { int m = strlen(P); Nxt[0] = 0; for (int q = 1, k = 0; q < m; ++q) { while (k > 0 && P[q] != P[k]) k = Nxt[k - 1]; if (P[q] == P[k]) k++; Nxt[q] = k; } } int kmp(char T[], char P[]) { int n = strlen(T), m = strlen(P); makeNext(P); for (int i = 0, q = 0; i < n; ++i) { while (q > 0 && P[q] != T[i]) q = Nxt[q - 1]; if (P[q] == T[i]) q++; if (q == m) return i - m + 1; //?¥??3é1|,·μ??3é1|ê±ê×???? } return -1;//?¥??꧰ü } int main(){ #ifndef ONLINE_JUDGE FIN #endif char str1[maxn]; char str2[maxn]; char str3[maxn]; int T; scanf("%d",&T); while(T--){ cin>>str1>>str2; int len1=strlen(str1); int len2=strlen(str2); for(int i=0;i<len2;i++){ str3[len2-i-1]=str2[i]; } if(len2==1&&str2[0]==‘0‘){ cout<<"Alice"<<endl; continue; } str3[len2]=‘�‘; if(len1<len2){ cout<<"Bob"<<endl; }else{ int ans1=kmp(str1,str2); int ans2=kmp(str1,str3); if(ans1!=-1||ans2!=-1){ cout<<"Alice"<<endl; }else cout<<"Bob"<<endl; } } }
4.FZU2277
传送门:http://acm.fzu.edu.cn/problem.php?pid=2277
题意:给你一颗树的结构,有两种操作,1.将给定节点和这个节点的所有子树上的权值 value += x-deep*k ,2.询问这个节点的权值
题解:线段树和的dfs序,线段树维护该区间节点的权值,dfs序修改其子树的权值,具体题解看代码注释
代码如下:

#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define fuck(x) cout<<"["<<x<<"]"; #define FIN freopen("input.txt","r",stdin); #define FOUT freopen("output.txt","w+",stdout); #define lson root<<1 #define rson root<<1|1 #pragma comment(linker, "/STACK:102400000,102400000") using namespace std; typedef long long LL; typedef pair<int, int> PII; const int maxn = 8e5+7; const int INF = 0x3f3f3f3f; const int mod = 1e9+7; int n,q; struct node{ int l,r; LL sum1;//sum1记录需要加上来的数 LL sum2;//sum2记录需要减去的数 }Tree[maxn<<2]; int ltid[maxn]; //更新的左区间 int rtid[maxn]; //更新的右区间 int dep[maxn]; //维护每个节点的深度 struct E{ int v,next; }edge[maxn]; int head[maxn]; int tot,top; //前向星建图 inline void add(int u,int v){ edge[tot].v=v; edge[tot].next=head[u]; head[u]=tot++; } //dfs序查询子树的点权和 void dfs(int u,int deep){ ltid[u]=++top; dep[u]=deep; for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].v; dfs(v,deep+1); } rtid[u]=top; //这样从左到右的一段区间了【lrid,rtid】就表示了节点u的子树权值 return; } //建树,节点value值初始化为0 void build(int l,int r ,int root){ Tree[root].l=l; Tree[root].r=r; Tree[root].sum1=Tree[root].sum2=0; if(l==r) return; int mid=(l+r)>>1; build(l,mid,lson); build(mid+1,r,rson); } void Add(LL &a,LL b){ a+=b; a%=mod; } //更新节点和子树的sum1和sum2 void push_down(int root){ LL a=Tree[root].sum1; LL b=Tree[root].sum2; if(a) Add(Tree[lson].sum1,a); if(a) Add(Tree[rson].sum1,a); if(b) Add(Tree[lson].sum2,b); if(b) Add(Tree[rson].sum2,b); Tree[root].sum1=Tree[root].sum2=0; } void update(int L,int R,LL x,LL k,int root){ int l=Tree[root].l; int r=Tree[root].r; int mid=(l+r)/2; if(L<=l&&r<=R){ //到了需要更改的区间 Add(Tree[root].sum1,x); //sum1加上x Add(Tree[root].sum2,k); //sum2加上k return; } //更新树 push_down(root); //更新区间 if(L>mid) update(L,R,x,k,rson); else if(R<=mid) update(L,R,x,k,lson); else { update(L,mid,x,k,lson); update(mid+1,R,x,k,rson); } } LL query(int p,int deep,int root){ if(Tree[root].l==Tree[root].r){ //查询值为 ai+=x-k*deep return ((Tree[root].sum1-Tree[root].sum2*deep%mod)+mod)%mod; } push_down(root); int mid=(Tree[root].l+Tree[root].r)/2; if(p<=mid) return query(p,deep,lson); return query(p,deep,rson); } int main(){ int T; scanf("%d",&T); while(T--){ scanf("%d",&n); memset(head,-1,sizeof(head)); tot=0;top=0; int u; for(int i=2;i<=n;i++){ scanf("%d",&u); add(u,i); } dfs(1,1); build(1,n,1); int op,v,x,k; scanf("%d",&q); while(q--){ scanf("%d",&op); if(op==1){ scanf("%d%d%d",&v,&x,&k); //注意 因为会出现负数,所以我们每次减的操作变成+,最后查询的时候再减 //用两个值分别存所需要加的数和所需要减的数,最后查询的时候操作即可 update(ltid[v],rtid[v],(x*1LL+dep[v]*1LL*k%mod)%mod,k,1); }else{ scanf("%d",&v); //查询时用 printf("%lld ",query(ltid[v],dep[v],1)); } } } return 0; }
5.FZU2278
传送门:http://acm.fzu.edu.cn/problem.php?pid=2278
题意:有n张牌需要你去抽,每次抽牌的概率是一样的,你每过(n-1)!天可以抽一张牌,求抽齐所有牌的数学期望值
题解:如果我有a张卡,那么我抽到第a+1张卡的概率是(n-a)/n,那么我抽到第a+1张卡平均就需要n/(n-a)天,每隔(n-1)!天就可以抽一次牌
那么我们最后推出来公式就是(n-1)!*n(1+1/2+1/3+……1/n),因为数字特别大,我们要用到大数的知识
三种写法:
1.c++的大数模板
2.Java 的Bignumber
3.python直接写 果然py是最强的
代码如下:

#include <map> #include <set> #include <cmath> #include <ctime> #include <stack> #include <queue> #include <cstdio> #include <cctype> #include <bitset> #include <string> #include <vector> #include <cstring> #include <iostream> #include <algorithm> #include <functional> using namespace std; #define MAXN 9999 #define MAXSIZE 10 #define DLEN 4 class BigNum { private: int a[20005]; //可以控制大数的位数 int len; //大数长度 public: BigNum(){ len = 1;memset(a,0,sizeof(a)); } //构造函数 BigNum(const int); //将一个int类型的变量转化为大数 BigNum(const char*); //将一个字符串类型的变量转化为大数 BigNum(const BigNum &); //拷贝构造函数 BigNum &operator=(const BigNum &); //重载赋值运算符,大数之间进行赋值运算 friend istream& operator>>(istream&, BigNum&); //重载输入运算符 friend ostream& operator<<(ostream&, BigNum&); //重载输出运算符 BigNum operator+(const BigNum &) const; //重载加法运算符,两个大数之间的相加运算 BigNum operator-(const BigNum &) const; //重载减法运算符,两个大数之间的相减运算 BigNum operator*(const BigNum &) const; //重载乘法运算符,两个大数之间的相乘运算 BigNum operator/(const int &) const; //重载除法运算符,大数对一个整数进行相除运算 BigNum operator^(const int &) const; //大数的n次方运算 int operator%(const int &) const; //大数对一个int类型的变量进行取模运算 bool operator>(const BigNum & T)const; //大数和另一个大数的大小比较 bool operator>(const int & t)const; //大数和一个int类型的变量的大小比较 void print(); //输出大数 }; BigNum::BigNum(const int b) //将一个int类型的变量转化为大数 { int c,d = b; len = 0; memset(a,0,sizeof(a)); while(d > MAXN) { c = d - (d / (MAXN + 1)) * (MAXN + 1); d = d / (MAXN + 1); a[len++] = c; } a[len++] = d; } BigNum::BigNum(const char*s) //将一个字符串类型的变量转化为大数 { int t,k,index,l,i; memset(a,0,sizeof(a)); l=strlen(s); len=l/DLEN; if(l%DLEN) len++; index=0; for(i=l-1;i>=0;i-=DLEN) { t=0; k=i-DLEN+1; if(k<0) k=0; for(int j=k;j<=i;j++) t=t*10+s[j]-‘0‘; a[index++]=t; } } BigNum::BigNum(const BigNum & T) : len(T.len) //拷贝构造函数 { int i; memset(a,0,sizeof(a)); for(i = 0 ; i < len ; i++) a[i] = T.a[i]; } BigNum & BigNum::operator=(const BigNum & n) //重载赋值运算符,大数之间进行赋值运算 { int i; len = n.len; memset(a,0,sizeof(a)); for(i = 0 ; i < len ; i++) a[i] = n.a[i]; return *this; } istream& operator>>(istream & in, BigNum & b) //重载输入运算符 { char ch[MAXSIZE*4]; int i = -1; in>>ch; int l=strlen(ch); int count=0,sum=0; for(i=l-1;i>=0;) { sum = 0; int t=1; for(int j=0;j<4&&i>=0;j++,i--,t*=10) { sum+=(ch[i]-‘0‘)*t; } b.a[count]=sum; count++; } b.len =count++; return in; } ostream& operator<<(ostream& out, BigNum& b) //重载输出运算符 { int i; cout << b.a[b.len - 1]; for(i = b.len - 2 ; i >= 0 ; i--) { cout.width(DLEN); cout.fill(‘0‘); cout << b.a[i]; } return out; } BigNum BigNum::operator+(const BigNum & T) const //两个大数之间的相加运算 { BigNum t(*this); int i,big; //位数 big = T.len > len ? T.len : len; for(i = 0 ; i < big ; i++) { t.a[i] +=T.a[i]; if(t.a[i] > MAXN) { t.a[i + 1]++; t.a[i] -=MAXN+1; } } if(t.a[big] != 0) t.len = big + 1; else t.len = big; return t; } BigNum BigNum::operator-(const BigNum & T) const //两个大数之间的相减运算 { int i,j,big; bool flag; BigNum t1,t2; if(*this>T) { t1=*this; t2=T; flag=0; } else { t1=T; t2=*this; flag=1; } big=t1.len; for(i = 0 ; i < big ; i++) { if(t1.a[i] < t2.a[i]) { j = i + 1; while(t1.a[j] == 0) j++; t1.a[j--]--; while(j > i) t1.a[j--] += MAXN; t1.a[i] += MAXN + 1 - t2.a[i]; } else t1.a[i] -= t2.a[i]; } t1.len = big; while(t1.a[len - 1] == 0 && t1.len > 1) { t1.len--; big--; } if(flag) t1.a[big-1]=0-t1.a[big-1]; return t1; } BigNum BigNum::operator*(const BigNum & T) const //两个大数之间的相乘运算 { BigNum ret; int i,j,up; int temp,temp1; for(i = 0 ; i < len ; i++) { up = 0; for(j = 0 ; j < T.len ; j++) { temp = a[i] * T.a[j] + ret.a[i + j] + up; if(temp > MAXN) { temp1 = temp - temp / (MAXN + 1) * (MAXN + 1); up = temp / (MAXN + 1); ret.a[i + j] = temp1; } else { up = 0; ret.a[i + j] = temp; } } if(up != 0) ret.a[i + j] = up; } ret.len = i + j; while(ret.a[ret.len - 1] == 0 && ret.len > 1) ret.len--; return ret; } BigNum BigNum::operator/(const int & b) const //大数对一个整数进行相除运算 { BigNum ret; int i,down = 0; for(i = len - 1 ; i >= 0 ; i--) { ret.a[i] = (a[i] + down * (MAXN + 1)) / b; down = a[i] + down * (MAXN + 1) - ret.a[i] * b; } ret.len = len; while(ret.a[ret.len - 1] == 0 && ret.len > 1) ret.len--; return ret; } int BigNum::operator %(const int & b) const //大数对一个int类型的变量进行取模运算 { int i,d=0; for (i = len-1; i>=0; i--) { d = ((d * (MAXN+1))% b + a[i])% b; } return d; } BigNum BigNum::operator^(const int & n) const //大数的n次方运算 { BigNum t,ret(1); int i; if(n<0) exit(-1); if(n==0) return 1; if(n==1) return *this; int m=n; while(m>1) { t=*this; for( i=1;i<<1<=m;i<<=1) { t=t*t; } m-=i; ret=ret*t; if(m==1) ret=ret*(*this); } return ret; } bool BigNum::operator>(const BigNum & T) const //大数和另一个大数的大小比较 { int ln; if(len > T.len) return true; else if(len == T.len) { ln = len - 1; while(a[ln] == T.a[ln] && ln >= 0) ln--; if(ln >= 0 && a[ln] > T.a[ln]) return true; else return false; } else return false; } bool BigNum::operator >(const int & t) const //大数和一个int类型的变量的大小比较 { BigNum b(t); return *this>b; } void BigNum::print() //输出大数 { int i; cout << a[len - 1]; for(i = len - 2 ; i >= 0 ; i--) { cout.width(DLEN); cout.fill(‘0‘); cout << a[i]; } } int main(void) { int i,n; int T; cin>>T; while(T--){ BigNum x; //定义大数的对象数组 BigNum ans; int n; cin>>n; x=1; for(int i=1;i<=n;i++){ x=x*i; } for(int i=1;i<=n;i++){ ans=ans+(x/i); } ans.print(); cout<<".0"<<endl; } }

import java.util.*; import java.math.*; public class Main { public static void main(String[] args) { int t; Scanner sc=new Scanner(System.in); t=sc.nextInt(); for(int cc=0;cc<t;cc++) { BigInteger b=BigInteger.valueOf(1); int n; n=sc.nextInt(); for(int i=1;i<=n;i++) { b=b.multiply(BigInteger.valueOf(i)); } BigInteger d=BigInteger.valueOf(0); for(int i=1;i<=n;i++) { BigInteger mm=b.divide(BigInteger.valueOf(i)); d=d.add(mm); } System.out.println(d+".0"); } } }
6.FZU2281
传送门:http://acm.fzu.edu.cn/problem.php?pid=2281
题意:你手上有m元,可以买和卖货物,货物在n天的价格各不相同,求你n天过后最多可以有多少钱
题解:将货物的价格画成一个曲线,那么我们就可以发现,我们需要在货物价格低的时候买,价格高的时候卖,因为有多个波谷和波峰,就需要对每一个波谷和波峰进行买和卖的操作,这题也是大数,需要用到大数模板
代码如下:

#include <map> #include <set> #include <cmath> #include <ctime> #include <stack> #include <queue> #include <cstdio> #include <cctype> #include <bitset> #include <string> #include <vector> #include <cstring> #include <iostream> #include <algorithm> #include <functional> #define fuck(x) cout<<"["<<x<<"]"; #define FIN freopen("input.txt","r",stdin); #define FOUT freopen("output.txt","w+",stdout); //#pragma comment(linker, "/STACK:102400000,102400000") using namespace std; typedef long long LL; typedef pair<int, int> PII; const int maxn = 3e3+5; const int INF = 0x3f3f3f3f; const int mod = 1e9+7; const int MAXL = 6e3+5; const int MAXN = 9999; const int DLEN = 4; class Big { public: int a[MAXL], len; Big(const int b = 0) { int c, d = b; len = 0; memset(a, 0, sizeof(a)); while(d > MAXN) { c = d - (d / (MAXN + 1)) * (MAXN + 1); d = d / (MAXN + 1); a[len++] = c; } a[len++] = d; } Big(const char *s) { int t, k, index, L; memset(a, 0, sizeof(a)); L = strlen(s); len = L / DLEN; if(L % DLEN) len++; index = 0; for(int i = L - 1; i >= 0; i -= DLEN) { t = 0; k = i - DLEN + 1; if(k < 0) k = 0; for(int j = k; j <= i; j++) t = t * 10 + s[j] - ‘0‘; a[index++] = t; } } Big operator/(const LL &b)const { Big ret; LL down = 0; for(int i = len - 1; i >= 0; i--) { ret.a[i] = (a[i] + down * (MAXN + 1)) / b; down = a[i] + down * (MAXN + 1) - ret.a[i] * b; } ret.len = len; while(ret.a[ret.len - 1] == 0 && ret.len > 1) ret.len--; return ret; } bool operator>(const Big &T)const { int ln; if(len > T.len) return true; else if(len == T.len) { ln = len - 1; while(a[ln] == T.a[ln] && ln >= 0) ln--; if(ln >= 0 && a[ln] > T.a[ln]) return true; else return false; } else return false; } Big operator+(const Big &T)const { Big t(*this); int big = T.len > len ? T.len : len; for(int i = 0; i < big; i++) { t.a[i] += T.a[i]; if(t.a[i] > MAXN) { t.a[i + 1]++; t.a[i] -= MAXN + 1; } } if(t.a[big] != 0) t.len = big + 1; else t.len = big; return t; } Big operator-(const Big &T)const { int big; bool flag; Big t1, t2; if(*this > T) { t1 = *this; t2 = T; flag = 0; } else { t1 = T; t2 = *this; flag = 1; } big = t1.len; for(int i = 0; i < big; i++) { if(t1.a[i] < t2.a[i]) { int j = i + 1; while(t1.a[j] == 0) j++; t1.a[j--]--; while(j > i) t1.a[j--] += MAXN; t1.a[i] += MAXN + 1 - t2.a[i]; } else t1.a[i] -= t2.a[i]; } t1.len = big; while(t1.a[t1.len - 1] == 0 && t1.len > 1) { t1.len--; big--; } if(flag) t1.a[big - 1] = 0 - t1.a[big - 1]; return t1; } LL operator%(const int &b)const { LL d = 0; for(int i = len - 1; i >= 0; i--) d = ((d * (MAXN + 1)) % b + a[i]) % b; return d; } Big operator*(const Big &T) const { Big ret; int i, j, up, temp, temp1; for(i = 0; i < len; i++) { up = 0; for(j = 0; j < T.len; j++) { temp = a[i] * T.a[j] + ret.a[i + j] + up; if(temp > MAXN) { temp1 = temp - temp / (MAXN + 1) * (MAXN + 1); up = temp / (MAXN + 1); ret.a[i + j] = temp1; } else { up = 0; ret.a[i + j] = temp; } } if(up != 0) ret.a[i + j] = up; } ret.len = i + j; while(ret.a[ret.len - 1] == 0 && ret.len > 1) ret.len--; return ret; } void print() { printf("%d", a[len - 1]); for(int i = len - 2; i >= 0; i--) printf("%04d", a[i]); } }; int a[maxn]; int main(){ int T; int cas=1; scanf("%d",&T); while(T--){ int n,m; printf("Case #%d: ",cas++); scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ scanf("%d",&a[i]); } if(m==0){ printf("0 "); continue; } Big ans=m; int by=n; for(int i=1;i<n;i++){ if(a[i+1]>a[i]){ by=i; break; } } if(by<n){ Big x=ans/a[by],y=ans%a[by]; while(by<n){ int sl=by+1; while(sl<n&&a[sl+1]>=a[sl]) sl++; if(sl==n){ ans=x*a[sl]+y; break; }else{ ans=x*a[sl]+y; by=sl+1; while(by<n&&a[by]>=a[by+1]) by++; if(by<n) x=ans/a[by],y=ans%a[by]; } } } LL x=ans%mod; cout<<x<<endl; } }
7.FZU2282
传送门:http://acm.fzu.edu.cn/problem.php?pid=2282
题意:有一个1~n的全排列,你需要对他进行操作,使得至少有k个人的位置在原来的位置,而剩下的人不在本身的位置
题解:错位排列,公式: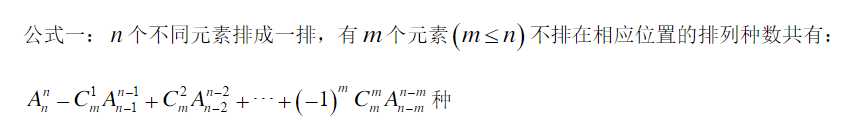
代码如下:

#include <map> #include <set> #include <cmath> #include <ctime> #include <stack> #include <queue> #include <cstdio> #include <cctype> #include <bitset> #include <string> #include <vector> #include <cstring> #include <iostream> #include <algorithm> #include <functional> #define fuck(x) cout<<"["<<x<<"]"; #define FIN freopen("input.txt","r",stdin); #define FOUT freopen("output.txt","w+",stdout); //#pragma comment(linker, "/STACK:102400000,102400000") using namespace std; typedef long long LL; typedef pair<int, int> PII; const int maxn = 1e5+5; const int INF = 0x3f3f3f3f; const int mod = 1e9+7; LL Jc[maxn]; LL c[maxn]; void calJc() //求maxn以内的数的阶乘 { Jc[0] = Jc[1] = 1; Jc[2]=2; c[0]=1; c[1]=0; c[2]=1; for(LL i = 3; i < maxn; i++){ c[i]=(((i-1)%mod)*((c[i-1]+c[i-2])%mod))%mod; Jc[i] = Jc[i - 1] * i % mod; } } //费马小定理求逆元 LL pow(LL a, LL n, LL p) //快速幂 a^n % p { LL ans = 1; while(n) { if(n & 1) ans = ans * a % p; a = a * a % p; n >>= 1; } return ans; } LL niYuan(LL a, LL b) //费马小定理求逆元 { return pow(a, b - 2, b); } LL C(LL a, LL b) //计算C(a, b) { return Jc[a] * niYuan(Jc[b], mod) % mod* niYuan(Jc[a - b], mod) % mod; } int main(){ calJc(); int T; scanf("%d",&T); while(T--){ int n,k; scanf("%d%d",&n,&k); LL ans=0; for(int i=0;i<k;i++){ ans=((ans%mod)+(C(n,i)*c[n-i])%mod)%mod; } printf("%lld ",(mod+Jc[n]%mod-ans%mod)%mod); } }
8.FZU2283
传送门:http://acm.fzu.edu.cn/problem.php?pid=2283
题意:玩 x棋,Kim先手,给你当前场上的局势和Kim的棋子,每个人都走最优步,问谁可以赢
题解:玩过这个游戏的都知道,只要你场上还有足够的空间并且你占据了中心的那个格子,你是一定赢的,如果不知道为什么,多玩几把就行,所以我们只需要数场上的空格和判断中心即可
代码如下:

#include <map> #include <set> #include <cmath> #include <ctime> #include <stack> #include <queue> #include <cstdio> #include <cctype> #include <bitset> #include <string> #include <vector> #include <cstring> #include <iostream> #include <algorithm> #include <functional> #define fuck(x) cout<<"["<<x<<"]"; #define FIN freopen("input.txt","r",stdin); #define FOUT freopen("output.txt","w+",stdout); //#pragma comment(linker, "/STACK:102400000,102400000") using namespace std; typedef long long LL; typedef pair<int, int> PII; const int maxn = 1e5+5; const int INF = 0x3f3f3f3f; const int MOD = 1e9+7; char mp[4][4]; int main(){ #ifndef ONLINE_JUDGE FIN #endif int T; cin>>T; while(T--){ char ch; int cnt=0; for(int i=0;i<3;i++){ for(int j=0;j<3;j++){ cin>>mp[i][j]; if(mp[i][j]==‘.‘) cnt++; } } cin>>ch; int flag; if(cnt<=5){ if(mp[1][1]==ch||mp[1][1]==‘.‘) flag=1; else flag=0; }else flag=0; if(flag) cout<<"Kim win!"<<endl; else cout<<"Cannot win!"<<endl; } }
以后一定好好写线段树嘤嘤嘤
以上是关于2017福建省赛 FZU2272~2283的主要内容,如果未能解决你的问题,请参考以下文章
