函数式编程之-重新认识泛型

Posted 2020-12-30 xiandnc

回顾上一节，为了丰富建模类型，编程语言引入了泛型，例如Optional<T>，Result<T>等。我们把泛型也叫做类型提升(lifting)，这样带来的问题是以往的函数不能再适应提升类型，试想之前已经存在一个a->b的函数，但是此时你拥有一个E<a>变量，你无法直接把E<a>传入到a->b的函数中。上一节还提到，一旦你的类型被提升(lifting)，你应该竟可能的让他保持在提升的状态，而不是随意在提升类型(E<a>)和a直接来回切换。

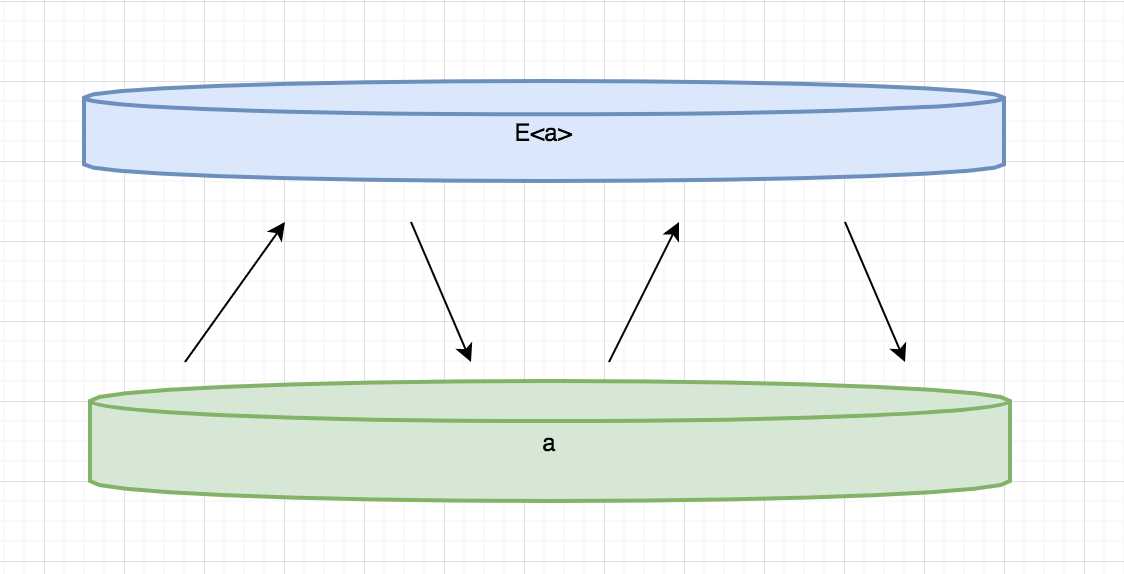
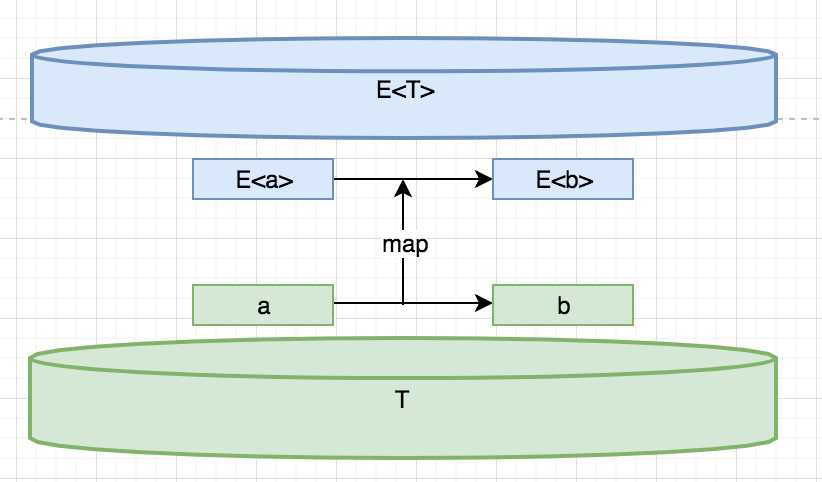
为了达到这个目的，数学家们发现了一些规律，通过一些函数来达到这个目的。例如:当你已经有一个定义好的函数a->b，而这时候又有一个被提升的类型E<a>，此时你可以通过map/select函数直接将a->b应用在E<a>上得到E<b>。

从某种意义上来说，map/select函数有提升函数的作用。之所以a->b可以作用在E<a>上面，是因为map/select函数把函数a->b提升为E<a->b>。正因为如此，某些语言也将map函数叫做lift函数。

return函数

在继续往下介绍之前，我们先了解另一个函数return，有的语言也称为pure/unit/point。

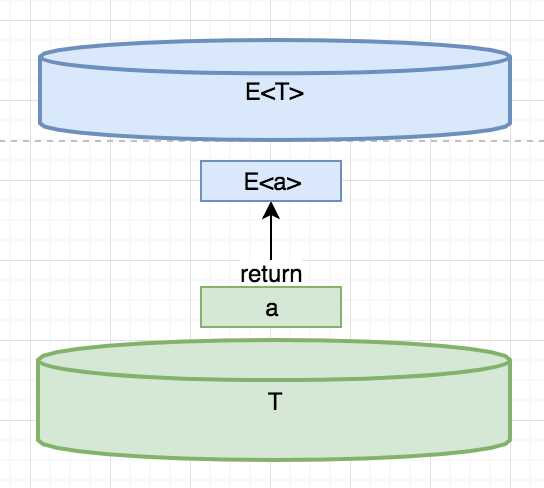
return函数的作用在于将普通类型a提升为E<a>。例如下面的C#代码：

var x = Optional.Some(10); //将int提升为Optional<int>
var y = Optional.None<int>; //将int提升为Optional<int>
var z = new List<int>(){1,2,3}; //将int提升为List<int>

一般来说你并不需要单独定义return函数，但是当我们提到return函数的时候你应该要知道他的意图。

通过map函数来提升函数

除了return函数能够提升类型，map函数也有提升类型的作用。
考虑下面的情况：

let add1 x = x + 1
let result = Some 2 |> Option.map add1

给定一个函数add1: a->b，然后通过Option.map将add1提升为E<(a->b)>，并传入Some 2，得到结果Some 3。
上面的函数add1只有一个参数，如果对两个拥有参数的函数做map会发生什么？

let add x y = x + y
let result' = Some 2 |> Option.map add

因为add接受两个参数x和y，通过map提升并传入第一个参数Some 2，得到的结果result‘是一个提升函数Option<(a->b)>。C#并不支持这种方式，C#中的Select方法只接受Func<TSource, TResult>，也就是说C#中的Select方法只接受一个参数的函数。你不能通过Select提升具有多个参数的函数。
同理，通过map提升拥有3个参数的函数:

let add x y z = x + y + z
let result' = Some 2 |> Option.map add

得到的result‘是Option<(a->b->c)>。

apply函数

对于普通类型的函数a->b->c，你可以通过partial应用依次传入a和b，最终得到c。

//定义一个函数 add: a -> b -> c
let add a b =
    a + b
    
let add10 = add 10  // add10: b -> c
let result = add10 2 // result: 12

我们已经知道有两种途径可以提升函数：return和map，那么：
假如你有一个Option<(a->b->c)>的函数，你能否在提升类型的世界里做partial应用呢？

// 通过return 函数创建一个提升函数Option<(a->b->c)>
let add' = Some (fun x y -> x + y) 
// 试图在add'函数上传入Some 2做partial application
let add2' = add' (Some 2)

上面的函数会发生编译失败，也就是说，对于一个提升函数，无法做partial application. 如果我们能够定义一个函数，他可以接受一个提升类型的函数和一个提升类型的参数，同时得到另一个提升类型的结果，那么我们的目的就达到了：

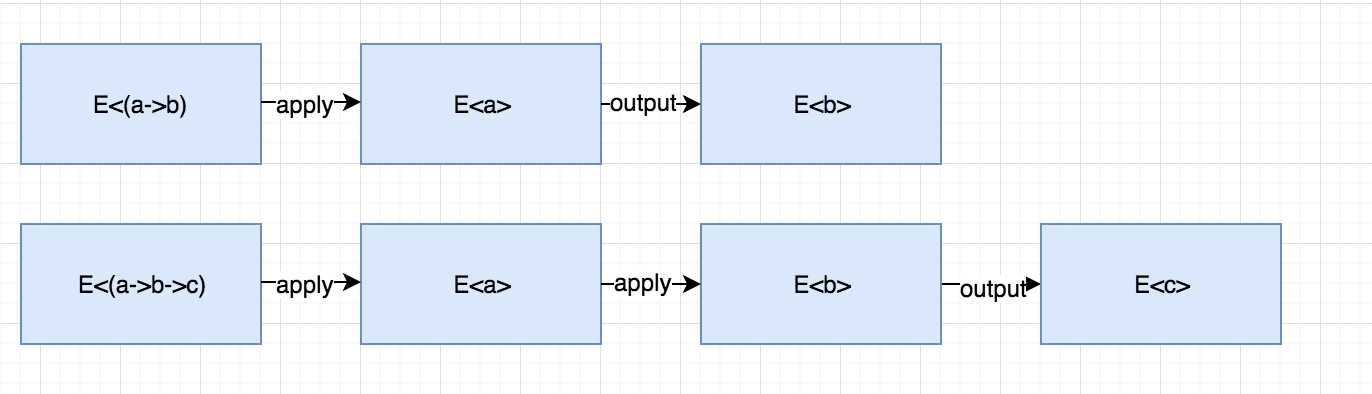
下面是Option<T>类型的apply定义：

module Option =
    let apply fOpt xOpt = 
        match fOpt,xOpt with
        | Some f, Some x -> Some (f x)
        | _ -> None

有了apply函数就可以对提升类型的函数做partial应用了：

let add' = Some (fun x y -> x + y) 
let add2' = Some 2 |> Option.apply add'
let add23' = Some 3 |> Option.apply add'2

中缀表达式

F#或者C#中的函数都是前缀表达式，例如有一个add函数，接受两个参数:

let add x y = x + y
let result = add x y // 函数名在前面，两个参数在后面

但是数学中的运算符通常都是中缀表达式，例如数学中的加号运算符：

let result = 1 + 2

加号写在中间，而两个参数分别写在两边。同样的道理，任意一个拥有两个参数的函数，我们都可以通过定义运算符的方式，让他变为中缀表达式，例如在F#通过下面的方式定义运算符：

let (<*>) = Option.apply

有了运算符<*>，上面的apply过程就可以写成下面的样子：

(Some add) <*> (Some 2) <*> (Some 3)

上面的代码通过return函数来提升函数，我们知道map函数也可以提升函数：

let (<!>) = Option.map
let (<*>) = Option.apply

add <!> (Some 2) <*> (Some 3)

跟Functor Laws一样，同样有四个所谓的"Applicative Laws"，这四个Laws我将不一一描述，从代码的角度来说，本文描述的apply函数就是所谓的Applicative Functor。

map2和map3函数

对于上面的实例，能够将拥有两个参数的函数提升，并且接受两个提升类型的过程，F#定义了一个函数叫做map2:

let result = Option.map2 add (Some 2) (Some 3)

同样的道理，如果是3个参数的函数，则可以通过map3函数来完成。

什么样的类型支持map/apply/return?

几乎所有你能用到的泛型都可以支持这三个函数，如果是你自己编写的泛型类型，请尝试添加这三个函数。

applicative和apply到底有什么用？

如果你看到这里你已经明白了什么是applicative，但是到底什么样的场景能够使用applicative呢？对于实际的软件工程到底有什么用呢？后来的文章将描述具体的用法，请持续关注。