K. Random Numbers（Gym 101466K + 线段树 + dfs序 + 快速幂 + 唯一分解）

Posted 2020-12-30 dillonh

题目链接：http://codeforces.com/gym/101466/problem/K

题目：

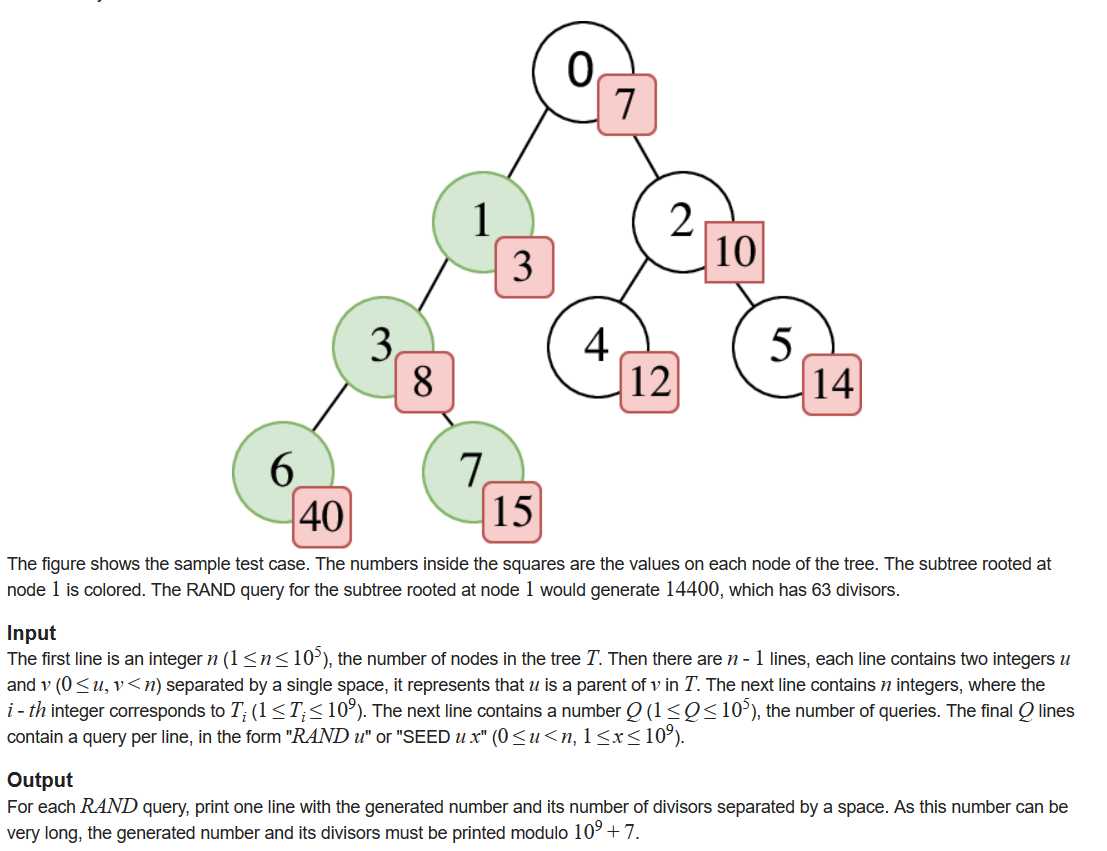
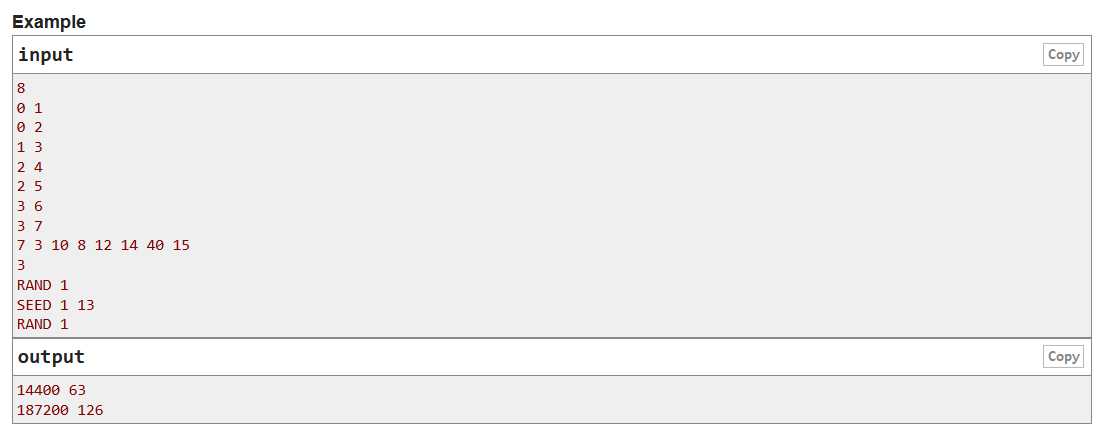
题意：

　　给你一棵有n个节点的树，根节点始终为0，有两种操作：

　　　　1.RAND：查询以u为根节点的子树上的所有节点的权值的乘积x，及x的因数个数。

　　　　2.SEED：将节点u的权值乘以x。

思路：

　　比赛时少看了因数不大于13这句话，然后本题难度增加数倍，肝了两个小时都没肝出来，对不起队友啊，今天的组队训练赛实力背锅……

　　这题一眼线段树，由于是对一棵子树进行处理，因此我们采用常规套路，借助dfs序将子树变成区间。不过因为权值的乘积太大，还要取模，一个数取模后因数个数也会发生变化，所以我们肯定不能用它的权值来进行建树，因而我们可以将思路进行转化，先将它的每个节点的权值进行唯一分解，对指数进行建树。

　　对于最后的答案，第一个乘积x很容易求，用快速幂对2，3，5，7，11，13这六个素数进行处理即可。而第二个答案，我们根据数论知识知道它的结果是∏（1+ci），其中ci为某个因数pi的指数。

代码实现如下：

  1 #include <set>
  2 #include <map>
  3 #include <queue>
  4 #include <stack>
  5 #include <cmath>
  6 #include <bitset>
  7 #include <cstdio>
  8 #include <string>
  9 #include <vector>
 10 #include <cstdlib>
 11 #include <cstring>
 12 #include <iostream>
 13 #include <algorithm>
 14 using namespace std;
 15 
 16 typedef long long ll;
 17 typedef pair<ll, ll> pll;
 18 typedef pair<ll, int> pli;
 19 typedef pair<int, ll> pil;;
 20 typedef pair<int, int> pii;
 21 typedef unsigned long long ull;
 22 
 23 #define lson i<<1
 24 #define rson i<<1|1
 25 #define lowbit(x) x&(-x)
 26 #define bug printf("*********
");
 27 #define debug(x) cout<<"["<<x<<"]" <<endl;
 28 #define FIN freopen("D://code//in.txt", "r", stdin);
 29 #define IO ios::sync_with_stdio(false),cin.tie(0);
 30 
 31 const double eps = 1e-8;
 32 const int mod = 1e9 + 7;
 33 const int maxn = 1e5 + 7;
 34 const int mx = 1e4 + 7;
 35 const double pi = acos(-1);
 36 const int inf = 0x3f3f3f3f;
 37 const ll INF = 0x3f3f3f3f3f3f3f3f;
 38 
 39 int n, tot, q, u, v, x, p, a, b;
 40 char op[10];
 41 int prime[6] = {2, 3, 5, 7, 11, 13}, cnt[6], ans[6];
 42 int val[maxn], head[maxn], s[maxn], t[maxn];
 43 
 44 struct edge {
 45     int v, next;
 46 }ed[maxn];
 47 
 48 struct node {
 49     int l, r;
 50     int num[6];
 51 }segtree[maxn<<2];
 52 
 53 void addedge(int u, int v) {
 54     ed[tot].v = v;
 55     ed[tot].next = head[u];
 56     head[u] = tot++;
 57 }
 58 
 59 void dfs(int u) {
 60     s[u] = ++x;
 61     for(int i = head[u]; ~i; i = ed[i].next) {
 62         int v = ed[i].v;
 63         dfs(v);
 64     }
 65     t[u] = x;
 66 }
 67 
 68 void push_up(int i) {
 69     for(int j = 0; j < 6; j++) {
 70         segtree[i].num[j] = (segtree[lson].num[j] + segtree[rson].num[j]) % mod;
 71     }
 72 }
 73 
 74 void build(int i, int l, int r) {
 75     segtree[i].l = l, segtree[i].r = r;
 76     for(int j = 0; j < 6; j++) {
 77         segtree[i].num[j] = 0;
 78     }
 79     if(l == r) {
 80         for(int j = 0; j < 6; j++) {
 81             if(val[l] % prime[j] == 0) {
 82                 while(val[l] % prime[j] == 0) {
 83                     segtree[i].num[j]++;
 84                     val[l] /= prime[j];
 85                 }
 86             }
 87         }
 88         return;
 89     }
 90     int mid = (l + r) >> 1;
 91     build(lson, l, mid);
 92     build(rson, mid + 1, r);
 93     push_up(i);
 94 }
 95 
 96 void update(int i, int pos, int cnt[]) {
 97     if(segtree[i].l == pos && segtree[i].r == pos) {
 98         for(int j = 0; j < 6; j++) {
 99             segtree[i].num[j] = (segtree[i].num[j] + cnt[j]) % mod;
100         }
101         return;
102     }
103     int mid = (segtree[i].l + segtree[i].r) >> 1;
104     if(pos <= mid) update(lson, pos, cnt);
105     else update(rson, pos, cnt);
106     push_up(i);
107 }
108 
109 int Mod_Pow(int x, int n) {
110     int res = 1;
111     while(n) {
112         if(n & 1) res = (ll) res * x % mod;
113         x = (ll)x * x % mod;
114         n >>= 1;
115     }
116     return res;
117 }
118 
119 void query(int i, int l, int r, int ans[]) {
120     if(segtree[i].l == l && segtree[i].r == r) {
121         for(int j = 0; j < 6; j++) {
122             ans[j] += segtree[i].num[j];
123         }
124         return;
125     }
126     int mid = (segtree[i].l + segtree[i].r) >> 1;
127     if(r <= mid) query(lson, l, r, ans);
128     else if(l > mid) query(rson, l, r, ans);
129     else {
130         query(lson, l, mid, ans);
131         query(rson, mid + 1, r, ans);
132     }
133 }
134 
135 int main() {
136     //FIN;
137     tot = x = 0;
138     memset(head, -1, sizeof(head));
139     scanf("%d", &n);
140     for(int i = 1; i < n; i++) {
141         scanf("%d%d", &u, &v);
142         u++, v++;
143         addedge(u, v);
144     }
145     dfs(1);
146     for(int i = 1; i <= n; i++) {
147         scanf("%d", &p);
148         val[s[i]] = p;
149     }
150     build(1, 1, n);
151     scanf("%d", &q);
152     while(q--) {
153         scanf("%s", op);
154         if(op[0] == ‘R‘) {
155             scanf("%d", &a);
156             a++;
157             for(int i = 0; i < 6; i++) ans[i] = 0;
158             query(1, s[a], t[a], ans);
159             ll cnt1 = 1, cnt2 = 1;
160             for(int i = 0; i < 6; i++) {
161                 cnt2 = (cnt2 * ((1 + ans[i]) % mod)) % mod;
162                 cnt1 = (cnt1 * Mod_Pow(prime[i], ans[i])) % mod;
163             }
164             printf("%lld %lld
", cnt1, cnt2);
165         } else {
166             scanf("%d%d", &a, &b);
167             a++;
168             for(int j = 0; j < 6; j++) {
169                 cnt[j] = 0;
170                 if(b % prime[j] == 0) {
171                     while(b % prime[j] == 0) {
172                         cnt[j]++;
173                         b /= prime[j];
174                     }
175                 }
176             }
177             update(1, s[a], cnt);
178         }
179     }
180     return 0;
181 }

 

以上是关于K. Random Numbers（Gym 101466K + 线段树 + dfs序 + 快速幂 + 唯一分解）的主要内容，如果未能解决你的问题，请参考以下文章

gym101102J Divisible Numbers（预处理）

GYM 102501 K. Birdwatching(bfs,思维)

GYM 102501 K. Birdwatching(bfs,思维)

GYM 100792 K. King's Rout(topo排序+逆向思维)

CF gym 101933 K. King's Colors(二项式反演)

Gym 101102J---Divisible Numbers(反推技巧题)