机器学习数学

Posted 2020-12-30 coolqiyu

参考：百度PaddlePaddle公开课

概率 & 统计

Lary Wasserman《All of Statistics》

概率：给定数据生成过程，那么输出的性质是怎样

统计：给定输出结果，那么生成数据的过程是怎样

统计 vs 机器学习

统计	机器学习
Models Parameters Fitting, Estimate Regression/Classification Clustering,Density estimation	Network, Graph Weights Learning Supervised Learning Unsupervised Learning

随机试验

所有试验结果构成样本空间，随机事件是样本空间的子集

概率三大公理：

$P(E) in R, P(E)>=0, forall E in F$

$P(Omega)=1$

$P(U^infty _iE_i)=sum_{i=1}^infty P(E_i)$ $E_i$间互斥

随机变量

离散数据：PMF probability mass function 概率质量函数  $P(X=x)$

连续数据：PDF probability density function  概率密度函数  $f(x)=frac{dF(Xleq x)}{dx}$

CDF cumulative distribution function 累积分布函数(分布函数) $F(X<=x)$，是PDF的积分

多维随机变量

一次随机试验关注多个维度

联合分布：$P(Xleq x, Yleq y)$

边缘分布：$P(Xleq x)=sum P(Xleq x, Yleq +infty)$

条件分布：$P(Xleq x|Yleq y)=frac{P(Xleq x,Yleq y)}{P(Yleq y)}$

随机变量数字特征

• 众数：Mode，最可能出现的值
• 中位数：Mdedian，$P(Xgeq median)=P(Xleq mddian)=0.5$
• 期望：Expectation，反复抽样，期望得到的平均值

N阶矩：原点矩(c=0)&中心矩(c=期望)：$mu_n = int_{-infty}^{-infty}(x-c)^nf(x)dx$

归一化N阶中心矩 $frac{mu_n}{sigma^n}=frac{E[(X-mu)^n]}{sigma^n}$

N阶矩	原点矩	中心矩阵	归一化中心矩	表征(PDF)
1	期望			中心
2		方差		胖瘦
3			偏度	偏向skewness
4			峰度	尖锐度Kurtosis

• 方差

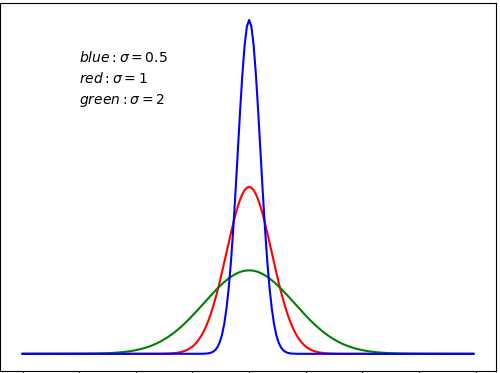
• 偏度

$gamma_1 = E[(frac{X-mu}{sigma})^3]=frac{mu_3}{sigma^3}=frac{E[(X-mu)^3]}{(E[(X-mu)^2])^{3/2}}=frac{kappa_3}{kappa_2^{3/2}}$

• 峰度

$Kurt[X] = E[(frac{X-mu}{sigma})^4]=frac{mu_4}{sigma^4}=frac{E[(X-mu)^4]}{(E[(X-mu)^2])^{2}}$

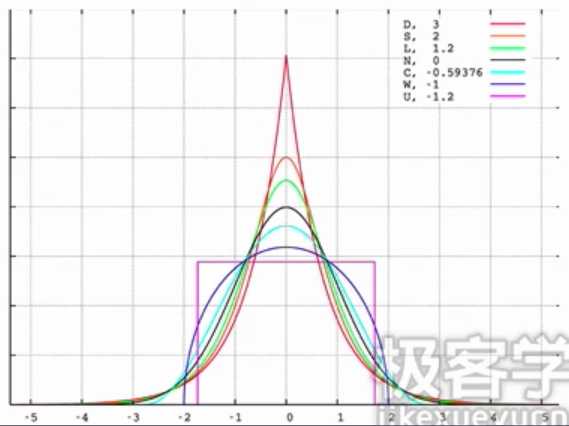
• 特征函数：频域变化，pdf的傅里叶变换

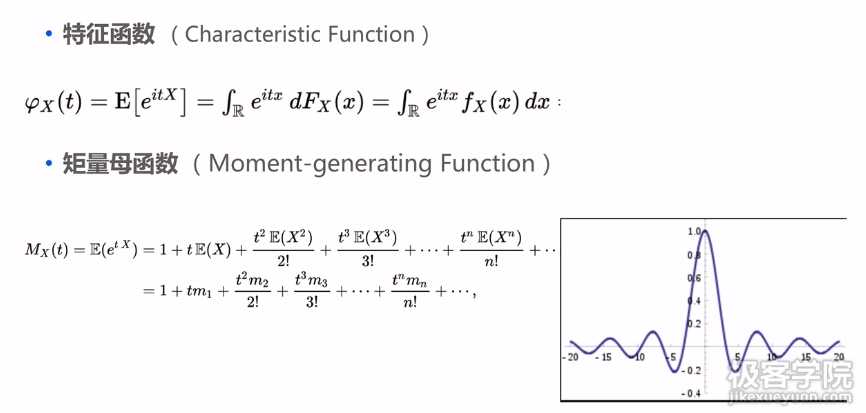
• 协方差：衡量两个变量的线性相关性

$Cov(X,Y)=E[(X-E[X])(Y-E[Y])]=E[XY]-E[X]E[Y]$

正相关：X越大，Y越大

负相关：X越大，Y越小

不相关：X和Y的变化没有关系

• 相关系数：标准化后的协方差

$ ho (X,Y)=frac{Cov(X,Y)}{sigma(X)sigma(Y)}$

• 余弦相似度：两个向量的相似度，余弦相似度玉相关系数的计算是一样的

$vec{X}=[(X_1-E[X])...(X_n-E[X])]$

$vec{Y}=[(Y_1-E[Y])...(Y_n-E[Y])]$

$r=frac{sum_{i=1}^n((X_i-E[X])(Y_i-E[Y]))}{sqrt{sum_{i=1}^n(X_i-E[X])^2}sqrt{sum_{i=1}^n(Y_i-E[y])^2}}$