置换群及其应用

Posted 2020-12-30 aininot260

置换群是由置换组成的群。即n元集合Ω到它自身的一个一一映射

称为Ω上的一个n元置换或n阶置换

Ω上的置换  可表示为

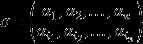
典型例题是POJ2369，给定一个序列,问需要最少需要置换多少次才能变为有序序列

有了这个定理就可以做题了，我们求出每一个数的最小循环节，求LCM就好了

介绍一下什么是循环节：

1 2 3 4 5

4 1 5 2 3

1->4->2->1

（1,4,2）为一个循环节，长度为3

 1 #include<cstdio>
 2 const int maxn=1005;
 3 int n;
 4 int a[maxn];
 5 int gcd(int a,int b)
 6 {
 7     return b==0?a:gcd(b,a%b);
 8 }
 9 int lcm(int a,int b)
10 {
11     return a/gcd(a,b)*b;
12 }
13 int main()
14 {
15     while(scanf("%d",&n)==1)
16     {
17         for(int i=1;i<=n;i++) scanf("%d",&a[i]);
18         int ans=1;
19         for(int i=1;i<=n;i++)
20         {
21             int tmp=a[i];
22             int cnt=1;
23             while(tmp!=i)
24             {
25                 tmp=a[tmp];
26                 cnt++;
27             }
28             ans=lcm(ans,cnt);
29         }
30         printf("%d",ans);
31     }
32     return 0;
33 }

超级超级简单的模拟