51nod1130-斯特林公式

Posted 2020-12-30 precious-zpf

题目链接：http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1130

斯特林公式能够近似的求出n的阶乘的值  然后我们再用  求位数公式  log10（n）+1就可以求出答案

斯特林公式   sqrt( 2*pi*n ) * pow( n/e , n)

斯特林公式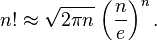          

而且  log10（）内的乘法 又可以转化为加法  那么我们就可以对斯特林公式优化为

    0.5 * log10( 2*PI*n ) + n*log10( n/e )

要注意   公式里用到了 e 和 派   我们定义他们有两种写法

#define PI acos(-1.0)
#define E exp(1.0)

const double e = 2.718281828459;
const double pi = 3.1415926535;

建议大家使用第一种  

尤其是这道题  数据特别的卡 刚开始 我定义e =2.71828182845； 疯狂的wa  wa了七八遍后  我又多加了一位e =2.718281828459  就对了。。。

所以  由于有的时候 我们不知道数据需要几位  用赋值的定义方式就可能出错

代码

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
#include<math.h>
using namespace std;
typedef long long ll;
#define PI acos(-1.0)
#define E exp(1.0)
const double e = 2.718281828459;
const double pi = 3.1415926535;
int T;
double n;
int main(){
    scanf("%d",&T);
    while(T--){
        scanf("%lf",&n);
        ll ans=(ll)(0.5*log10(2*PI*n) + n*(log10(n/E)) +1);
        printf("%I64d
",ans);
    }
    return 0;
}