BSGS（Baby-Step-Giant-Step）算法及其应用

Posted 2020-12-30 aininot260

先来稍微回顾一下，我们已经会求模线性方程（包括其特殊情况乘法逆元）

我们还会进行幂取模的快速算法（模是质数用费马小定理，模一般情况用欧拉定理）

对于幂中指数特别大的情况，我们还延伸出了拓展欧拉定理来解决

对于模线性方程组来说，模数互质的时候直接用孙子定理

模数不互质的时候用方程合并的思想，引申出拓展中国剩余定理

接下来要学的这个东西可以说也是解模方程的，只不过是超越方程

咋超越的呢？

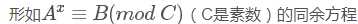
方法不容变通，直接抄过来

转自https://blog.csdn.net/zzkksunboy/article/details/73162229

典型例题是POJ2417，就是求这个东西

要求一个最小整数解

脑子不够用了QAQ睡眠QAQ

 1 #include<cmath>
 2 #include<cstdio>
 3 #include<algorithm>
 4 using namespace std;
 5 struct Hashmap
 6 {
 7     static const int Ha=999917,maxe=46340;
 8     int E,lnk[Ha],son[maxe+5],nxt[maxe+5],w[maxe+5];
 9     int top,stk[maxe+5];
10     void clear(){E=0;while(top) lnk[stk[top--]]=0;}
11     void Add(int x,int y){son[++E]=y;nxt[E]=lnk[x];w[E]=0x7fffffff;lnk[x]=E;}
12     bool count(int y)
13     {
14         int x=y%Ha;
15         for(int j=lnk[x];j;j=nxt[j])
16             if(y==son[j]) return true;
17         return false;
18     }
19     int& operator [](int y)
20     {
21         int x=y%Ha;
22         for(int j=lnk[x];j;j=nxt[j])
23             if(y==son[j]) return w[j];
24         Add(x,y);stk[++top]=x;return w[E];    
25     }
26 }f;
27 int exgcd(int a,int b,int &x,int &y)
28 {
29     if(b==0) {x=1;y=0;return a;}
30     int r=exgcd(b,a%b,x,y);
31     int t=x;x=y;y=t-a/b*y;
32     return r;
33 }
34 int BSGS(int A,int B,int C)
35 {
36     if(C==1) if(B==0) return A!=1;else return -1;
37     if(B==1) if(A!=0) return 0;else return -1;
38     if(A%C==0) if(B==0) return 1;else return -1;
39     int m=ceil(sqrt(C)),D=1,Base=1;f.clear();
40     for(int i=0;i<=m-1;i++)
41     {
42         f[Base]=min(f[Base],i);
43         Base=((long long)Base*A)%C;
44     }
45     for(int i=0;i<=m-1;i++)
46     {
47         int x,y,r=exgcd(D,C,x,y);
48         x=((long long)x*B%C+C)%C;
49         if(f.count(x)) return i*m+f[x];
50         D=((long long)D*Base)%C;
51     }
52     return -1;
53 }
54 int main()
55 {
56     int A,B,C;
57     while(scanf("%d%d%d",&C,&A,&B)==3)
58     {
59         int ans=BSGS(A,B,C);
60         if(ans==-1) printf("no solution
");
61         else printf("%d
",ans);
62     }
63     return 0;
64 }