前缀和，二维前缀和！

Posted 2020-12-30 lyfoi

前缀和

定义

用空间换取效率，做一个预处理，然后可以(O(1))的查询某个区间的值的和。

实现

设(s_i)为第(i)个数(a_i)的前缀和，则(s_i=s_i-1+a_i)

当要查找区间的和时只要把对应的起点终点的元素相减即可。

例题

Educational Codeforces Round 30B Balanced Substring

翻译

给你一个长度至多为(100000)的(01)串，其中含有相同(0)，(1)个数的子串被称为“平衡串”，问你最长的平衡串的长度。

思路

第一直觉是暴力，第二直觉看到数据范围不可行，第三直觉是绝望，第四直觉是前缀和。

一道前缀和的题目，遇到(1)就加(1)，遇到(0)就减(1)。如果某个终点减去某个起点的值为(0)，那么就记录并且选择最大的答案。不过有个问题就是起点和终点使用双层循环枚举会妥妥的(TLE)，于是考虑使用(map)标记起点。

Code

#include<bits/stdc++.h>
using namespace std;
map<int,int> mp;
char s[100001];
int main()
{
    int n;
    cin>>n;
    cin>>s+1; 
    int ans=0,sum=0;
    mp[0]=0;
    for (int i=1; i<=n;i++)
    {
        if (s[i]=='1')sum++; 
        else sum--;
        if (mp.find(sum)==mp.end())
            mp[sum]=i;
        else 
            ans=max(ans,i-mp[sum]);
    }
    cout<<ans<<endl;
    return 0;
}

二维前缀和

定义

基本和普通的前缀和差不多，不过二维前缀和是给你一个矩阵的一部分（右上角和左下角），让你查询这一部分的元素的和。

实现

如果直接暴力枚举，那么效率低低下。所以宝宝总结了一个公式：

(x)减，(y)减，(xy)都减。（记录）

不减，都减，减混合减。（查询）

正常描述就是：

首先预处理处以所有点为右下角,((1,1))为左上角的矩阵中的元素和（记录）。

接着((x1,y1))为右下角,((x2,y2))为左上角的矩形中的元素和为：

(f_{x_1y_1}+f_{x_2-1 y_2-1}-f_{x_1y_2-1}-f_{x_2-1y_1})

例题

前方高能！(AGC)的(C)题！

AGC 15 C Nuske vs Phantom Thnook

翻译

(Nuske) 现在有一个 (N*M(N,M<=2000)) 的矩阵 (S) , 若 (S_i,j=1) , 那么该处为蓝色, 否则为白色, 保证所有蓝色格子之间只有一条路。

给出 (Q(Q<=200000)) 次询问, 每次询问你一个子矩阵中蓝色连通块的个数 。

思路

大水题，我深度优先搜索判断联通块就完事了，然鹅一看数据，顿时倒地不起（救命！）。

回归正题，仔细一瞅发现一个奇怪的地方：保证所有蓝色格子之间只有一条路。也就是说，所有的联通块都是一棵树。这就见鬼了，树跟联通块有半毛钱关系啊！

按照大神的套路（宝宝你肯定看题解了对不对？）来做一下。

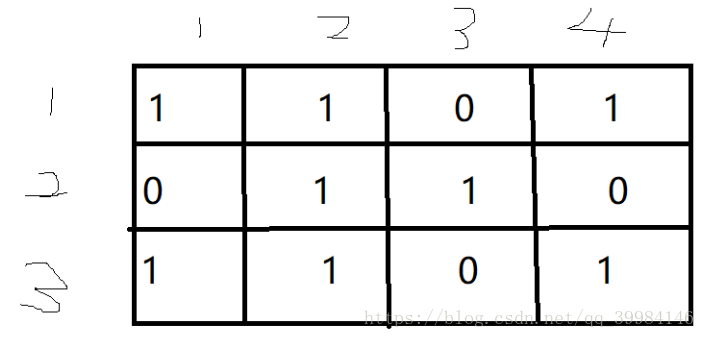
下面是样例一的图（太丑了(233)）：

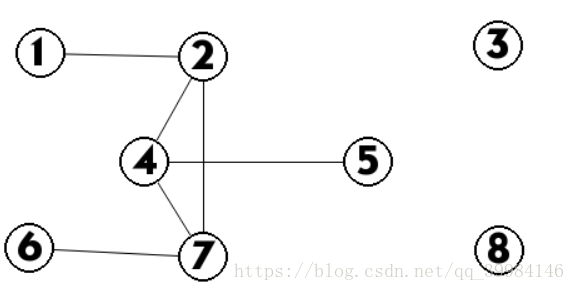
以第一个询问为例子，我们把所有的蓝点(1)连成树（相邻的两个(1)连边）。

发现联通块的数量(=)点的数量(-)边的数量，于是这道题变成了：给你一个(01)矩阵，求这个矩阵的一个子矩阵中的(1)的数量-连续两个(1)的数量。

由于数据范围死大，于是二维前缀和。对于连续两个(1)就可以发现一个1在向它周围判断即可

Code

#include<bits/stdc++.h>
using namespace std;
int n,m,q;
int f[2001][2001],h[2001][2001],g[2001][2001];
char s[2001][2001];
int main()
{
    cin>>n>>m>>q;
    for(int i=1; i<=n; i++)
        cin>>s[i]+1;
    memset(f,0,sizeof(f));
    memset(h,0,sizeof(h));
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
        {
            f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+(s[i][j]-'0');
            h[i][j]=h[i-1][j]+h[i][j-1]-h[i-1][j-1];
            g[i][j]=g[i-1][j]+g[i][j-1]-g[i-1][j-1];
            if(s[i][j]=='1')
            {
                if(s[i][j-1]=='1') h[i][j]++;
                if(s[i-1][j]=='1') g[i][j]++;
            }
        }
    while(q--)
    {
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        int k1=f[x2][y2]-f[x2][y1-1]-f[x1-1][y2]+f[x1-1][y1-1];
        int k2=h[x2][y2]-h[x2][y1]-h[x1-1][y2]+h[x1-1][y1];
        int k3=g[x2][y2]-g[x1][y2]-g[x2][y1-1]+g[x1][y1-1];
        cout<<k1-k2-k3<<endl;
    }
    return 0;
}