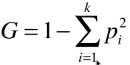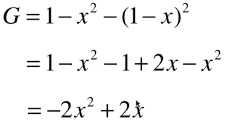机器学习：决策树（基尼系数）

Posted 2020-12-29 volcao

一、基础理解

　1）公式

• 

1. k：数据集中样本类型数量；
2. P_i：第 i 类样本的数量占总样本数量的比例

 

　2）实例计算基尼系数

• 3 种情况计算基尼系数：
• 
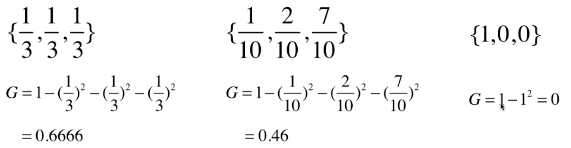
• 基尼系数的性质与信息熵一样：度量随机变量的不确定度的大小；

1. G 越大，数据的不确定性越高；
2. G 越小，数据的不确定性越低；
3. G = 0，数据集中的所有样本都是同一类别；

 

　3）只有两种类别的数据集

• 

1. x：两类样本中，其中一类样本数量所占全部样本的比例；
2. 当 x = 0.5，两类样本数量相等时，数据集的确定性最低；

 

 

二、使用基尼系数划分节点数据集

　1）格式

• from sklearn.tree import DecisionTreeClassifier
  
  dt_clf = DecisionTreeClassifier(max_depth=2, criterion=‘gini‘)
  dt_clf.fit(X, y)

1. criterion=‘gini‘：使用 “基尼系数” 方式划分节点数据集；

2. criterion=‘entropy‘：使用 “信息熵” 方式划分节点数据集；

 

　2）代码实现

• 导入数据集

  import numpy as np
  import matplotlib.pyplot as plt
  from sklearn import datasets
  
  iris = datasets.load_iris()
  X = iris.data
  y = iris.target

   

• 封装函数：

1. split()：划分数据集；
2. gini()：计算数据集的基尼系数；
3. try_split()：寻找最佳的特征、特征值、基尼系数；

   from collections import Counter
   from math import log
   
   def split(X, y, d, value):
       index_a = (X[:, d] <= value)
       index_b = (X[:, d] > value)
       return X[index_a], X[index_b], y[index_a], y[index_b]
   
   def gini(y):
       counter = Counter(y)
       res = 1.0
       for num in counter.values():
           p = num / len(y)
           res += -p**2
       return res
   
   def try_split(X, y):
       
       best_g = float(‘inf‘)
       best_d, best_v = -1, -1
       for d in range(X.shape[1]):
           sorted_index = np.argsort(X[:,d])
           for i in range(1, len(X)):
               if X[sorted_index[i-1], d] != X[sorted_index[i], d]:
                   v = (X[sorted_index[i-1], d] + X[sorted_index[i], d]) / 2
                   x_l, x_r, y_l, y_r = split(X, y, d, v)
                   g = gini(y_l) + gini(y_r)
                   if g < best_g:
                       best_g, best_d, best_v = g, d, v
                       
       return best_g, best_d, best_v

    

• 第一次划分

  best_g, best_d, best_v = try_split(X, y)
  X1_l, X1_r, y1_l, y1_r = split(X, y, best_d, best_v)
  
  gini(y1_l)
  # 数据集 X1_l 的基尼系数：0.0
  
  gini(y1_r)
  # 数据集 X1_r 的基尼系数：0.5

  # 判断：数据集 X1_l 的基尼系数等于 0，不需要再进行划分,；数据集 X1_r 需要再次进行划分；

 

• 第二次划分

  best_g2, best_d2, best_v2 = try_split(X1_r, y1_r)
  X2_l, X2_r, y2_l, y2_r = split(X1_r, y1_r, best_d2, best_v2)
  
  gini(y2_l)
  # 数据集 X2_l 的基尼系数：0.1680384087791495
  
  gini(y2_r)
  # 数据集 X2_l 的基尼系数：0.04253308128544431

  # 判断：数据集 X2_l 和 X2_r 的基尼系数不为 0，都需要再次进行划分；

 

 

三、信息熵  VS  基尼系数

• 信息熵的计算比基尼系数慢

1. 原因：计算信息熵 H 时，需要计算一个 log(P)，而基尼系数只需要计算 P²；
2. 因此，scikit-learn 中的  DecisionTreeClassifier()  类中，参数  criterion = ‘gini‘，默认选择基尼系数的方式进行划分节点数据集；

• 大多数时候，二者没有特别的效果优劣；