欧拉筛法（线性筛法）与解积性函数

Posted 2020-12-29 zhy-ak

日常吐槽：啧啧啧今天真是玄幻的一天。早上睡到9:10发现睡过了一个半小时，在9:30狂奔来机房 + 吃早餐，最后只剩一个半小时心态崩—>光荣爆零？？？又在下午四点把全部题改完？？？上午和下午的效率真的不是一个级别的啊...好的接下来把这道奇葩例题。

JZOJ 4732 函数

 

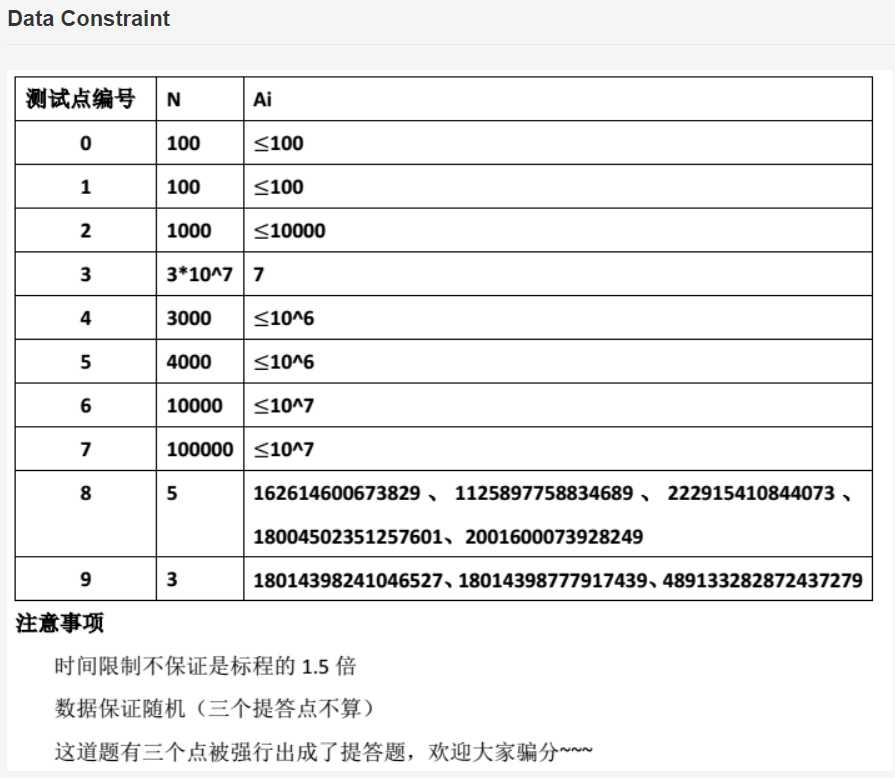
题解

　　23333这真的是出题人中的一股清流了，对建议打表的那三个点先表示感激（虽然我还是爆零因为压根儿没看懂题目）

　　让我们大胆地猜测一下，这个不知道是什么鬼玩意儿的函数是什么东西呢？好，拿起笔和草稿纸，模拟，没错！就！是！欧！拉！函！数！

　　真是人生处处充满惊喜啊，20分到手。

　　还想再高一点，没问题，直接加上个欧拉筛，你已拥有50分。

　　OKOK，你可以再用欧拉函数的积性函数特性，70分啦。

　　打表的三个点最为玄学，参见下图。

　　

 

　　　　完美，接下来我们要做的就是AC了

代码

　

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n, tot = 0;
int prime[(int)1e7 + 1], phi[(int)1e7 + 1];
int main()
{
    scanf("%d", &n);
    if (n == (int)1e7 * 3) 
    {
        printf("%lld
", (long long)1e7 * 18);
        return 0;
    }
    if (n == 3)
    {
        printf("525162079891401242
");
        return 0;
    }
    if (n == 5)
    {
        printf("21517525747423580
");
        return 0;
    }
    phi[1] = 1;
    for (int i = 2; i <= 1e7; i++)
    {
        if (!phi[i])
        {
            prime[++tot] = i;
            phi[i] = i - 1;
        }
        for (int j = 1; j <= tot; j++)
        {
            if (i * prime[j] > 1e7) break;
            if (i % prime[j] != 0)
                phi[i * prime[j]] = phi[i] * phi[prime[j]];
            else
            {
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }
        }
    }
    long long ans = 0;
    for (int i = 1; i <= n; i++)
    {
        int a;
        scanf("%d", &a);
        ans += phi[a];
    }
    printf("%lld", ans);
    return 0;
}

 

　　23333全场最快不解释，先嘚瑟一会儿（真的没有故意卡！）

　　顺便贴两个很好的博客文章，

　　https://www.cnblogs.com/grubbyskyer/p/3852421.html

　　https://blog.csdn.net/y20070316/article/details/51729812