poj-1021--2D-Nim--点阵图同构

Posted 2020-12-29 fantastic123

2D-Nim

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 4136		Accepted: 1882

Description

The 2D-Nim board game is played on a grid, with pieces on the grid points. On each move, a player may remove any positive number of contiguous pieces in any row or column. The player who removes the last piece wins. For example, consider the left grid in the following figure. 
 
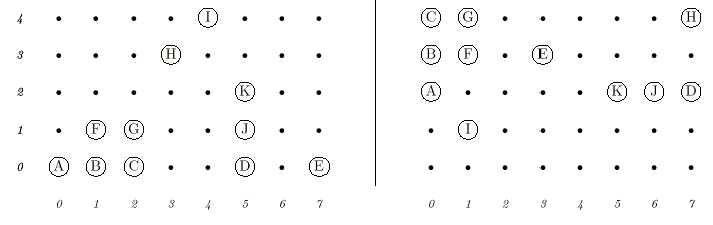
The player on move may remove (A), (B), (A, B), (A, B, C), or (B,F), etc., but may not remove (A, C), (D, E), (H, I) or (B, G). 
For purposes of writing 2D-Nim-playing software, a certain programmer wants to be able to tell whether or not a certain position has ever been analyzed previously. Because of the rules of 2D-Nim, it should be clear that the two boards above are essentially equivalent. That is, if there is a winning strategy for the left board, the same one must apply to the right board. The fact that the contiguous groups of pieces appear in different places and orientations is clearly irrelevant. All that matters is that the same clusters of pieces (a cluster being a set of contiguous pieces that can be reached from each other by a sequence of one-square vertical or horizontal moves) appear in each. For example, the cluster of pieces (A, B, C, F, G) appears on both boards, but it has been reflected (swapping left and right), rotated, and moved. Your task is to determine whether two given board states are equivalent in this sense or not.

Input

The first line of the input file contains a single integer t (1 ≤ t ≤ 10), the number of test cases, followed by the input data for each test case. The first line of each test case consists of three integers W, H, and n (1 ≤ W, H ≤ 100). W is the width, and H is the height of the grid in terms of the number of grid points. n is the number of pieces on each board. The second line of each test case contains a sequence of n pairs of integers xi , yi, giving the coordinates of the pieces on the first board (0 ≤ xi < W and 0 ≤ yi < H). The third line of the test case describes the coordinates of the pieces on the second board in the same format.

Output

Your program should produce a single line for each test case containing a word YES or NO indicating whether the two boards are equivalent or not.

Sample Input

2
8 5 11
0 0 1 0 2 0 5 0 7 0 1 1 2 1 5 1 3 3 5 2 4 4
0 4 0 3 0 2 1 1 1 4 1 3 3 3 5 2 6 2 7 2 7 4
8 5 11
0 0 1 0 2 0 5 0 7 0 1 1 2 1 5 1 3 3 6 1 4 4
0 4 0 3 0 2 1 1 1 4 1 3 3 3 5 2 6 2 7 2 7 4

Sample Output

YES
NO

总结

就是连通性和图的同构判断。

分析

找出属于同一组的点很简单，DFS就可以搞定。图的同构可以用图的Hash来判断。这个不是我想出来的，是网上看来的：
∑i,]distance(pi,pj)∑i,]distance(pi,pj)
即同一组中所有点的距离加起来，这个数值做为这个图的哈希值。

 

/*
    author:tonygsw
    data:2018.8.7
    account:zj1228
    link:http://poj.org/problem?id=1020
*/
#define ll long long
#define IO ios::sync_with_stdio(false)

#include<map>
#include<queue>
#include<math.h>
#include<vector>
#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
using namespace std;
class Node{
    public:
        int x,y;
};
Node node[10005];int hash1[10005],hash2[1005];
int matri[105][105];bool vis[105][105];
int w,h,num,len,len1,len2;int to[4][2]={1,0,-1,0,0,1,0,-1};
void init()
{
    memset(matri,0,sizeof(matri));
    memset(vis,0,sizeof(vis));
    len1=len2=0;
}
bool judge(int x,int y)
{
    if(x>=0&&x<w&&y>=0&&y<h&&matri[x][y]&&(!vis[x][y]))
        return true;
    return false;
}
int dis(Node a,Node b)
{
    return pow(a.x-b.x,2)+pow(a.y-b.y,2);
}
void bfs(int x,int y,int ju)
{
    Node beg,nex;len=0;
    queue<Node>way;
    beg.x=x,beg.y=y;
    way.push(beg);
    vis[x][y]=1;
    node[len++]=beg;
    while(!way.empty())
    {
        beg=way.front();
        way.pop();
        for(int i=0;i<4;i++)
        {
            nex.x=beg.x+to[i][0];
            nex.y=beg.y+to[i][1];
            if(judge(nex.x,nex.y))
            {
                way.push(nex);
                vis[nex.x][nex.y]=1;
                node[len++]=nex;
            }
        }
    }
    for(int i=0;i<len;i++)
        for(int j=0;j<len;j++)
        {
            if(ju)hash1[len1++]=dis(node[i],node[j]);
            else hash2[len2++]=dis(node[i],node[j]);
        }
}
bool ans()
{
    if(len1!=len2)return false;
    else
    {
        sort(hash1,hash1+len1);
        sort(hash2,hash2+len2);
        for(int i=0;i<len1;i++)
        {
            if(hash1[i]!=hash2[i])return false;
        }
        return true;
    }
}
int main()
{
    int t;
    scanf("%d",&t);int x,y;
    while(t--)
    {
        init();
        scanf("%d%d%d",&w,&h,&num);
        for(int i=0;i<num;i++)
        {
            scanf("%d%d",&x,&y);
            matri[x][y]=1;
        }
        for(int i=0;i<w;i++)
            for(int j=0;j<h;j++)
                if(matri[i][j]&&(!vis[i][j]))
                    bfs(i,j,1);
        memset(matri,0,sizeof(matri));
        memset(vis,0,sizeof(vis));
        for(int i=0;i<num;i++)
        {
            scanf("%d%d",&x,&y);
            matri[x][y]=1;
        }
        for(int i=0;i<w;i++)
            for(int j=0;j<h;j++)
                if(matri[i][j]&&(!vis[i][j]))
                    bfs(i,j,0);

        if(ans())cout<<"YES"<<endl;
        else cout<<"NO"<<endl;
    }
    return 0;
}
/*
2
8 5 11
0 0 1 0 2 0 5 0 7 0 1 1 2 1 5 1 3 3 5 2 4 4
0 4 0 3 0 2 1 1 1 4 1 3 3 3 5 2 6 2 7 2 7 4
8 5 11
0 0 1 0 2 0 5 0 7 0 1 1 2 1 5 1 3 3 6 1 4 4
0 4 0 3 0 2 1 1 1 4 1 3 3 3 5 2 6 2 7 2 7 4
*/