集训(camp)

Posted 2020-12-29 iamqzh233

题目描述

小海在真姬家附近举办了一次集训。真姬家附近是一片沙滩，可以看做n x m的方格，有些方格内有别墅，一个方格和它上下左右四个方格相邻。

     小海打算进行k次训练，为了方便每次训练会在两栋相邻的别墅之间，且不会有两次训练地点相同。但训练会打扰居民。若任意两次训练的地点在同一栋别墅附近，会令这里的居民不满。如果这两个地点与别墅组成L字，会产生A点不满；如果这两个地点与别墅在一条线上，会产生B点不满。

     小海想要知道进行任意次集训最少会产生多少不满。

输入

第一行1个正整数t表示测试点编号（所有样例的编号均为0，样例均不满足任何特殊性质）。

第二行4个正整数n,m,A,B。

接下来n行，其中第i行一个长度为m的字符串Si,[1,m] ，S_{i,j}表示网格的第i行第j列，‘0’表示存在别墅，‘1’表示不存在别墅。

接下来一行1个正整数q。

输出

输出q行，第i行为k=i时的答案。

样例输入

0
2 4 20 50
0001
0001
7

样例输出

0
0
0
40
80
170
260

提示

 样例k=6的方案：

 

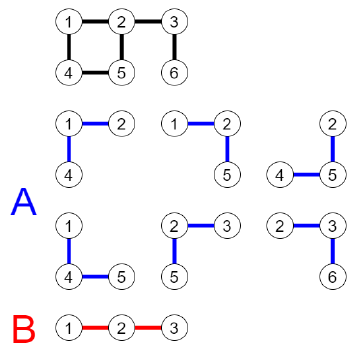
数据范围：

一共25个测试点

1-7测试点 n,m<=8

8-12测试点 若答案>0输出1

13-19测试点 A=B

 

费用流。

对整个图，按照横坐标加纵坐标的奇偶性分为两部分，一部分是白点，一部分是黑点

如果A=B，我们可以直接对于S到白点连四条边，费用依次为0,A,2A,3A，黑点连向T。

再把相邻的连边就可以了，意思也就是说不满程度只与一个点有选了几个与其相邻的点有关。

对于A<=B，我们就是要把一些算成$L$字贡献的改成直线的贡献，也就是加上B-A

那么这时候对于一个点，我们要知道上面和下面加起来用了几次，如果是两次就是B-A，一次就是0

左右也是同理的。

那么我们可以对于每一个别墅，多建两个点，表示上下和左右。

别墅像上下连一条费用为0的边，再连一条费用是B-A的边。左右同理。

那么相邻的点就只要连接左右或者上下的点就可以了。

注意。。有个部分分是答案大于0就输出1。

  1 #pragma GCC optimize(2)
  2 #include <bits/stdc++.h>
  3 using namespace std;
  4 #define M 200010
  5 #define inf 1047483647
  6 int n, m, A, B;
  7 char str[50][50];
  8 int s, t;
  9 struct Edge{
 10     int u, v, cap, flow, cost, Next;
 11 } G[M];
 12 int head[M], tot;
 13 int d[M], inq[M], p[M], a[M];
 14 inline void init() {
 15     memset(head, -1, sizeof(head));
 16     tot = -1;
 17 }
 18 inline void add(int u, int v, int w, int cost) {
 19     G[++ tot] = (Edge){u, v, w, 0, cost, head[u]};
 20     head[u] = tot;
 21     G[++ tot] = (Edge){v, u, 0, 0, -cost, head[v]};
 22     head[v] = tot;
 23 }
 24 inline bool Do(int &flow, int &cost) {
 25     for(int i = s; i <= t; ++ i) d[i] = inf;
 26     for(int i = s; i <= t; ++ i) inq[i] = 0;
 27     d[s] = 0; inq[s] = 1;
 28     p[s] = 0; a[s] = inf;
 29     queue<int> Q;
 30     Q.push(s);
 31     while(!Q.empty()) {
 32         int u = Q.front(); Q.pop();
 33         inq[u] = 0;
 34         for(int i = head[u]; i != -1; i = G[i].Next) {
 35             Edge& e = G[i];
 36             if(e.cap > e.flow && d[e.v] > d[u] + e.cost) {
 37                 d[e.v] = d[u] + e.cost;
 38                 p[e.v] = i;
 39                 a[e.v] = min(a[u], e.cap - e.flow);
 40                 if(!inq[e.v]) {
 41                     Q.push(e.v);
 42                     inq[e.v] = 1;
 43                 }
 44             }
 45         }
 46     }
 47     if(d[t] == inf) return false;
 48     ++ flow;
 49     cost += d[t];
 50     int u = t;
 51     while(u != s) {
 52         G[p[u]].flow ++;
 53         G[p[u] ^ 1].flow --;
 54         u = G[p[u]].u;
 55     }
 56     return true;
 57 }
 58 int id[50][50];
 59 int main() {
 60     int T;
 61     scanf("%d%d%d%d%d", &T, &n, &m, &A, &B);
 62     for(int i = 1; i <= n; ++ i) {
 63         scanf("%s", str[i] + 1);
 64     }
 65     init();
 66     int cnt = 0;
 67     for(int i = 1; i <= n; ++ i) {
 68         for(int j = 1; j <= m; ++ j) {
 69             if(str[i][j] == ‘0‘) {
 70                 id[i][j] = ++ cnt;
 71             }
 72         }
 73     }
 74     s = 0, t = cnt * 3 + 1;
 75     for(int i = 1; i <= n; ++ i) {
 76         for(int j = 1; j <= m; ++ j) if(id[i][j]) {
 77             if(i + j & 1) {
 78                 add(s, id[i][j], 1, 0);
 79                 add(s, id[i][j], 1, A);
 80                 add(s, id[i][j], 1, 2 * A);
 81                 add(s, id[i][j], 1, 3 * A);
 82                 add(id[i][j], id[i][j] + cnt, 1, 0);
 83                 add(id[i][j], id[i][j] + cnt, 1, B - A);
 84                 add(id[i][j], id[i][j] + 2 * cnt, 1, 0);
 85                 add(id[i][j], id[i][j] + 2 * cnt, 1, B - A);
 86                 if(id[i - 1][j]) {
 87                     add(id[i][j] + cnt, id[i - 1][j] + cnt, 1, 0);
 88                 }
 89                 if(id[i + 1][j]) {
 90                     add(id[i][j] + cnt, id[i + 1][j] + cnt, 1, 0);
 91                 }
 92                 if(id[i][j - 1]) {
 93                     add(id[i][j] + 2 * cnt, id[i][j - 1] + 2 * cnt, 1, 0);
 94                 }
 95                 if(id[i][j + 1]) {
 96                     add(id[i][j] + 2 * cnt, id[i][j + 1] + 2 * cnt, 1, 0);
 97                 }
 98             }
 99             else {
100                 add(id[i][j], t, 1, 0);
101                 add(id[i][j], t, 1, A);
102                 add(id[i][j], t, 1, 2 * A);
103                 add(id[i][j], t, 1, 3 * A);
104                 add(id[i][j] + cnt, id[i][j], 1, 0);
105                 add(id[i][j] + cnt, id[i][j], 1, B - A);
106                 add(id[i][j] + 2 * cnt, id[i][j], 1, 0);
107                 add(id[i][j] + 2 * cnt, id[i][j], 1, B - A);
108             }
109         }
110     }
111     int q;
112     scanf("%d", &q);
113     int flow = 0, cost = 0;
114     while(q --) {
115         Do(flow, cost);
116         if(8 <= T && T <= 12) {
117             if(cost) puts("1");
118             else puts("0");
119         }
120         else printf("%d
", cost);
121     }
122 }