图的存储：链式前向星（边集数组）

Posted 2020-12-29 liyian

申明：本文中提及的所有存图结构都用静态数组实现，而非链表。

0.什么是链式前向星

　　链式前向星是一种存图的结构，例如前向星、邻接矩阵、边表、邻接表等也是存图的结构。

1.链式前向星有何优点

　　链式前向星：空间利用率高，在各类竞赛中常被使用。

　　邻接矩阵：需要开N*N的空间，在各类竞赛中常被卡。

　　邻接表：空间复杂度略小于邻接矩阵，但会被极端数据卡爆，且无法记录权值。

　　边表：无法迅速判断两点连通性，以至不适用于大多数图的算法。

　　前向星：具有排序操作，时间复杂度高。

2.同类结构介绍

　　邻接矩阵：开二维数组，第一维表示起点，第二维表示终点。

　　　　举例：a[i][j]的值表示第i个点与第j个点是否联通（0/1）。

　　邻接表：开二维数组，第一维表示起点，第二维存储终点。

　　　　举例：a[i][j]的值表示第i个点所连接的第j个点的序号，其中a[i][0]表示第i个点所连接的点的数量。

　　边表：纯粹存储边的信息，开一维数组，用结构体存储，结构体包含这条边的三条信息，即起点终点和权值。

　　　　举例：a[i]存储了第i条边的信息，其中a[i].s表示起点a[i].e表示终点a[i].w表示权值。

　　前向星：可以理解为边表的改进，对边表中的元素按照起点为第一关键字排序，终点为第二关键字进行排序。

　　　　不举例子了

3.链式前向星如何实现。

　　个人推荐使用如下三个数组：head[N]、next[M]、end[M]

　　head[i]存以i为起点的第一条边,next[i]表示与第i条边同起点的下一条边，end[i]表示第i条边的终点。

　　其中next数组与end数组对齐。

　　如何建图呢？

int num=0;
for (int i=1;i<=m;i++)
{
    cin>>x>>y;
    next[++num]=head[x];
    head[x]=num;
    end[num]=y;
    next[++num]=head[y];
    head[y]=num;end[num]=x;
}//因为建双向边所以写了两遍

 

 

 

　　举例：

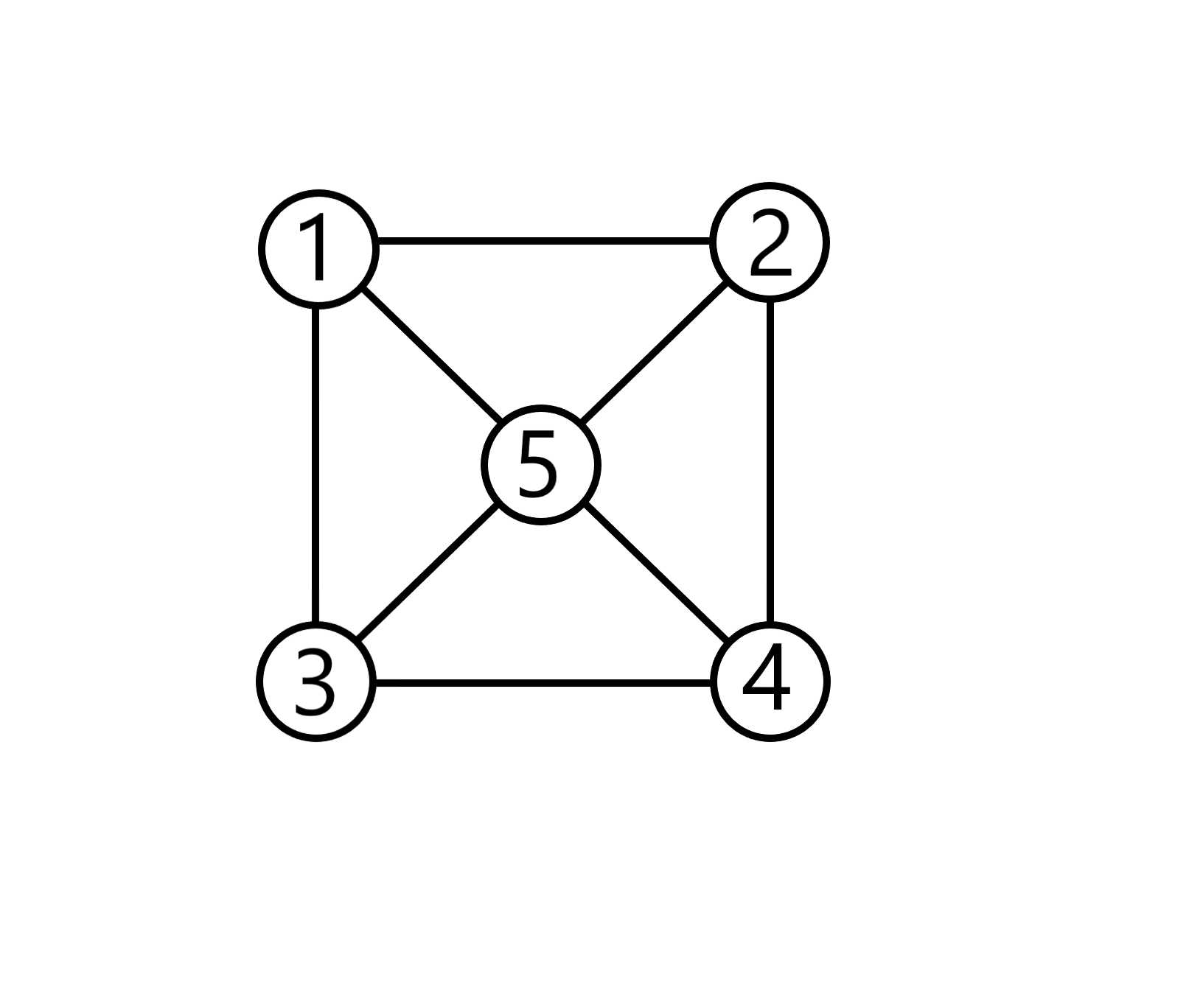
　　那么输入数据一目了然：5 8　　1 2　　1 3　　1 5　　2 4　　2 5　　3 4　　3 5　　4 5

　　那么程序运行完几个数组是什么样子呢？

 

 

head	5	9	13	15	16
next	0	0	1	0	3	0	2	0	7	6	4	8	11	10	12	14
end	2	1	3	1	5	1	4	2	5	2	4	3	5	3	5	4

　　注意看其中标注为红色的部分，head[5]的值为16，表示5所连接的第一个点在下标为16的end数组中（end[16]=4表示5所连接的第一个点是4）。

　　那么我们只知道第一个点，怎么知道最后一个点呢？用next数组实现。

　　next[16]=14，表示5所连接的第二个点在在下标为14的end数组中，而next[14]=10,说明第三个点下标为10，这样循环指向，直到最后指向next[6]=0，说明下标为end[6]是最后一个点。

　　那么如何实现对5所连接的点的穷举呢？

　　

1 //第一种
2 for (int k=head[x];k>0;k=next[k])
3     cout<<end[k]<<endl;
4 //第二种
5 int k=head[x];
6 while (k>0){
7     cout<<end[k]<<endl;
8     k=next[k];
9 }

　　这里只讲了链式前向星的大概含义和使用方法，更加详细的原理以及其在算法内的运用会在我的下一篇随笔中讲解。