树状数组及二维树状数组

Posted 2020-12-29 ifmyt

一直以为树状数组能用线段树水过去，直到我今天碰上了树状数组模板题。

然后就是开始认真的学习树状数组，突然发现怎么这么好写qwqqqq。

部分内容转自https://www.cnblogs.com/hsd-/p/6139376.html

一.树状数组

树状数组是一种数据结构，核心思想是利用二进制的补码思想。

首先就是树状数组的结构图

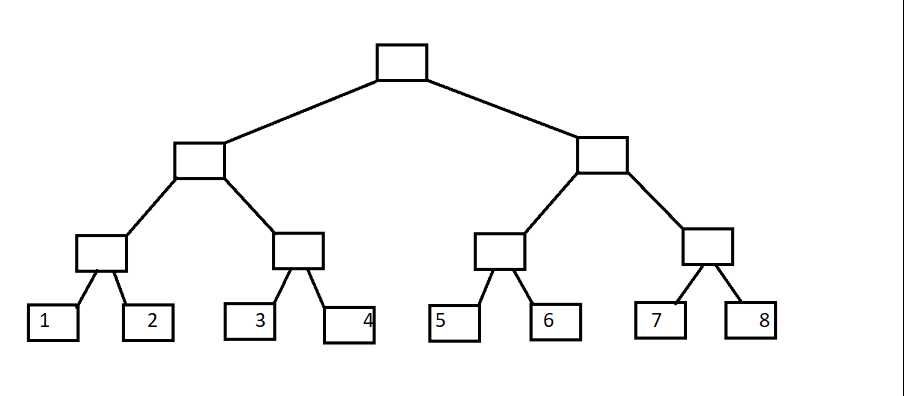
然后我们对他进行变形

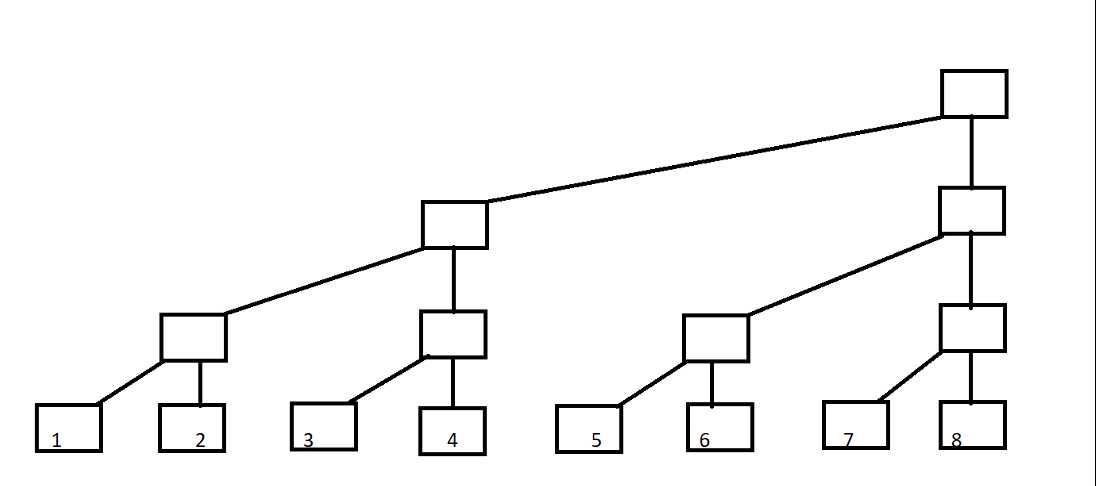
是不是感觉更好理解了呢？

然后我们对其进行标号

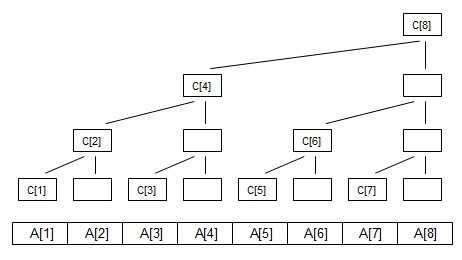
c数组表示的是记录的值，A数组表示的是原序列。然后就是所有关于树状数组的博客都会有的c数组的存值的展示，博主较懒就不写了，具体看推荐博客。

最重要的性质是

C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; （k为i的二进制中从最低位到高位连续零的长度）

上面说k是二进制中最低位到最高位的连续零的长度也就是6的二进制是110，那么k就是1，然后我们带入:

c[6]=A[6-2+1]+A[6-2+2]=A[5]+A[6]

看，是不是与上方式子相符，这就是lowbit要实现的功能。那么，lowbit实现的原理是啥呢？

先粘一下lowbit函数的代码

1 int lowbit(int k)
2 {
3     return k&(-k);
4 }

lowbit

k&(-k)是啥意思呢？

-k是k的补码，也就是反码+1，反码是啥自行百度，反正也很简单。

然后你就会发现，你能够取出最小一位的1，而在上面的例子中就是2，你可以再用几组数据试一下，发现lowbit(i)=2^i。

4(0100)，反码4(0011)，补码(0100)，0100&0100=0100,则lowbit(i)=4，又根据连续0的位数，则k=2，2^2=4，则假设成立。

所以，是不是非常的明白了？

其实还有一种lowbit的写法，k&(k^(k-1))，可以自己手推一下。

然后就是单点修改，代码

1 void add(int x,int val)
2 {
3     while(x<=n)
4     {
5         tree[x]+=val;
6         x+=lowbit(x);
7     }
8 }

单点修改

为啥是i<=n呢？因为你单点修改是要从叶子结点蹦向父节点的，所以要从小到大。

 1 int sum(int x)
 2 {
 3     int ans=0;
 4     while(x>0)
 5     {
 6         ans+=tree[x];
 7         x-=lowbit(x);
 8     }
 9     return ans;
10 }

区间查询

那为啥区间查询是i!=0呢？因为区间查询是从父节点蹦向子节点的，所以i要不断减小，记住区间查询是查询的前缀和，所以要查[l,r]的话需要sum(r)-sum(l-1)。

会了以上操作，就先做一下模板题吧 P3374 【模板】树状数组 1、

如果我们想区间修改呢？你该不会是枚举然后add（i）吧，不T才怪啊！

这时我们就用到了一种新的思想，差分思想。差分思想是很常见的，下面介绍一下：

数组a[]={1,6,8,5,10}，那么差分数组b[]={1,5,2,-3,5}

也就是说b[i]=a[i]-a[i-1];(a[0]=0;)，那么a[i]=b[1]+....+b[i];(这个很好证的)。

假如区间[2,4]都加上2的话

a数组变为a[]={1,8,10,7,10}，b数组变为b={1,7,2,-3,3};

发现了没有，b数组只有b[2]和b[5]变了，因为区间[2,4]是同时加上2的,所以在区间内b[i]-b[i-1]是不变的.

所以对区间[x,y]进行修改,只用修改b[x]与b[y+1]:

b[x]=b[x]+k;b[y+1]=b[y+1]-k;

所以，我们在存的时候就存差分数组，然后我们只改变l，与r+1的值，就好了。

那么单点查询呢？别忘了树状数组存的是前缀和！我们直接sum（a）。

那差分下的区间查询呢？直接原数列a[r]-a[l-1]！

二.二维树状数组

二维树状数组，就是矩阵嘛！你按照矩阵的方式做不就好了！

在add和sum函数里，两层循环，一层y一层x，不就好了！

然后就是二位树状数组所有的代码演示

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
int a[2000][2000],n;
int lowbit(int k)
{
    return k&(-k);
}
void change(int i,int y)
{
    int j;
    while(i<=n)
    {
        j=y;
        while(j<=n)
        {
            a[i][j]++;
            j+=lowbit(j);
        }
        i+=lowbit(i);
    }
}
int ask(int i,int y)
{
    int ans=0;
    int j;
    while(i!=0)
    {
        j=y;
        while(j!=0)
        {
            ans+=a[i][j];
            j-=lowbit(j);
        }
        i-=lowbit(i);
    }
    return ans;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        memset(a,0,sizeof(a));
        int m;
        scanf("%d%d",&n,&m);
        while(m--)
        {
            char opt;
            cin >> opt;
            if(opt==‘C‘)
            {
                int x1,x2,y1,y2;
                scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
                change(x2+1,y2+1);
                change(x1,y1);
                change(x1,y2+1);
                change(x2+1,y1);
            }
            else
            {
                int x,y;
                scanf("%d%d",&x,&y);
                printf("%d
",ask(x,y)&1);
            }
        }
        printf("
");
    }
}

二维树状数组