第十二章 圆周率的计算问题分析

Posted 2020-12-29 chy8

我们学习编程的最终目的就是解决问题：那我们试试看能不能用我们已学的知识解决圆周率的计算问题

方案一：公式法

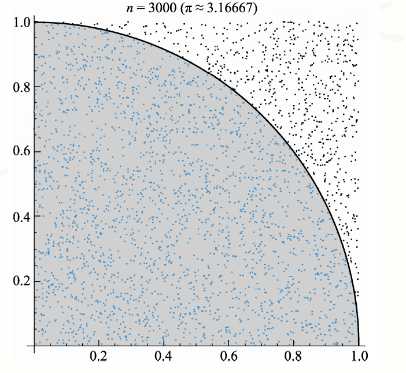
方案二：蒙特卡罗方法（撒点法）

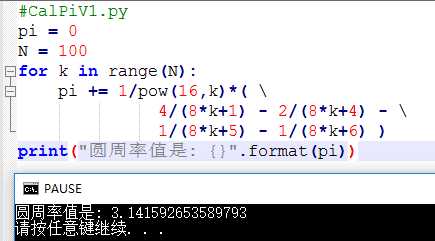
首先我们用方案一的方法进行尝试解决，代码如下：

1 #CalPiV1.py
2 pi = 0
3 N = 100
4 for k in range(N):
5     pi += 1/pow(16,k)*( 6               4/(8*k+1) - 2/(8*k+4) - 7               1/(8*k+5) - 1/(8*k+6) ) 
8 print("圆周率值是: {}".format(pi))

运行结果如下图所示：

下面我们使用蒙特卡罗方法计算圆周率大小

中心思想就是我们在一块如图的区域撒点，由面积比很容易得出，π是4倍的(在四分之一园内的点数除以总点数)

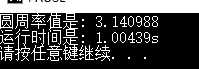
 1 #CalPiV2.py
 2 from random import random
 3 from time import perf_counter
 4 DARTS = 1000*1000 #一共的点数
 5 hits = 0.0　　#四分之一圆内的点数
 6 start = perf_counter()
 7 for i in range(1, DARTS+1):
 8     x, y = random(), random()
 9     dist = pow(x ** 2 + y ** 2, 0.5)　　#距离圆心的距离
10     if dist <= 1.0:
11         hits = hits + 1
12 pi = 4 * (hits/DARTS)
13 print("圆周率值是: {}".format(pi))
14 print("运行时间是: {:.5f}s".format(perf_counter() - start))

当然点数越多，结果越准确

运行结果如下