[POJ1179]Polygon

Posted 2020-12-29 si-rui-yang

http://poj.org/problem?id=1179

多边形是一个玩家在一个有n个顶点的多边形上的游戏，如图所示，其中n＝4。每个顶点用整数标记，每个边用符号+（加）或符号*（乘积）标记。

 

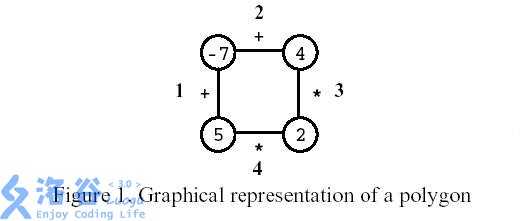
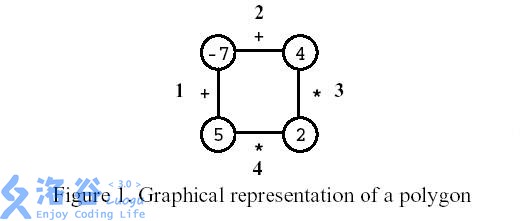
第一步，删除其中一条边。随后每一步：

选择一条边连接的两个顶点V1和V2，用边上的运算符计算V1和V2得到的结果来替换这两个顶点。

游戏结束时，只有一个顶点，没有多余的边。

如图所示，玩家先移除编号为3的边。之后，玩家选择计算编号为1的边，然后计算编号为4的边，最后，计算编号为2的边。结果是0。

 

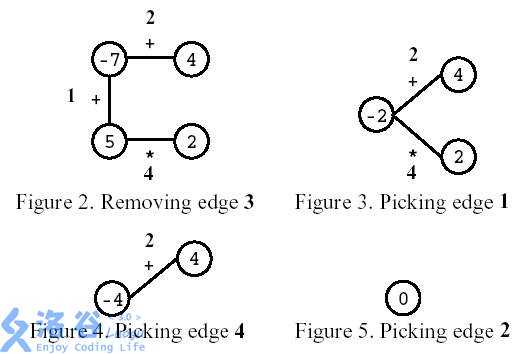
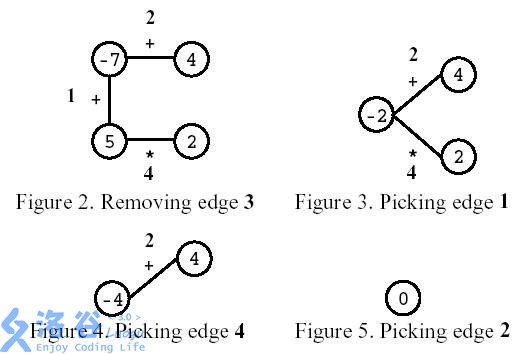
（翻译者友情提示：这里每条边的运算符旁边的数字为边的编号，不拿来计算）

编写一个程序，给定一个多边形，计算最高可能的分数。

输入格式

输入描述一个有n个顶点的多边形，它包含两行。第一行是数字n，为总边数。

第二行描述这个多边形，一共有2n个读入，每两个读入中第一个是字符，第二个是数字。

第一个字符为第一条边的计算符号(t代表相加，x代表相乘)，第二个代表顶点上的数字。首尾相连。

3 < = n < = 50

对于任何一系列的操作，顶点数字都在[-32768,32767]的范围内。

输出格式

第一行，输出最高的分数。在第二行，它必须写出所有可能的被清除后的边仍能得到最高得分的列表，必须严格递增。

Sample Input

4
t -7 t 4 x 2 x 5

Sample Output

33
1 2

Source

IOI 1998

 

一道区间dp题，先将环拆成链，再去枚举若拆掉第i条边所得到的最大值

显然，不仅仅要去求i,j区间里的最大值，还要求最小值，因为最小值有可能负数*负数得到一个很大的正数

dp方程见代码

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<cstdio>
using namespace std;
long long dp[101][101][2];
inline long long read()
{
    long long f=1,ans=0;char c;
    while(c<‘0‘||c>‘9‘){if(c==‘-‘)f=-1;c=getchar();}
    while(c>=‘0‘&&c<=‘9‘){ans=ans*10+c-‘0‘;c=getchar();}
    return f*ans;
}
long long n;
char strr;
long long a[101];
char st[101];
long long inf=2<<30-1;
void init()
{
    
    for(long long i=1;i<=n;i++)
        for(long long j=1;j<=n;j++) dp[i][j][1]=inf,dp[i][j][0]=-inf;
}
long long cx(long long a,long long b,char xx)
{
    if(xx==‘*‘) return a*b;
    return a+b;
}long long sz[101];char str[101];
long long dp_sry()
{
    for(long long k=1;k<n;k++)
        {
            for(long long i=1;i<=n&&i+k<=n;i++)
            {
                long long j=i+k;
                for(long long t=i;t<j;t++)
                {
//                    cout<<" i:"<<i<<"  j:"<<j<<"  t:"<<t<<endl;
//                    system("pause");
//                    cout<<cx(dp[i][t][0],dp[t+1][j][0],str[t])<<" "<<cx(dp[i][t][0],dp[t+1][j][1],str[t])<<" "<<cx(dp[i][t][1],dp[t+1][j][0],str[t])<<" "<<cx(dp[i][t][1],dp[t+1][j][1],str[t])<<" this is cx"<<endl;
                    dp[i][j][0]=max(dp[i][j][0],max(max(cx(dp[i][t][0],dp[t+1][j][0],str[t]),cx(dp[i][t][0],dp[t+1][j][1],str[t])),max(cx(dp[i][t][1],dp[t+1][j][0],str[t]),cx(dp[i][t][1],dp[t+1][j][1],str[t]))));
                    dp[i][j][1]=min(dp[i][j][1],min(min(cx(dp[i][t][0],dp[t+1][j][0],str[t]),cx(dp[i][t][0],dp[t+1][j][1],str[t])),min(cx(dp[i][t][1],dp[t+1][j][0],str[t]),cx(dp[i][t][1],dp[t+1][j][1],str[t]))));
//                    cout<<"dp:  "<<"i:"<<i<<"  j:"<<j<<"  "<<dp[i][j][0]<<" "<<dp[i][j][1]<<endl;
                }
                
            }
        }
        return max(dp[1][n][0],dp[1][n][1]);
}
long long sry[101];
int main()
{
    n=read();
    for(long long i=1;i<=n;i++)
    {
        cin>>strr>>a[i];
        a[i+n]=a[i];
        if(strr==‘t‘) st[i]=st[i+n]=‘+‘;
        else st[i]=st[i+n]=‘*‘;
    }
    long long maxn=-(2<<30-1),ans=0;
    for(long long i=1;i<=n;i++)
    {
        init();
        long long cnt=0;
        for(long long j=i;j<=i+n-1;j++) sz[++cnt]=a[j];
        cnt=0;
        for(long long j=i+1;j<=i+n-1;j++) str[++cnt]=st[j];
        for(long long j=1;j<=n;j++) dp[j][j][0]=dp[j][j][1]=sz[j];
        long long xx=dp_sry();
        if(xx==maxn) sry[++ans]=i;
        else if(xx>maxn) maxn=xx,ans=0,sry[++ans]=i;
    }
    cout<<maxn<<endl;
    for(long long i=1;i<ans;i++) cout<<sry[i]<<" ";cout<<sry[ans];
}

View Code