POJ 1177Picture 扫描线(若干矩形叠加后周长)
Posted weimeiyuer
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了POJ 1177Picture 扫描线(若干矩形叠加后周长)相关的知识,希望对你有一定的参考价值。
Picture
Description
A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.
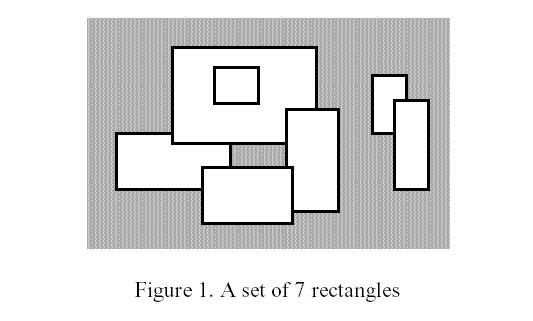
The corresponding boundary is the whole set of line segments drawn in Figure 2.
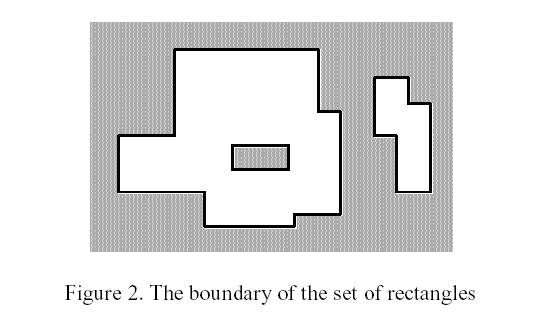
The vertices of all rectangles have integer coordinates.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.

The vertices of all rectangles have integer coordinates.
Input
Your
program is to read from standard input. The first line contains the
number of rectangles pasted on the wall. In each of the subsequent
lines, one can find the integer coordinates of the lower left vertex and
the upper right vertex of each rectangle. The values of those
coordinates are given as ordered pairs consisting of an x-coordinate
followed by a y-coordinate.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Output
Your
program is to write to standard output. The output must contain a
single line with a non-negative integer which corresponds to the
perimeter for the input rectangles.
Sample Input
7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16
Sample Output
228
题意
依次给出矩形左下角和右上角坐标,求若干矩形叠加后的周长。
解题思路
分别离散化x轴、y轴,然后做扫描线,一条扫x轴、一条扫y轴,累加即是周长。
//#include<bits/stdc++.h> #include<map> #include<set> #include<ctime> #include<cmath> #include<stack> #include<queue> #include<string> #include<vector> #include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> #include<algorithm> using namespace std; typedef long long ll; const int maxn=1e4+10; int cnt[maxn*4],n;//记录某个区间的下底边比上底边多的个数 double sum[maxn*4];//记录某个区间下底边比上底边多的个数总长度 double Hash[2][maxn];//对横坐标x离散化 struct node{ double l,r,h; int f; node(){} node(double x1,double x2,double hh,int ff):l(x1),r(x2),h(hh),f(ff){} bool operator<(const node &a)const{ return h<a.h; } }s[2][maxn*4]; void init(){ memset(sum,0,sizeof(sum)); memset(cnt,0,sizeof(cnt)); } void pushup(int x,int l,int r,int flag){ if(cnt[x]) sum[x]=Hash[flag][r+1]-Hash[flag][l];//表示该区间整个线段长度可作为底边 else if(l==r) sum[x]=0;//叶子结点区间长度为0,则底边长度为0 else sum[x]=sum[x*2]+sum[x*2+1]; } void update(int x,int flag,int L,int R,int val,int l,int r){ if(L<=l&&r<=R){ cnt[x]+=val; pushup(x,l,r,flag); return ; } int mid=(l+r)/2; if(L<=mid) update(x*2,flag,L,R,val,l,mid); if(R>mid) update(x*2+1,flag,L,R,val,mid+1,r); pushup(x,l,r,flag); } int main(){ double x1,x2,y1,y2; while(cin>>n&&n){ init();int k=0; while(n--){ scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2); if(x1>x2) swap(x1,x2); if(y1>y2) swap(y1,y2); Hash[0][k]=x1; Hash[1][k]=y1; s[0][k]=node(x1,x2,y1,1);s[1][k]=node(y1,y2,x1,1); k++; Hash[0][k]=x2; Hash[1][k]=y2; s[0][k]=node(x1,x2,y2,-1); s[1][k]=node(y1,y2,x2,-1); k++; } sort(s[0],s[0]+k);sort(s[1],s[1]+k);//把线段按高度h从小到大排序 sort(Hash[0],Hash[0]+k);sort(Hash[1],Hash[1]+k);//把x坐标从小到大排序 int ans1=unique(Hash[0],Hash[0]+k)-Hash[0];//去重复端点 int ans2=unique(Hash[1],Hash[1]+k)-Hash[1]; double SUM=0,last; init();last=0; for(int i=0;i<k;i++){ int l=lower_bound(Hash[0],Hash[0]+ans1,s[0][i].l)-Hash[0]; int r=lower_bound(Hash[0],Hash[0]+ans1,s[0][i].r)-Hash[0]; update(1,0,l,r-1,s[0][i].f,0,ans1-1); SUM+=abs(sum[1]-last); last=sum[1]; } init();last=0; for(int i=0;i<k;i++){ int l=lower_bound(Hash[1],Hash[1]+ans2,s[1][i].l)-Hash[1]; int r=lower_bound(Hash[1],Hash[1]+ans2,s[1][i].r)-Hash[1]; update(1,1,l,r-1,s[1][i].f,0,ans2-1); SUM+=abs(sum[1]-last); last=sum[1]; } printf("%d ",(int)SUM); } return 0; }
以上是关于POJ 1177Picture 扫描线(若干矩形叠加后周长)的主要内容,如果未能解决你的问题,请参考以下文章