算法导论——最小生成树

Posted 2020-12-28 graywind

　　对于一个连通图来说，我们可以去掉其中一些边依然保持其连通的性质，在这些图中存在一个或多个图，他们的路径总和是最小的，这样的图必然是树。因为，如果说图中存在环，则去掉环的一条边依然可以保证连通性，这与总路径和最小是矛盾的。这样的图被称为最下生成树。城市间铺设电路就可以利用最小生成树来进行规划。

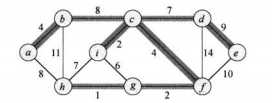
如图所示的黑色路径构成了最小生成树，去掉bc并加入ah也是一棵最小生成树，可见一个图的最小生成树并不一定是唯一的。

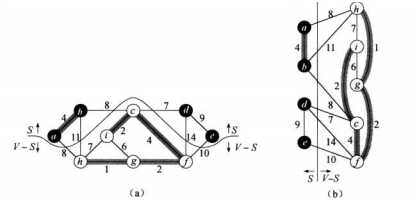
　　最小生成树可以使用安全边的策略进行生成：假设集合A是最小生成树的子集，我们可以找到一条边加入到A中，依然保持A是最小生成树的子集，这样的边就被称为安全边。为了寻找安全边，我们定义下方黑色部分ab与de边构成了集合A，(A,V-A)称为G的一个切割。如果一条边(v,u)一个端点属于A而另一个端点属于V-A，则称它为横跨切割(A,V-A)。在横跨切割的边中，可以找到一条或多条权重最小的边，该边称为轻量级边，轻量级边即是安全边。因为A一定要与V-A部分产生连接，这就必须要通过横跨切割的边，而轻量级边是其中最短的，所以必定属于最小生成树。下图所示ah bj bc cd df ef为横跨切割的边，其中cd为轻量级边。为了寻找轻量级边，有两种基于贪心策略的算法。

Kruskal算法

　　Kruskal算法的思想是，寻找连接森林中两棵不同树的边里面的最短边作为安全边加入集合A。可以使用不相交集合来维护这样的结构，对每个结点建立一棵树。通过FIND-SET来返回结点属于哪棵树，有边加入集合A时合并u和v所在的树。时间复杂度可表示为O(ElgV)。

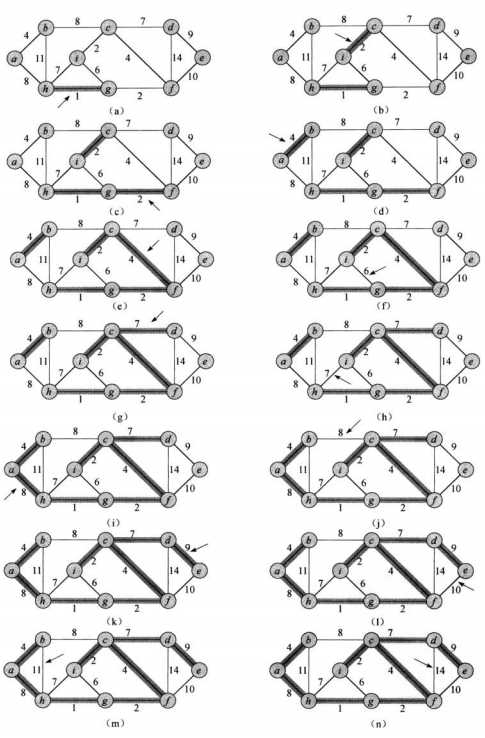
图中所示为各边按照长度顺序不断遍历检查是否要加入到集合A中，直到遍历完所有的边结束。

#include<stdio.h>
#include<vector>
#include <algorithm>
using namespace std;
#define SIZE 10

class Node{
public:
    int rank;
    Node *p;
};

class Road{
public:
    int u;
    int v;
    int weight;
};

int G[SIZE][SIZE];//邻接矩阵，参数初始化略
Node nodes[SIZE];

void makeSet(Node x){
    x.p = &x;
    x.rank = 0;
}

void Union(Node x,Node y){
    if(x.rank > y.rank)
        y.p = &x;
    else{
        x.p = &y;
        if(x.rank == y.rank)
            y.rank++;
    }
}

Node* findSet(Node x){
    if(x.p != &x)
        x.p = findSet(*x.p);
    return x.p;
}

bool com (Road a,Road b) {
    return (a.weight<b.weight); //升序排列
}

vector<Road> MSTKruskal(){
    vector<Road> A;
    int i,j;
    vector<Road> roads;
    for(i = 0; i < SIZE; i++){
        nodes[i] = *new Node();
        makeSet(nodes[i]);//每棵树包含一个结点
    }
    for(i = 0; i < SIZE; i++){
        for(j = i + 1; j < SIZE; j++){
            if(G[i][j] != 0){
                Road road = *new Road();
                road.u = i;
                road.v = j;
                road.weight = G[i][j];
                roads.push_back(road);
            }                
        }
    }
    sort(roads.begin(),roads.end(),com);//对所有路径进行降序排列
    for(i = 0; i < roads.size(); i++){
        Road road = roads[i];
        if(findSet(nodes[road.u]) != findSet(nodes[road.v])){
            A.push_back(road);
            Union(nodes[road.u],nodes[road.v]);
        }
    }
    return A;
}

Prim算法

　　Prim算法的思路是从根结点开始加入集合A，不断寻找A与V-A相连边中最短的，即横跨(A,V-A)的轻量级边。可以将V-A到A距离的最小值存储到优先队列Q中来减少每次遍历寻找最短边的时间。优先队列可以通过最小二叉堆或者斐波那契堆来实现，前者的渐进时间为O(ElgV)后者改进为O(E+VlgV）

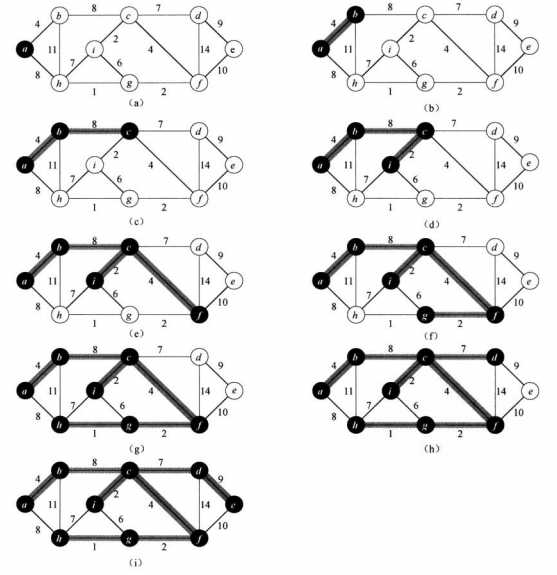
#include<stdio.h>
#include<vector>
using namespace std;
#define SIZE 10
#define INFI 10000

class Road{
public:
    int u;
    int v;
    int weight;
};

int G[SIZE][SIZE];//邻接矩阵，参数初始化略

vector<Road> MSTPrim(int root){
    vector<Road> A;
    int i;
    Road roads[SIZE];//记录到达A的最短路径
    for(i = 0; i < SIZE; i++){
        roads[i] = *new Road();
        if(G[root][i] != 0){
            roads[i].u = root;
            roads[i].v = i;
            roads[i].weight = G[root][i];
        }
        else
            roads[i].weight = INFI;
    }
    while(A.size() != SIZE - 1){
        int min = 0;
        for(i = 1; i < SIZE; i++){
            if(roads[i].weight < roads[min].weight && roads[i].weight > 0)
                min = i;//寻找最短的路径
        }
        A.push_back(roads[min]);
        roads[min].weight = -1;//表示该点已在A中
        for(i = 0; i < SIZE; i++){
            if(G[min][i] < roads[i].weight)
                roads[i].weight = G[min][i];//更新到达A的最短长度
        }
    }
    return A;
}