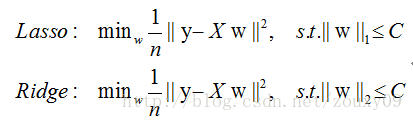L1与L2正则(转)

Posted 2020-12-28 demian

L0范数表示向量中非零元素的个数：NP问题，但可以用L1近似代替。

L1范数表示向量中每个元素绝对值的和：

 

L1范数的解通常是稀疏性的，倾向于选择数目较少的一些非常大的值或者数目较多的insignificant的小值。

L1和L2的差别，为什么一个让绝对值最小，一个让平方最小，会有那么大的差别呢？我看到的有两种几何上直观的解析：

1）下降速度：

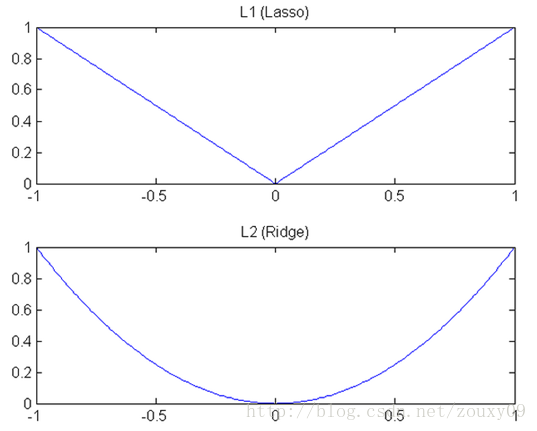
       我们知道，L1和L2都是规则化的方式，我们将权值参数以L1或者L2的方式放到代价函数里面去。然后模型就会尝试去最小化这些权值参数。而这个最小化就像一个下坡的过程，L1和L2的差别就在于这个“坡”不同，如下图：L1就是按绝对值函数的“坡”下降的，而L2是按二次函数的“坡”下降。所以实际上在0附近根据其梯度，L1的下降速度比L2的下降速度要快。

       L1在江湖上人称Lasso，L2人称Ridge。

2）模型空间的限制：

       实际上，对于L1和L2规则化的代价函数来说，我们可以写成以下形式：

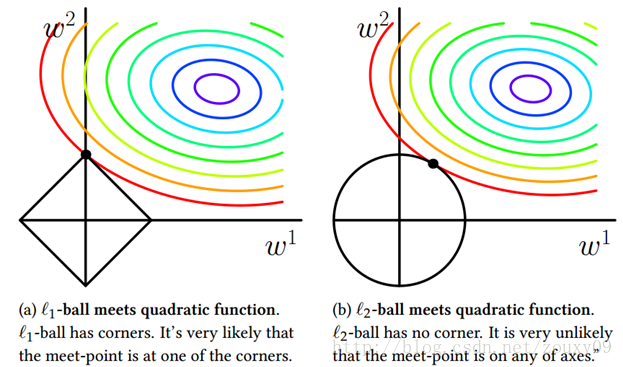
       也就是说，我们将模型空间限制在w的一个L1-ball 中。为了便于可视化，我们考虑两维的情况，在(w1, w2)平面上可以画出目标函数的等高线(凸函数3维空间里像一口锅)，而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解：

       可以看到，L1-ball 与L2-ball 的不同就在于L1在和每个坐标轴相交的地方都有“角”出现，而目标函数的测地线除非位置摆得非常好，大部分时候都会在角的地方相交。注意到在角的位置就会产生稀疏性，例如图中的相交点就有w1=0，而更高维的时候（想象一下三维的L1-ball 是什么样的？）除了角点以外，还有很多边的轮廓也是既有很大的概率成为第一次相交的地方，又会产生稀疏性。

       相比之下，L2-ball 就没有这样的性质，因为没有角，所以第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小了。这就从直观上来解释了为什么L1-regularization 能产生稀疏性，而L2-regularization 不行的原因了。

       因此，一句话总结就是：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。Lasso在特征选择时候非常有用，而Ridge就只是一种规则化而已。

转自：zouxy09