十动态规划
Posted jxkun
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了十动态规划相关的知识,希望对你有一定的参考价值。
目录
动态规划
12.1 动态规划方法关键点:
最优化原理, 也就是最优子结构性质, 这指的是最优化策略具有这样的性质, 不论过去状态和决策如何, 对前面的决策所形成的的状态而言, 余下的诸决策必须构成最优决策, 简单来说就是一个最优化决策略的子决策略总是最优子结构
无后效性, 指的是某状态下决策的收益, 只与状态和决策相关, 与到达该状态方式无关
子问题的重叠性, 动态规划将原来具有指数级时间复杂的暴力搜索算法改进成了具有多项式时间复杂度的算法, 其中的关键在于解决冗余, 这是动态规划算法的根本目的;
12.2 找零钱问题
题目: 有数组penny,penny中所有的值都为正数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个整数aim(小于等于1000)代表要找的钱数,求换钱有多少种方法。
给定数组penny及它的大小(小于等于50),同时给定一个整数aim,请返回有多少种方法可以凑成aim。
测试样例:
[1,2,4],3,3
返回:2解法
暴力穷举 -> 记忆法 -> 动态规划
- 暴力穷举法
如上例子: 取0张1元的时返回方法数r1, 取1张1元的时返回方法数r2, 取2张1元时方法数r3, 取3张1元时返回方法数r4, 累加即为 所有方法数;
而取0张1元时, 剩余可选2, 4, 逻辑相似, 递归求解;
import java.util.*;
public class Exchange {
public int countWays(int[] penny, int n, int aim) {
if(penny == null || penny.length == 0){
return 0;
}
return process1(penny, 0, aim);
}
public int process1(int[] arr, int index, int aim){
int res = 0;
if(index == arr.length){
res = aim == 0 ? 1 : 0;
}else{
for(int i = 0; arr[index]*i <= aim; i++){
res += process1(arr, index+1, aim - arr[index]*i);
}
}
return res;
}
}- 记忆搜索法
使用一个hash表, 存储参数为index, aim时的返回值, 等到下次index, aim相同时, 直接返回, 可以减少空间复杂度;
用空间换取时间;
import java.util.*;
public class Exchange {
public int countWays(int[] penny, int n, int aim) {
// write code here
if(penny == null || penny.length == 0 || aim < 0){
return 0;
}
int[][] map = new int[n+1][aim+1];
return process2(penny, 0, aim, map);
}
public int process2(int arr[], int index, int aim, int[][] map){
int res = 0;
if(index == arr.length){
res = aim == 0 ? 1 : 0;
}else {
for(int i = 0; arr[index]*i <= aim; i++){
int tmp = map[index + 1][aim - arr[index]*i];
if(tmp !=0){
res += tmp == -1 ? 0 : tmp;
}else{
res += process2(arr, index + 1, aim - arr[index]*i, map);
}
}
}
map[index][aim] = res == 0 ? -1 : res;
return res;
}
}动态规划法
申请n x (aim+1)大小的二维数组, 第一行, 只是用第一种货币, 记录组成0-aim之间钱数的方法数; 然后计算下一行...
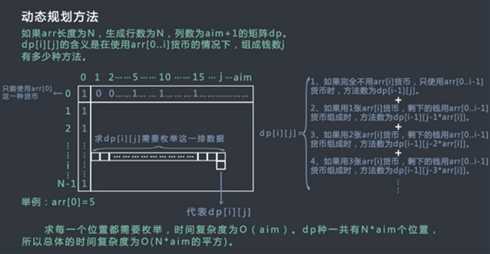
import java.util.*;
public class Exchange {
public int countWays(int[] penny, int n, int aim) {
// write code here
if(penny == null || penny.length == 0 || aim < 0){
return 0;
}
return process3(penny, n, aim);
}
public int process3(int arr[], int n, int aim){
int[][] tmp = new int[n][aim+1];
for(int i = 0; i <= aim; i++){
tmp[0][i] = i % arr[0] == 0 ? 1 : 0;
}
for(int i = 1; i < n; i++){
for(int j = 0; j <= aim; j++){
if(arr[i] > j){
tmp[i][j] = tmp[i-1][j];
}else{
tmp[i][j] = tmp[i][j - arr[i]] + tmp[i - 1][j];
}
}
}
return tmp[n - 1][aim];
}
}12.4 矩阵最小路径和
问题: 有一个矩阵map,它每个格子有一个权值。从左上角的格子开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,返回所有的路径中最小的路径和。
给定一个矩阵map及它的行数n和列数m,请返回最小路径和。保证行列数均小于等于100.
测试样例:
[[1,2,3],[1,1,1]],2,3
返回:4解法
经典动态规划题, 动态规划基本思路, 通过空间换取时间, 通过初始的数据递推出后面的值;
- 建立一个n×m的hash表存储从左上角到当前格子走的最小路径;
- 初始可知数据, 从左上角到达第一行的格子最小路径, 等于第一行格子的累加; 左上角到达第一列的格子的最小路径等于第一列格子的累加;
- 左上角到map[i][j]处的的最小路径为 tmp[i-1][j] + map[i][j] 与 tmp[i][j-1] + map[i][j]中更小的那个值;
import java.util.*;
public class MinimumPath {
public int getMin(int[][] map, int n, int m) {
if(n < 1 || m < 1){
return 0;
}
// write code here
int[][] dp = new int[n][m];
dp[0][0] = map[0][0];
for(int i = 1; i < n; i++){
dp[i][0] = dp[i-1][0] + map[i][0];
}
for(int i = 1; i < m; i++){
dp[0][i] = dp[0][i - 1] + map[0][i];
}
for(int i = 1; i < n; i++){
for(int j = 1; j < m; j++){
dp[i][j] = map[i][j] + (dp[i][j-1] > dp[i-1][j] ? dp[i-1][j] : dp[i][j-1]);
}
}
return dp[n-1][m-1];
}
}12.5 LIS(最长上升子序列)
问题: 这是一个经典的LIS(即最长上升子序列)问题,请设计一个尽量优的解法求出序列的最长上升子序列的长度。
给定一个序列A及它的长度n(长度小于等于500),请返回LIS的长度。
测试样例:
[1,4,2,5,3],5
返回:3解决
动态规划, 思路:
建立一个长度与A长度n对应长度的数组dp, 用于存储序列A中以每个元素为最长子序列末尾节点时的长度;
索引为0处, dp[0] = 1; 索引为i处 dp[i] = 1 + 索引i之前中比A[i]小的数中最大的dp值
根据递推关系, 可以很容易写出代码
import java.util.*;
public class LongestIncreasingSubsequence {
public int getLIS(int[] A, int n) {
// write code here
if(A == null || n == 0) return 0;
int[] dp = new int[n];
for(int i = 0; i < n; i++){
int max = 0;
for(int j = 0; j < i; j++){
if(A[j] < A[i]){
max = Math.max(max, dp[j]);
}
}
dp[i] = max + 1;
}
int res = -1;
for(int i = 0; i < n; i++){
res = Math.max(res, dp[i]);
}
return res;
}
}12.6 LCS
问题: 给定两个字符串A和B,返回两个字符串的最长公共子序列的长度。例如,A="1A2C3D4B56”,B="B1D23CA45B6A”,”123456"或者"12C4B6"都是最长公共子序列。
给定两个字符串A和B,同时给定两个串的长度n和m,请返回最长公共子序列的长度。保证两串长度均小于等于300。
测试样例:
"1A2C3D4B56",10,"B1D23CA45B6A",12
返回:6解决:
动态规划求解:
- 创建n×m的dp二维数组, dp[i][j] 表示A长度为i, B长度为j时的最大公共子序列
- 初始数据, 第一行n=0时, 若A[0] == B[j], 则dp[0][j] 及dp[0][j之后的索引] 值为1; 第一列m=0时, 若A[i] == B[0], 则dp[i][0] 及dp[i之后索引][0]值为1;
- 分两种情况
- A[i] == B[j] 则 dp[i][j] = dp[i-1][j-1] + 1
- A[i] != B[j] 则 dp[i][j] = Math.max(dp[i][j-1], dp[i-1][j])
代码实现如下:
public class LCS {
public int findLCS(String A, int n, String B, int m) {
// write code here
if(n == 0 || m == 0) return 0;
int[][] dp = new int[n][m];
dp[0][0] = A.charAt(0) == B.charAt(0) ? 1 : 0;
for(int i = 1; i < m; i++){
if(dp[0][i - 1] == 0){
dp[0][i] = dp[0][i - 1] + (A.charAt(0) == B.charAt(i) ? 1 : 0);
}else{
dp[0][i] = dp[0][i - 1];
}
}
for(int i = 1; i < n; i++){
if(dp[i - 1][0] == 0){
dp[i][0] = dp[i - 1][0] + (A.charAt(i) == B.charAt(0) ? 1 : 0);
}else{
dp[i][0] = dp[i-1][0];
}
}
for(int i = 1; i < n; i++){
for(int j = 1; j < m; j++){
if(A.charAt(i) == B.charAt(j)){
dp[i][j] = dp[i - 1][j - 1] + 1;
}else{
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
}
}
}
return dp[n-1][m-1];
}
}代码简化, 创建一个(n+1)×(m+1)的二维数组;
import java.util.*;
public class LCS {
public int findLCS(String A, int n, String B, int m) {
// write code here
if(n == 0 || m == 0) return 0;
int[][] dp = new int[n + 1][m+ 1];
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
if(A.charAt(i - 1) == B.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1] + 1;
}else{
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
}
}
}
return dp[n][m];
}
}12.8 01背包问题
问题 一个背包有一定的承重cap,有N件物品,每件都有自己的价值,记录在数组v中,也都有自己的重量,记录在数组w中,每件物品只能选择要装入背包还是不装入背包,要求在不超过背包承重的前提下,选出物品的总价值最大。
给定物品的重量w价值v及物品数n和承重cap。请返回最大总价值。
测试样例:
[1,2,3],[1,2,3],3,6
返回:6解决
方法一:
- 定义一个长度为cap+1长度的dp数组, 存储每个容量所能获取的最大价值
- dp[j] 的最大价值为 上一次的dp[j] 与 dp[j-w[i]] + v[i] 中的最大值
public class Backpack {
public int maxValue(int[] w, int[] v, int n, int cap) {
// write code here
int dp[] = new int[cap + 1];
for(int i = 0; i < n; i++ ){
for(int j = cap; j >= w[i]; j--){
dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);
}
}
return dp[cap];
}
}方法二:
- 创建二维数组存储
public class Backpack {
public int maxValue(int[] w, int[] v, int n, int cap) {
// write code here
int[][] dp = new int[n+1][cap+1];
for(int i = 1; i <= n; i++){
for(int j = 1; j <= cap; j++){
dp[i][j] = dp[i-1][j];
if(j >= w[i-1]){
dp[i][j] = Math.max(dp[i][j], dp[i-1][j - w[i-1]] + v[i-1]);
}
}
}
return dp[n][cap];
}
}12.9 最优编辑
问题: 对于两个字符串A和B,我们需要进行插入、删除和修改操作将A串变为B串,定义c0,c1,c2分别为三种操作的代价,请设计一个高效算法,求出将A串变为B串所需要的最少代价。
给定两个字符串A和B,及它们的长度和三种操作代价,请返回将A串变为B串所需要的最小代价。保证两串长度均小于等于300,且三种代价值均小于等于100。
测试样例:
"abc",3,"adc",3,5,3,100
返回:8解决


利用动态规划, 基本思路如下:
构建一个(n+1)×(m+1)的dp二维数组, dp[i][j] 表示长为i的字符串A转换成长为j的字符串B所需最小代价
初始化 dp[0][j] 和 dp[i][0] , dp[0][j] 的初始化, 0 -> j, 每次插入一个字符串; dp[i][0]的初始化, i -> 0, 每次删除一个字符串;
dp[i][j] 的值可能来自于 dp[i-1][j-1] 、 dp[i-1][j] 、 dp[i][j-1] 这三个地方, 取其中的最小值;计算如下:
- 若A.charAt[i-1] == B.charAt[j-1], 则dp[i][j] = dp[i-1][j-1] 否则dp[i][j] = dp[i-1][j-1] + c2
- dp[i][j] = dp[i-1][j] + c1; 即删除掉一个字符
- dp[i][j] = dp[i][j-1] + c0; 即插入一个字符
import java.util.*;
public class MinCost {
public int findMinCost(String A, int n, String B, int m, int c0, int c1, int c2) {
// write code here
int[][] dp = new int[n+1][m+1];
for(int i = 1; i <=n; i++){
dp[i][0] = c1*i;
}
for(int i = 0; i <= m; i++){
dp[0][i] = c0*i;
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
if(A.charAt(i - 1) == B.charAt(j - 1)){
dp[i][j] = Math.min(dp[i-1][j-1], Math.min(dp[i][j-1] + c0, dp[i-1][j] + c1));
}else{
dp[i][j] = Math.min(dp[i-1][j-1]+c2, Math.min(dp[i][j-1] + c0, dp[i-1][j]+c1) );
}
}
}
return dp[n][m];
}
}以上是关于十动态规划的主要内容,如果未能解决你的问题,请参考以下文章