关于课堂动手动脑以及课后实验性的问题的总结整理

Posted 2020-10-09

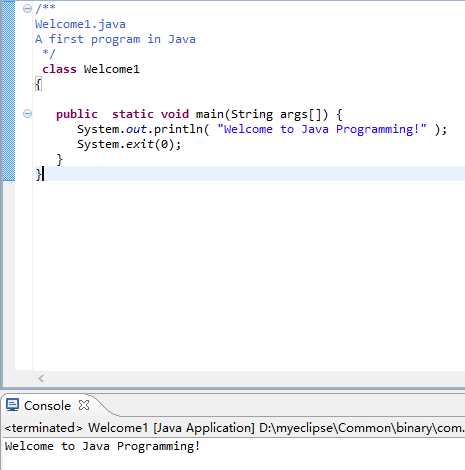
1.Welcome1.java

验证结果截图：

 

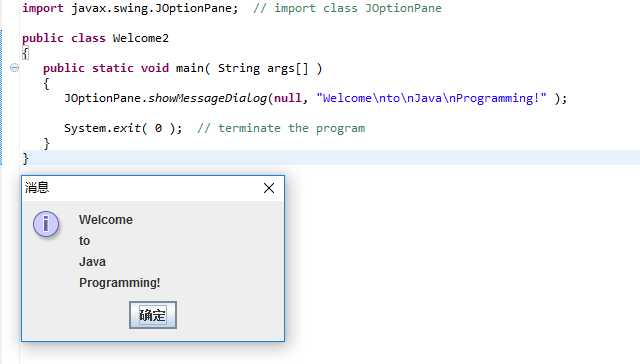
2.Welcome2.java

验证结果截图：

 

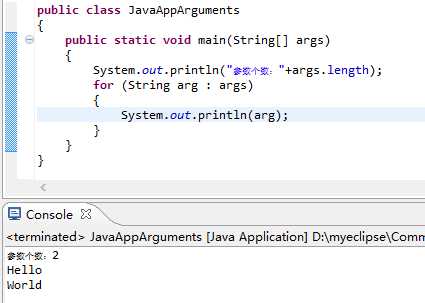
3.JavaAppArguments.java

验证结果截图：

 

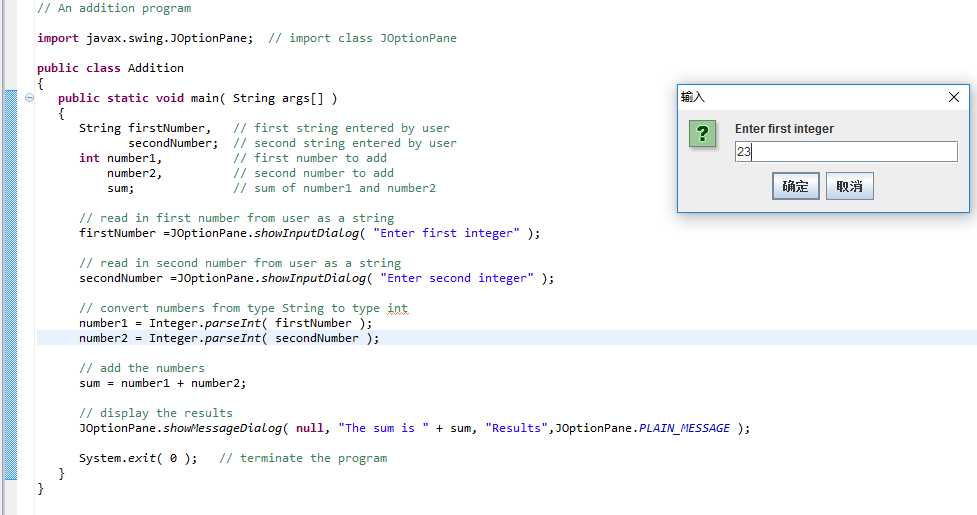
4.Addition.java

验证结果截图：

 

5.TestDouble.java

验证结果截图：

 

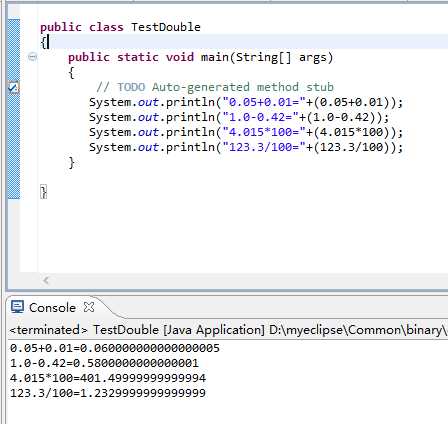
问题:为什么double类型的数值进行运算得不到“数学上精确”的结果？

 

十进制数的二进制表示可能不够精确

浮点数或是双精度浮点数无法精确表示的情况并不少见。浮点数值没办法用十进制来精确表示的原因要归咎于CPU表示浮点数的方法。这样的话您就可能会牺牲一些精度，有些浮点数运算也会引入误差。以上面提到的情况为例，2.4的二进制表示并非就是精确的2.4。反而最为接近的二进制表示是 2.3999999999999999。原因在于浮点数由两部分组成：指数和尾数。浮点数的值实际上是由一个特定的数学公式计算得到的。您所遇到的精度损失会在任何操作系统和编程环境中遇到。

计算机表示浮点数的方法：

s 符号位
M  表示有效数字，大于1小于2.
2^E 表示指数位。


例子：十进制的9，转化成二进制：1001.0，用二进制的科学表示法表示：1.001 * 2^3,此时s=0,
M=1.001,2^E=2^3,E= 3;
在32为的处理机中，1位表示符号位，8位表示指数位，23位表示有效数字位。我们知道科学技术法中E存在负数的情况（10 ^ -3） 所以E必须拿出一半的表示值来表示负数。
E为8位，它的取值范围为0-255；所以这个中间值就是127，他相当于0的作用。
对于上个例子 E=3 ,E+中间值=3 + 127 = 130； 130的二进制表示：10000010。有效数字计算机擦去省略第一个1的策略来存储。

6.TestBigDecimal

验证结果截图：

 

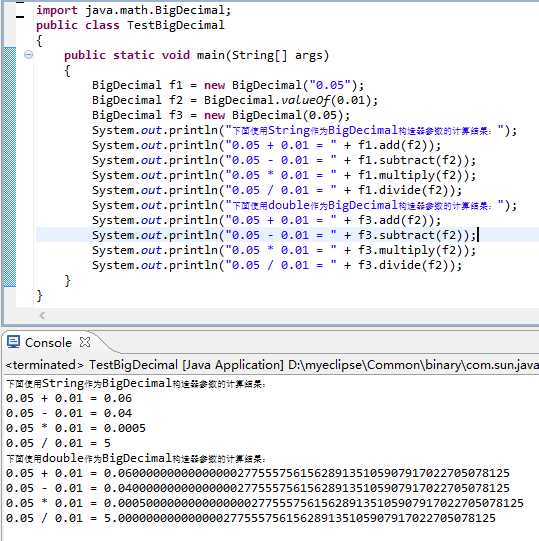
7.Verify

验证结果截图：

 

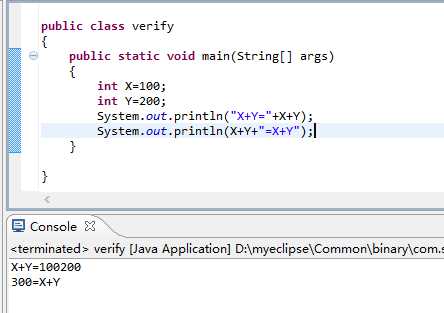
原因：

    对于第一个输出，源程序直接就按部就班执行输出x,y的值，对于第二个，源程序直接将x+y计算输出，再输出要输出的结果。