hdu 4565

Posted 2020-12-27 tingtin

Problem Description

　　A sequence S_n is defined as:

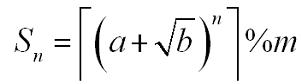
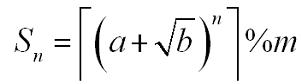
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S_n.
　　You, a top coder, say: So easy! 

 

 

Input

　　There are several test cases, each test case in one line contains four positive integers: a, b, n, m. Where 0< a, m < 2¹⁵, (a-1)²< b < a², 0 < b, n < 2³¹.The input will finish with the end of file.

 

 

Output

　　For each the case, output an integer S_n.

 

 

Sample Input

2 3 1 2013 2 3 2 2013 2 2 1 2013

 

 

Sample Output

4 14 4

 

 

1 (a+sqrt(b)）^n向上取整%M
2 令A(n)=(a+sqrt(b))^n,B(n)=(a-sqrt(b))^n
3 易得C(n)=A(n)+B(n)为整数
4 例如：2.3+0.7 ，由于（a-1)^2<b<a^2,因此B(n)为小于1的小数
5 那么A(n)向上取整的结果就是C(n),题目也就是求C(n)%M

 

 

 

 

 

 

 

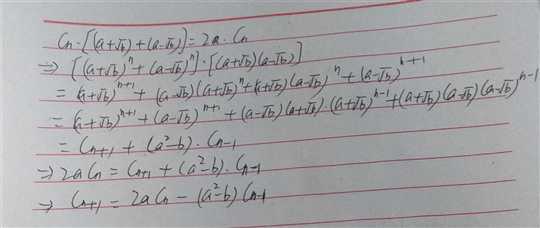
 1 #include <iostream>
 2 #include <cstring>
 3 #include <string>
 4 #include <queue>
 5 #include <set>
 6 #include <cmath>
 7 #include <cstdio>
 8 #include <algorithm>
 9 #include <cstdlib>
10 #define ll long long                          
11 #define max(x,y) (x>y?x:y)
12 #define min(x,y)  (x<y?x:y)
13 #define gep(i,a,b) for(ll i=a;i<=b;i++) 
14 using namespace std;
15 ll a,b,n,mod;
16 struct ma{
17     ll m[3][3];
18     ma(){
19         memset(m,0,sizeof(m));
20     }
21 };
22 ma qu(ma a,ma b,ll mod){
23     ma c;
24     gep(k,0,2){
25         gep(i,0,2){        
26                 if(a.m[i][k]){
27                     gep(j,0,2){
28                     c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j]%mod+mod)%mod;
29                     }
30             }
31         }
32     }
33     return c;
34 }
35 ma quick_qu(ma a,ll b,ll mod){
36     ma c;
37     gep(i,0,2){
38         c.m[i][i]=1ll;
39     }
40     while(b){
41         if(b&1) c=qu(c,a,mod);
42         b>>=1;
43         a=qu(a,a,mod);
44     }
45     return c;
46 }
47 int main()
48 {  
49     while(~scanf("%lld%lld%lld%lld",&a,&b,&n,&mod)){
50         if(n==1){
51             printf("%lld
",2*a%mod);
52             continue;
53         }
54          ma c;
55          c.m[0][0]=2*a;c.m[0][1]=b-a*a;
56          c.m[1][0]=1;c.m[2][1]=1;
57          ma d;
58          d.m[0][0]=2*a*a*a+6*a*b;d.m[1][0]=2*a*a+2*b;d.m[2][0]=2*a;
59          ma e=quick_qu(c,n-1,mod);
60          ma f;
61          f=qu(e,d,mod);     
62          printf("%lld
",f.m[2][0]);
63     }
64     return 0;
65 }