前向星与链式前向星

Posted 2020-12-27 wkfvawl

这里借鉴了一些大佬的文章和代码，给出链接，谢谢

https://blog.csdn.net/ACdreamers/article/details/16902023

https://blog.csdn.net/wuhuajunbao/article/details/22589619

引言

一般来讲，图的常用存储结构有邻接矩阵，和邻接表，但我们知道邻接矩阵是好写但效率低，邻接表虽效率高但不好写，今天来讲一下图的另一只常用的存储结构：前向星和链式前向星，介于上述两种存储结构之间的一种比较中庸的存储结构——前向星。前向星固然好些，但效率依旧并不高。而在优化为链式前向星后，效率也得到了较大的提升。虽然说，世界上对链式前向星的使用并不是很广泛，但在不愿意写复杂的邻接表的情况下，链式前向星也是一个很优秀的数据结构。

首先我们来说一下图的前向星表示方法：

 

1.前向星

前向星是一种通过存储边信息的方式来存储图的一种数据结构，他构造简单，读入每条边的信息，将边存放在数组中，把数组中的边按照起点顺序排列，前向星也就构造完成了。方便查询，我们用另外一个数组用head[i]记录以i为边集在数组中的第一个存储位置.

如图：

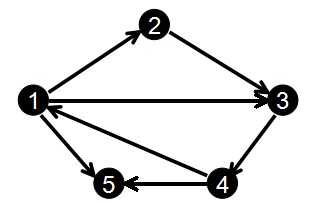
我们输入边的顺序为:

1 2

2 3

3 4

1 3

4 1

1 5

4 5

那么排完序后就得到:

编号:     1      2      3      4      5      6      7

起点u:    1      1      1      2      3      4      4

终点v:    2      3      5      3      4      1      5

得到:

head[1] = 1   

head[2] = 4   

head[3] = 5  

head[4] = 6

  

存储结构：

struct node
{
    int from;///起点
    int to;///终点
    int w;///权值
} edge[maxm];
int head[maxn];

比较函数：

bool cmp(node a,node b)
{
    if(a.from == b.from && a.to == b.to) return a.w < b.w;
    if(a.from == b.from) return a.to < b.to;
    return a.from < b.from;
}

读入数据：

void input()
{
    for(int i = 0; i < m; i ++)
    {
        scanf("%d%d%d",&edge[i].from,&edge[i].to,&edge[i].w);
    }
    memset(head ,-1 ,sizeof(head));
    sort(edge , edge + m , cmp);
    head[edge[0].from] = 0;
    for(int i = 1; i < m; i ++)
    {
        if(edge[i].from != edge[i-1].from)
        {
            head[edge[i].from] = i;   //确定起点为vi的第一条边的位置。
        }
    }
}

遍历数据：

void output()
{
    for(int i = 1; i <= n; i ++)
        cout << "head["<<i<<"]: "<<head[i]<<endl;
    cout << "遍历所有的边"<<endl;
    for(int i = 1; i <= n; i ++) //head[i]的下标i等于vi;
    {
        for(int j = head[i]; edge[i].from == i && j < m; j  ++)
        {
            cout << edge[j].from << " " << edge[j].to << " " << edge[j].w <<endl;
        }
    }
}

 完整代码：

 

 1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstdio>
 4 #include <cstring>
 5 using namespace std;
 6 const int maxn = 1000;
 7 const int maxm = 1000000;
 8 struct node
 9 {
10     int from;///起点
11     int to;///终点
12     int w;///权值
13 } edge[maxm];
14 int head[maxn];
15 int n,m ;
16 bool cmp(node a,node b)
17 {
18     if(a.from == b.from && a.to == b.to) return a.w < b.w;
19     if(a.from == b.from) return a.to < b.to;
20     return a.from < b.from;
21 }
22 void input()
23 {
24     for(int i = 0; i < m; i ++)
25     {
26         scanf("%d%d%d",&edge[i].from,&edge[i].to,&edge[i].w);
27     }
28     memset(head ,-1 ,sizeof(head));
29     sort(edge , edge + m , cmp);
30     head[edge[0].from] = 0;
31     for(int i = 1; i < m; i ++)
32     {
33         if(edge[i].from != edge[i-1].from)
34         {
35             head[edge[i].from] = i;   //确定起点为vi的第一条边的位置。
36         }
37     }
38 }
39 
40 void output()
41 {
42     for(int i = 1; i <= n; i ++)
43         cout << "head["<<i<<"]: "<<head[i]<<endl;
44     cout << "遍历所有的边"<<endl;
45     for(int i = 1; i <= n; i ++) //head[i]的下标i等于vi;
46     {
47         for(int j = head[i]; edge[i].from == i && j < m; j  ++)
48         {
49             cout << edge[j].from << " " << edge[j].to << " " << edge[j].w <<endl;
50         }
51     }
52 }
53 int main()
54 {
55     while(scanf("%d%d",&n , &m)!=EOF)
56     {
57         input();
58         output();
59     }
60     return 0;
61 }

View Code

 

可以看出，前向星构造时间的复杂度主要取决于排序函数，一般来说，时间复杂度为O（m logm）；空间上需要两个数组，故空间复杂度为O（m+n）；前向星的有点在于可以对应点非常多的情况，可以存储重复边，但不能直接判断图中任意两点是有边。

 2.链式前向星

 

 建立存储结构：

struct EDGE{
    int next;   //下一条边的存储下标
    int to;     //这条边的终点
    int w;      //权值
}edge[MAXM];

另外还有一个数组head[],它是用来表示以i为起点的第一条边存储的位置,实际上你会发现这里的第一条边存储的位置其实在以i为起点的所有边的最后输入的那个编号.

 

int head[MAXN];  //head[i]表示以i为起点的第一条边

 

head[]数组一般初始化为-1,对于加边的add函数是这样的:

 

void add(int u,int v,int w)
{
    edge[cnt].w = w;
    edge[cnt].to = v;
    edge[cnt].next = head[u];
    head[u] = cnt++;
}

 

初始化cnt = 0,这样,现在我们还是按照上面的图和输入来模拟一下:

 

 

 

 

edge[0].to = 2;     edge[0].next = -1;      head[1] = 0;

edge[1].to = 3;     edge[1].next = -1;      head[2] = 1;

edge[2].to = 4;     edge[2],next = -1;      head[3] = 2;

edge[3].to = 3;     edge[3].next = 0;       head[1] = 3;

edge[4].to = 1;     edge[4].next = -1;      head[4] = 4;

edge[5].to = 5;     edge[5].next = 3;       head[1] = 5;

edge[6].to = 5;     edge[6].next = 4;       head[4] = 6;

 

很明显,head[i]保存的是以i为起点的所有边中编号最大的那个,而把这个当作顶点i的第一条起始边的位置.

这样在遍历时是倒着遍历的,也就是说与输入顺序是相反的,不过这样不影响结果的正确性.

比如以上图为例,以节点1为起点的边有3条,它们的编号分别是0,3,5   而head[1] = 5

遍历数据：

for(int i=head[st]; i!=0; i=edge[i].next) 
    {///i开始为第一条边，每次指向下一条(以0为结束标志)若下标从0开始，next应初始化-1
        cout << "Start: " << st << endl;
        cout << "End: " << edge[i].to << endl;
        cout << "W: " << edge[i].w << endl << endl;
    }

那么就是说先遍历编号为5的边,也就是head[1],然后就是edge[5].next,也就是编号3的边,然后继续edge[3].next,也就是编号0的边,可以看出是逆序的.