CF1012B

Posted 2020-12-26 ullio

题目链接

题目描述

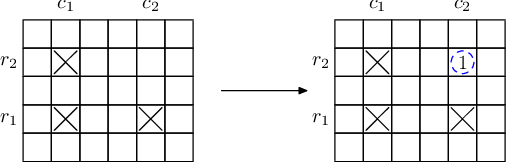
给你一幅(N ast M)的图,图中有一些点已经被选定.
你有两个选择:
1.花费1代价选择一个没有被选过的点.
2.花费0代价选择一个点(left(r_{2},c_{2} ight)),当且仅当点(left(r_{1},c_{2} ight), left(r_{2},c_{1} ight), left(r_{1},c_{1} ight))被选择.
问选择所有点的最小代价.

输入输出格式

输入格式:

第一行包含三个整数n,m,q,表示图的大小和已有的点的数量.
以下q行包含两个整数ri,ci,每个都描述了已经拥有的点,且保证输入中的所有点都不同.
(left(1 leq n,m leq 200000 ight))
(left(0 leq q leq min left( nast m,200000 ight) ight))
(left( 1 leq r_{i} leq n , 1 leq c_{i} leq m ight))

输出格式:

一个整数表示最小代价.

样例

输入样例	输出样例
2 2 3 1 2 2 2 2 1	0

略

思路

1.并查集

将原图抽象为N+M个点
对于一个存在的点(x,y),将bcj[x]与(bcj left[ y + N ight])合并
考虑选择一个点(left(r_{2},c_{2} ight))
当(left(r_{1},c_{2} ight), left(r_{2},c_{1} ight), left(r_{1},c_{1} ight))已被选择时
思考并查集的连接情况
........................................
((r_{1} , r_{2} , c_{1} , c_{2})的连通性)
........................................
会发现$ r_{2} , c_{2} $已经在一个联通块中
对于一个联通块来说,其内部的点都是可以互相构成的
整个图联通,其实就对应了原图所有点都被选择
那么先将0费的点按上述过程连接起来,就构成了0费时的联通块
而将两个联通块合一的代价是显而易见的
就是选择一个点的代价

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <queue>
#include <stack>
#include <list>
#include <set>
#include <map>
#define ll long long
#define ull unsigned long long
#define ci const int&
#define cl const long long&
#define cul const undigned long long&
#define io_f std::ios::sync_with_stdio(false)
using namespace std;

int n,m,q;
int bcj[400100];

int fd(ci x) {return x==bcj[x]?x:bcj[x]=fd(bcj[x]);}

int main() {
    io_f;
    int a,b;
    cin>>n>>m>>q;
    for(int i=1;i<=n+m;i++) bcj[i]=i;
    for(int i=1;i<=q;i++) {
        cin>>a>>b;
        bcj[fd(bcj[a])]=fd(bcj[b+n]);
    }
    int ans=0;
    for(int i=1;i<=n+m;i++)
        if(bcj[i]==i)ans++;
    cout<<ans-1<<endl;

    return 0;
}