杭电2018多校第一场(2018 Multi-University Training Contest 1) 1008.RMQ Similar Sequence (HDU6305) -笛卡尔树+数学期望

Posted 2020-12-26 zero-

 

 

6305.RMQ Similar Sequence

 

这个题的意思就是对于A，B两个序列，任意的l，r，如果RMQ(A，l，r)=RMQ(B，l，r)，B序列里的数为[0,1]的实数，B的重量为B的所有元素的和，否则为0。问你B的期望重量是多少。

dls讲题说是笛卡尔树，笛卡尔树是一种特定的二叉树数据结构，具体的看这篇博客吧：【pushing my way】笛卡尔树

这个题就是笛卡尔树同构的问题，假设A的笛卡尔树的子树大小为sz[u]，那么序列B与A同构的概率为，因为B中的数满足均匀分布(因为B中的元素为[0,1]中的任意实数)，所以每个位置的期望值为(0+1)/2，那么B的重量总和为n/2，所以B的重量的期望值为。

 

贴一下官方题解:

RMQ-Similar实际上就是A和B的笛卡尔树一样，这样我们就有了一个二叉树，然后可以在树上分析了。 考虑到B中有元素相同的概率是0，于是可以假设B里面元素互不相同，也就是说可以假定是一个排列。 显然，符合笛卡尔树的排列就是这个树的拓扑序列个数，就是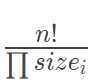。然后显然每个排列期望的和是，于是答案就是。

 

代码(参考别人的模板)：

 1 //1008-6305-RMQ的概念、笛卡尔树模板题，同构求bi的拓扑序个数
 2 #include<iostream>
 3 #include<cstdio>
 4 #include<cstring>
 5 #include<algorithm>
 6 #include<cmath>
 7 #include<cstdlib>
 8 #include<cassert>
 9 #include<queue>
10 #include<vector>
11 #include<stack>
12 using namespace std;
13 typedef long long ll;
14 const int maxn=1e6+10;
15 const int inf=0x3f3f3f3f;
16 const int mod=1e9+7;
17 
18 stack<int>st;
19 ll inv[maxn];
20 int n;
21 
22 struct node{
23     int val,sz;
24     int l,r,par;
25 }t[maxn];
26 
27 
28 void init()
29 {
30     for(int i=0;i<=n;i++)
31         t[i].l=0,t[i].r=0,t[i].par=0,t[i].sz=0;//初始化
32     t[0].val=inf;
33     while(!st.empty())
34         st.pop();
35     st.push(0);
36 }
37 
38 void build()
39 {
40     for(int i=1;i<=n;i++){
41         while(!st.empty()&&t[st.top()].val<t[i].val)//从栈顶往栈底遍历，
42             st.pop();
43         int par=st.top();
44         t[i].par=par;//i.par为st.pop()
45         t[i].l=t[par].r;
46         t[t[par].r].par=i;
47         t[par].r=i;//右子树
48         st.push(i);
49     }
50 }
51 
52 void dfs(int u)
53 {
54     if(u==0) return ;
55     t[u].sz=1;
56     dfs(t[u].l);
57     dfs(t[u].r);
58     t[u].sz+=t[t[u].l].sz+t[t[u].r].sz;
59 }
60 
61 void Inv(){//扩展gcd求逆元
62     inv[1]=1;
63     for(int i=2;i<maxn;i++)
64         inv[i]=inv[mod%i]*(mod-mod/i)%mod;
65 }
66 
67 int main()
68 {
69     int T;
70     Inv();
71     scanf("%d",&T);
72     while(T--){
73         scanf("%d",&n);
74         init();
75         for(int i=1;i<=n;i++)
76             scanf("%d",&t[i].val);
77         build();
78         dfs(t[0].r);
79 
80         ll ans=n*inv[2]%mod;
81         for(int i=1;i<=n;i++)
82             ans=ans*inv[t[i].sz]%mod;
83         printf("%lld
",ans);
84     }
85 }

 

 

代码(标程)：

 1 #include <cstdio>
 2 #include <functional>
 3 #include <algorithm>
 4 #include <vector>
 5 #include <queue>
 6 
 7 using int64 = long long;
 8 
 9 const int mod = 1e9 + 7;
10 
11 int main() {
12   int T;
13   scanf("%d", &T);
14   for (int cas = 1; cas <= T; ++cas) {
15     int n;
16     scanf("%d", &n);
17     std::vector<int> a(n);
18     for (int i = 0; i < n; ++i) {
19       scanf("%d", &a[i]);
20     }
21 
22     std::vector<int> left(n, -1), right(n, -1), stk(n), parent(n, -1);
23     for (int i = 0, top = 0; i < n; ++i) {
24       int last = -1;
25       while (top && a[i] > a[stk[top - 1]]) {
26         last = stk[--top];
27       }
28       if (top) {
29         right[stk[top - 1]] = i;
30         parent[i] = stk[top - 1];
31       }
32       left[i] = last;
33       if (last != -1) parent[last] = i;
34       stk[top++] = i;
35     }
36 
37     std::vector<int> inv(n + 2, 1);
38     for (int i = 2; i < n + 2; ++i) {
39       inv[i] = int64(mod - mod / i) * inv[mod % i] % mod;
40     }
41 
42     using pii = std::pair<int, int>;
43     {
44       std::vector<pii> a(n), b(n);
45       std::queue<int> queue;
46       std::vector<int> cnt(n);
47       for (int i = 0; i < n; ++i) {
48         a[i] = b[i] = {inv[2], 0};
49         if (left[i] == -1 && right[i] == -1) {
50           queue.push(i);
51         }
52         cnt[i] = (left[i] != -1) + (right[i] != -1);
53       }
54       while (!queue.empty()) {
55         int u = queue.front(); queue.pop();
56         pii res = {(int64)a[u].first * inv[a[u].second] % mod * b[u].first % mod * inv[b[u].second] * 2 % mod, a[u].second + b[u].second + 1};
57         int p = parent[u];
58         if (p == -1) {
59           printf("%d
", res.first);
60           break;
61         }
62         if (cnt[p] == 2) a[p] = res;
63         else if (cnt[p] == 1) b[p] = res;
64         --cnt[p];
65         if (cnt[p] == 0) queue.push(p);
66       }
67     }
68   }
69   return 0;
70 }

 

 

讲道理，还是有点不太清楚，还不熟练，多学习一下。

 

溜了。。。