[Luogu P1122]最大子树和 (简单树形DP)

Posted 2020-12-26 goldenpotato

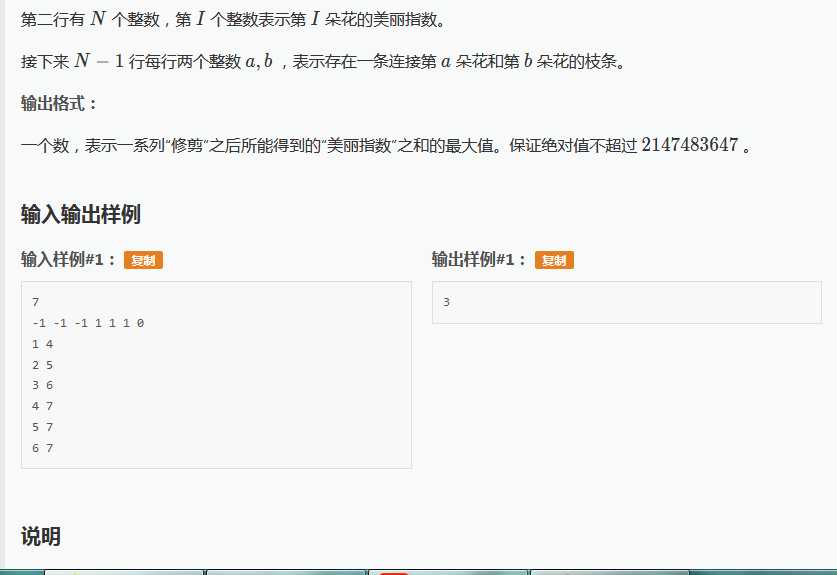
题面

传送门：https://www.luogu.org/problemnew/show/P1122

 

---

Solution

这是一道简单的树形DP题。

首先，我们可以转换一下题面，可以发现，题目要求我们求出一颗树上的最大联通子图。

因为我们是在树上取的，实际上就是取一颗子树。

这个就是最基础的树形DP模型了。

 

我们可以设f[i]表示我们选的子图以i为根所能取的子树的最大值。

转移是：

f[i] = beauty[i] + xigema(max(f[j],0))

（也就是一颗树的孩子所能取的子树，如果它孩子为根的子树>0，就取它，否则不取）

答案就是最大的f[i]

 

---

Code

//Luogu P1122 最大子树和
//Jul,30th,2018
//树形DP
#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c==‘-‘) f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-‘0‘;c=getchar();}
    return x*f;
}
const int N=16000+100;
const int inf=0x3f3f3f3f;
vector <int> e[N];
int n,beauty[N];
long long f[N];
bool vis[N];
long long dfs(int x)
{
    f[x]=beauty[x];
    vis[x]=true;
    for(int i=0;i<int(e[x].size());i++)
        if(vis[e[x][i]]==false)
            f[x]=max(f[x],f[x]+dfs(e[x][i]));
    return f[x];
}
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
        e[i].reserve(4);
    for(int i=1;i<=n;i++)
        beauty[i]=read();
    for(int i=1;i<n;i++)
    {
        int s=read(),t=read();
        e[s].push_back(t);
        e[t].push_back(s);
    }
    
    dfs(1);
    
    long long ans=-inf;
    for(int i=1;i<=n;i++)
        ans=max(ans,f[i]);
    printf("%lld",ans);
    return 0;
}

正解(C++)