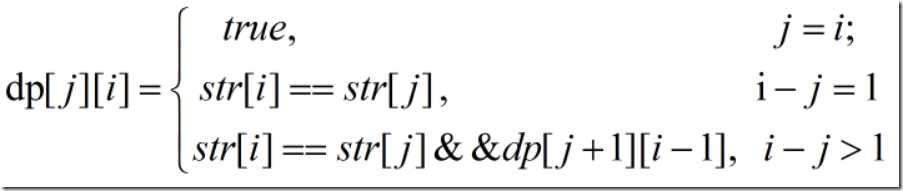最长回文子串 (动态规划法中心扩展算法)

Posted 2020-12-26 daleyzou

问题描述：

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。

思考：

嗯，回文嘛！就是顺序读取和逆序读取的结果是一样的，那我们可以使用两个for循环来不断的截取给定的字符串S，然后判断截取后的字符串是不是回文串，与此同时，使用一个新的字符串result来保存我们截取到的并且长度最长的回文串。

代码：

public String longestPalindrome_reconstructure1(String s){ // 超出时间限制
        if (s.length() < 2){
            return s;
        }
        String result = s.substring(0,1);
        String temp = null;
        String temp1 = null;
        for(int i = 0; i < s.length() - 1; i++){
            temp = null;
            temp1 = null;
            for (int j = s.length(); j > i; j--){
                if (j - i < result.length()) break;
                temp = s.substring(i, j);
                temp1 = new StringBuilder(temp).reverse().toString(); // 对截取后的字符串进行反转

                if (temp.equals(temp1) && temp.length() > result.length()){
                    result = temp;
                }
            }
        }
        return result;
    }

上述代码倒是完成了得到最长回文子串的功能，但是，有个很明显的缺点就是时间开销太大了，所以肯定得想想办法减小时间开销

使用中心扩展算法：

我们观察到回文中心的两侧互为镜像。因此，回文可以从它的中心展开，并且只有 2n - 1个这样的中心。

你可能会问，为什么会是 2n - 1 个，而不是 n个中心？原因在于所含字母数为偶数的回文的中心可以处于两字母之间（例如 ：“abba” 的中心在两个b之间），时间复杂度也只有O(n?2??)

代码：

// 使用中心扩展算法
    public String longestPalindrome_reconstructure2(String s) { // 第二次对代码进行重构
        if (s.length() < 2) { // 单个字符肯定是回文串，直接返回s
            return s;
        }
        int maxLength = 0;
        int center = 0;
        for (int i = 0; i < s.length(); i++){
            int begin = centerExpand(s, i, i);          // 最长回文串长度为奇数
            int end = centerExpand(s, i, i + 1);   // 最长回文串长度为偶数

            if (maxLength < Math.max(begin, end)){
                center = i;                                // 以center为中心
                maxLength = Math.max(begin, end);          // 最长回文串长度
            }
        }
        // 如果我们的回文串的长度为偶数，那么中心左边的长度会比右边的长度小1
        return s.substring(center - (maxLength - 1) / 2, center + maxLength / 2 + 1);
    }

    int centerExpand(String s, int begin, int end){
        int left = begin, right = end;
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)){
            left--;
            right++;
        }
        // 返回以begin,end为基准，同时向左向右扩展后能够得到的最长回文串长度
        return right - left - 1;
    }

使用动态规划法：

避免在验证回文时进行不必要的重复计算。考虑 “ababa” 这个示例。如果我们已经知道 “bab” 是回文，那么很明显，“ababa” 一定是回文，因为它的左首字母和右尾字母是相同的。

P(i,j)=(P(i+1,j?1) and S?i??==S?j??)

我们首先初始化一字母和二字母的回文，然后找到所有三字母回文，并依此类推…

代码：

// 使用动态规划法
    public String longestPalindrome_reconstructure3(String s) { // 第三次对代码进行重构
        if (s.length() < 2) { // 单个字符肯定是回文串，直接返回s
            return s;
        }
        boolean[][] dp = new boolean[s.length()][s.length()];  // 初始化一个二维数组，值默认是false
        String result = s.substring(0,1);
        for (int j = 0; j < s.length(); j++){
            for (int i = 0; i <= j; i++){
                dp[i][j] = s.charAt(i) == s.charAt(j) &&(j - i <= 2 || dp[i+1][j-1]);
                if (dp[i][j]){
                    if (j - i + 1 > result.length()){
                        result = s.substring(i, j + 1);
                    }
                }
            }
        }
        return result;
    }