Problem D. Euler Function

Posted 2020-12-26 longl

Problem D. Euler Function

题目：

 

Problem D. Euler Function

http://acm.hdu.edu.cn/showproblem.php?pid=6324

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 66    Accepted Submission(s): 64

Problem Description

In number theory, Euler‘s totient function φ(n) counts the positive integers up to a given integer n that are relatively prime to n. It can be defined more formally as the number of integers k in the range 1≤k≤n for which the greatest common divisor gcd(n,k) is equal to 1.
For example, φ(9)=6 because 1,2,4,5,7 and 8 are coprime with 9. As another example, φ(1)=1 since for n=1 the only integer in the range from 1 to nis 1 itself, and gcd(1,1)=1.
A composite number is a positive integer that can be formed by multiplying together two smaller positive integers. Equivalently, it is a positive integer that has at least one divisor other than 1 and itself. So obviously 1 and all prime numbers are not composite number.
In this problem, given integer k, your task is to find the k-th smallest positive integer n, that φ(n) is a composite number.

 

 

Input

The first line of the input contains an integer T(1≤T≤100000), denoting the number of test cases.
In each test case, there is only one integer k(1≤k≤109).

 

 

Output

For each test case, print a single line containing an integer, denoting the answer.

 

 

Sample Input

2 1 2

 

 

Sample Output

5 7

 

 

Source

2018 Multi-University Training Contest 3

 

 

题意：

　　给定k, 求第k小的数n, 满足 φ(n)是合数

 

思路

  　暴力打表后发现除了，φ(i) i=1..5,6 不是合数外，其余都是，因而 f(1)=5,  f(k)=k+5 (k>=2)

 

证明

 

 

 

 

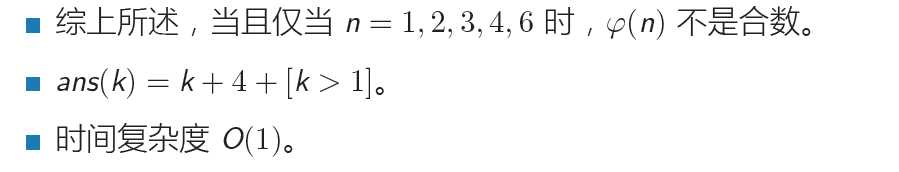
代码：

#include<stdio.h>int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        int n;
        scanf("%d",&n);
        if(n==1)printf("5
");
        else printf("%d
",n+5);
    }
    return 0;
}